Bài kiểm tra 1 tiết môn: Hình học – Chương II (nâng cao)
Đề:
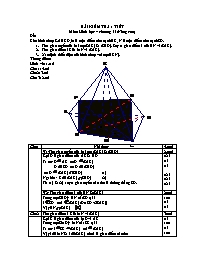
Cho hình chóp S.ABCD, M là một điểm trên cạnh BC, N là một điểm trên cạnh SD.
1. Tìm giao tuyến của hai mp(SAC) & (SBD). Suy ra giao điểm I của BN và (SAC).
2. Tìm giao điểm J Của MN và (SAC).
3. Xác định thiết diện của hình chóp với mp(BCN).
Thang điểm:
Hình vẽ: 1.0 đ
Câu 1: 4.0đ
Câu2: 3.0đ
Câu 3: 2.0đ
Bạn đang xem tài liệu "Bài kiểm tra 1 tiết môn: Hình học – Chương II (nâng cao)", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
BÀI KIỂM TRA 1 TIẾT Môn: Hình học – chương II (Nâng cao) Đề: Cho hình chóp S.ABCD, M là một điểm trên cạnh BC, N là một điểm trên cạnh SD. Tìm giao tuyến của hai mp(SAC) & (SBD). Suy ra giao điểm I của BN và (SAC). Tìm giao điểm J Của MN và (SAC). Xác định thiết diện của hình chóp với mp(BCN). Thang điểm: Hình vẽ: 1.0 đ Câu 1: 4.0đ Câu2: 3.0đ Câu 3: 2.0đ Câu1 Nội dung 4.00đ Ý1:Tìm giao tuyến của hai mp (SAC) & (SBD) 2.00đ Gọi O là giao điểm của AC & BD Ta có: OAC O (SAC) O SD O (SBD) O (SAC)(SBD) (1) Ngaòi ra: S (SAC)(SBD) (2) Từ (1) & (2) suy ra giao tuyến cần tìm là đường thẳng SO. 025 05 05 025 025 025 Ý2: Tìm giao điểm I của BN &(SAC) 200đ Trong mp(SBD): BN cắt SO tại I ISO I (SAC) (Do SO(SAC)) Vậy BN(SAC) = 100 05 05 Câu2 Tìm giao điểm J Của MN và (SAC) 300đ Gọi K là giao điểm của MD và AC Trong mp(SMD): MN cắt SK tại J Ta có: JSK(SAC) J(SAC) Vậy JMN & J(SAC) nên J là giao điểm cần tìm 05 100 05 100 Câu3 Xác định thiết diện của chóp với mp(BCN) 200đ Trong mp(SAC): CI cắt SA tại P Ta có: (BCN)(SAB) = BP (BCN)(SBC) = BC (BCN)(SCD) = CN (BCN)(SAD) = NP Kết luận: Thiết diện là tứ giác BCNP. 05 025 025 025 025 05
Tài liệu đính kèm:
 Hinh-BS3.doc
Hinh-BS3.doc





