Hướng dẫn ôn thi THTPT Môn Toán ban cơ bản

HƯỚNG DẪN ÔN THI TNTHPT NĂM 2009 (Ban cơ bản)
A. ĐẠI SỐ VÀ GIẢI TÍCH
PHẦN 1: HÀM SỐ
Bài toán 1: Khảo sát hàm số
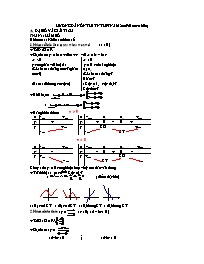
1.Haøm soá baäc 3 : y = ax3 + bx2 + cx + d ( a ¹ 0 ) 
+ TXĐ : D = R
+ Ñaïo haøm: y/ = 3ax2 + 2bx + c vôùi D/ = b2 - 3ac
D/ £ 0 
D/ > 0
y/ cuøng daáu vôùi heä soá a
·KL: haøm soá taêng treân? (giaûm treân?)
 y/ = 0 coù hai nghieäm x1; x2 
·KL: haøm soá taêng? Giaûm?
·Haøm soá khoâng coù cöïc trò 
· Cöïc tri ̣ cöïc ñaïi? Cöïc tieåu?
+ Giôùi haïn: · = 
a > 0
	 · = 
+ Baûng bieán thieân: 
x
- +
x
- x1 x2 +
y/
 +
y/
 + 0 - 0 +
y
 + 
 -
y
 CÑ +
- CT
a < 0
x
- +
x
- x1 x2 +
y/
 -
y/
 - 0 + 0 -
y
+ 
 -
y
+ CÑ 
 CT - 
Chuù yù : duø y/ = 0 coù nghieäm keùp vieäc xeùt daáu vaãn ñuùng
Ñieåm uoán I(-;f(-))
+ Veõ ñoà thò : · xaùc ñinh Cöïc trò ?
	 · ; ñieåm ñaëc bieät
a>0 ; coù 2 CT a0,khoâng CT a<0,khoâng CT
2.Haøm phaân thöùc : y = ( c ¹ 0; ad - bc ¹ 0 ) 
+ TXÑ : D = R\
+ Ñaïo haøm : y/ = 
ad-bc < 0
ad-bc > 0
y/ < 0 " x ÎD
y/ > 0 " x ÎD
Haøm soá khoâng coù cöïc trò
Haøm soá nghòch bieán treân D
Haøm soá ñoàng bieán treân D
+ Tieäm caän: · x =laø tieäm caän ñöùng vì = ¥
 	 · y = laø tieäm caän ngang vì = 
+Baûng bieán thieân :
x
- -d/c +
x
- -d/c +
y/
 - || -
y/
 + || +
y
a/c ||+ 
 - a/c
 y
 +|| a/c
a/c -
+ Veõ ñoà thò : - Veõ tieäm caän , ñieåm ñaëc bieät 
x= -d/ c
y= a/c
x= -d/ c
y= a/c
 	 - Cho 2 ñieåm veà 1 phía cuûa tieäm caän ñöùng veõ moät nhaùnh , laáy ñoái xöùng nhaùnh ñoù qua giao ñieåm hai tieäm caän .
3 Haøm truøng phöông y = ax4 + bx2 + c ( a ¹ 0 ) 
+ TXĐ : D = R
+ Ñaïo haøm: y/ = 4ax3 + 2b.x =2x.(2a x2+ b) 
a,b cuøng daáu
a, b traùi daáu
y/ = 0 Û x = 0 
·KL: tăng? Giảm
 y/ = 0 Û 2x (2ax2 + b) = 0 Û x= 0; x1,2=±
·KL: tăng? Giảm?
·Giaù trò cöïc trò : y(0) = c 
coù moät cöïc trò
· Giaù trò cöïc trò: y(0)= c ; y(±) =-
Coù 3 cöïc trò
a > 0
+ Giôùi haïn : = 
+ Baûng bieán thieân : 
x
- 0 +
x
- x1 0 x2 +
y/
 - 0 +
y/
 - 0 + 0 - 0 +
y
CT
+ +
y
+ CÑ +
 CT CT
a < 0
x
- 0 +
x
- x1 0 x2 +
y/
 + 0 -
y/
 + 0 - 0 + 0 -
y
CĐ
- -
y
 CĐ CĐ
- CT -
 a> 0
 b>0
a< 0
b <0
a0
 a> 0
 b <0
 + Veõ ñoà thò : · cöïc ñaïi , cöïc tieåu ; · y = 0 -> x= ? giaûi pt truøng phöông 
Baøi toaùn 2: Phöông trình tieáp tuyeán :
1. Tieáp tuyeán taïi M(x0; f(x0)) coù phöông trình laø :
 Töø x0 tính f(x0) ; · Ñaïo haøm : y/ = f/(x) => f/(x0) = ? 
P.trình tieáp tuyeán taïi M laø: y = f/(x0)(x- x0) + f(x0)
2. Tieáp tuyeán ñi qua(keû töø) moät ñieåm A(x1; y1) cuûa ñoà thò h/s y =f(x) 
 + Goïi k laø heä soá goùc cuûa ñöôøng thaúng (d) ñi qua A 
 Pt ñöôøng thaúng (d) laø : y = k(x - x1) + y1
 + Ñieàu kieän ñeå ñöôøng thaúng (d) tieáp xuùc vôùi Ñoà thò (C) laø
 heä phöông trình : coù nghieäm 
	Thay (2) vaøo (1) giaûi tìm x => k = ? Keát luaän 
3. Tieáp tuyeán coù heä soá goùc k :
Neáu : tieáp tuyeán // ñöôøng thaúng y = a.x + b => heä soá goùc k = a
 tieáp tuyeán ^ ñöôøng thaúng y = a.x + b => heä soá goùc k = - 
 + giaû söû M(x0; f(x0)) laø tieùp ñieåm => heä soá goùc cuûa tieáp tuyeán f/(x0).
 + Giaûi phöông trình f/(x0) = k => x0 = ? -> f(x0) = ?
 + Phöông trình tieáp tuyeán y = k (x - x0) + f(x0) 
Chuù yù : + Hai ñöôøng thaúng vuoâng goùc nhau : k1.k2 = -1 
 + Hai ñöôøng thaúng song song nhau : k1 = k2 
Baøi toaùn 3: Bieän luaän soá nghieäm cuûa phöông trình baèng ñoà thò :
	+ Giaû söû phaûi bieän luaän soá nghieäm cuûa Pt : F(x; m) = 0 . Trong ñoù ñoà thò haøm soá y = f(x) .
	+ Bieán ñoåi phöông trình veà daïng f(x) = g(m) Ñaët: M = g(m)
	+ y = M laø ñöôøng thaúng naèm ngang ; y =f(x) ñoà thò (C)
	+ Tuyø theo M xeùt söï töông giao cuûa ñoà thò (C) vôùi ñoà thò y = M 
Baøi toaùn 4: xeùt tính ñôn ñieäu
Phöông phaùp xaùc ñònh khoaûng taêng, giaûm haøm soá :	
 + MXĐ D= ?
 + Ñaïo haøm : y/ = ? .. 
 cho y/ = 0 ( neáu coù ) xeùt daáu y/ 
 + BXD (sắp các nghiệm của PT y/ = 0 và giá trị không xác định của hàm số từ trái sang phải tăng dần)
* y/ > 0 thì haøm soá taêng ; y/ < 0 thì haøm soá giaûm 
 + Keát luaän : haøm soá ñoàng bieán , nghòch bieán treân khoaûng ...
Ñònh lyù 2 (duøng ñeå tìm giá trị m): 
	a) f(x) taêng trong khoaûng (a;b) thì f/(x) ³ 0 " x Î (a;b) 
	b) f(x) giaûm trong khoaûng (a;b) thì f/(x) £ 0 " x Î (a;b).
Bài toán 5: Cực trị hàm số 
· Daáu hieäu I :
 + MXĐ D=?
 + Ñaïo haøm : y/ = ? .. 
 cho y/ = 0 ( neáu coù ) xeùt daáu y/ 
 + BBT : (sắp các nghiệm của PT y/ = 0 và giá trị không xác định của hàm số từ trái sang phải tăng dần) 
 + Tính yCÑ ; yCT ; kết luận cực trị ?
Chú ý: 
Nếu hàm số luôn tăng ( giảm)trên (a;b) thì không có cực trị trên (a;b).
Số cực trị của hàm số bằng số nghiệm đơn của phương trình y/ = 0.
đổi dấu qua x0
x0 là cực trị của hàm số ó
· Daáu hieäu II:
 + MXĐ
 + Ñaïo haøm : y/ = ? .. y// = ? .. 
 cho y/ = 0 ( neáu coù ) => x1 , x2 .. .
 + Tính y//(x1); y//(x2).
 Neáu y//(x0) > 0 thì haøm soá ñaït CT taïi x0 , yCT= ? 
 Neáu y//(x0) < 0 thì haøm soá ñaït CÑ taïi x0 , yCÑ= ?
Chuù yù : daáu hieäu II duøng cho nhöõng h/s maø y/ khoù xeùt daáu 
* Nếu y = f(x) là đa thức thì đường thẳng đi qua các điểm cực trị là:
y = phần dư của phép chia f(x) cho f/(x).
Bài toán 6: Giá trị lớn nhất, giá trị nhỏ nhất 
1. Phöông phaùp tìm GTLN vaø GTNN cuûa h/s treân [a;b]:
 + Mieàn ñang xeùt [a;b]
 + Ñaïo haøm : y/ = ? .. 
cho y/ = 0 ( neáu coù ) _ x1 , x2 .. . chỉ chọn các nghiệm thuộc [a;b]
 + Tính y(x1) ; y(x2) . 	So saùnh ® KL 
 y(a) ; y(b) 
 + ? ?
2. P/phaùp tìm GTLN hoaëc GTNN cuûa h/s treân (a;b) hoaëc MXĐ :
 + Mieàn ñang xeùt (a;b) hoaëc TXĐ 
 + Ñaïo haøm : y/ = ? .. 
 cho y/ = 0 ( neáu coù ) xeùt daáu y/ 
 + BBT:
	 * Neáu treân toaøn mieàn ñang xeùt h/s chæ coù 1 CT thì GTNN baèng giaù trò CT 
 * Neáu treân toaøn mieàn ñang xeùt h/s chæ coù 1 CÑ thì GTLN baèng giaù trò CÑ 
 yCÑ
 * Nếu hàm số luôn tăng (giảm) trên (a;b) thì không có cực trị trên khoảng (a;b).
Chuù yù : Khi gaëp h/s khoâng cho mieàn ñang xeùt thì ta tìm TXĐ cuûa h/s ñoù :
 + neáu TXĐ laø moät ñoaïn [a;b]hoaëc nöõa khoaûng thì ta duøng caùch 1 
 + neáu TXĐ laø moät khoaûng thì duøng caùch 2
Bài toán 7 : Giao điểm hai đường cong ( đ.thẳng và một đường cong).
1. Cho hai ñoà thò (C1) : y = f(x) ;	 (C2) : y = g(x) 
Hoaønh ñoä giao ñieåm cuûa (C1) vaø (C2) neáu coù 
laø nghieäm cuûa phöông trình : f(x) = g(x) (1) 
· pt(1) voâ nghieäm (C1) vaø (C2) khoâng coù ñieåm chung 
· pt(1) coù n nghieäm (C1) vaø (C2) coù n ñieåm chung 
* Số nghiệm của (1) là số giao điểm của hai đường cong.
 2. Ñieàu kieän tieáp xuùc : 
Ñoà thò (C1) tieáp xuùc (C2) heä pt coù nghieäm
Bài toán 8: Caùch xaùc ñònh tieäm caän :
*Tieäm caän ñöùng : => x = x0 laø tieäm caän ñöùng 
 Chuù yù : tìm x0 laø nhöõng ñieåm haøm soá khoâng xaùc ñònh 
*Tieäm caän ngang : => y = y0 laø tieäm caän ngang
 Chuù yù : haøm soá coù daïng phaân thöùc ( hoaëc coù theå ñöa veà daïng phaân thöùc ) vaø baäc töû £ baäc maãu thì coù tieäm caän ngang 
Phần 2: Hàm số mũ và logarit
Bài toán 1: Dùng công thức tính các biểu thức có chứa hàm số mũ hoặc hàm số logarit
 a-n = ; a0 = 1 0 ; ( m; n nguyeân döông , n > 1)
· Caùc quy taéc: 
ax.ay = ax+y 	(a.b)x =ax.bx
· Haøm soá muõ : y = vôùi a > 0 ; a ¹ 1 
TXĐ : D = R 	MGT : (0; +¥ )
+ a > 1 ; h/s ñoàng bieán : x1 > x2 Û > 
+ 0 x2 Û < 
* Hàm số logarit: 
a = logaN Û aa = N logax = b Û x= ab
· Ñaëc bieät : = x ; log = x ; loga1 = 0
· Caùc qui taéc bieán ñoåi : vôùi a , B , C > 0 ; a ¹ 1 ta coù:
	log(B.C) = logB + logC
log = logB - logC	log = logB
· Coâng thöùc ñoåi cô soá : vôùi a , b , c > 0 ; a , c ¹ 1 ta coù :
loga.logb = b Û 
0 < a, b ¹ 1 : logb = 
Chuù yù : log10x = lg x ; logx = ln x 
· Haøm soá Logarit: y = logx vôùi a > 0 ; a ¹ 1 
TXĐ : D = (0 ; +¥ )	MGT : R 
+ a > 1 ; h/s ñoàng bieán : x1 > x2 > 0 Û logx1 > logx2 
+ 0 x2 > 0 Û logx1 <logx2 
Bài toán 2: Tính đạo hàm của các hàm số mũ và logrit
(ex) / = ex 	-> ( eu)/ = u/.eu
( ax) / = ax.lna 	-> ( au)/ = u/.au.lna
(lnx) / = x Î(0;+¥)	-> (ln½u½)/ = 
(logax) / = 	-> (logau )/ = 
Bài toán3: giải phương trình mũ và logarit :
· Daïng cô baûn:
= Û f(x) = g(x) 
= 1 Û ( u -1 ).v(x) = 0 ( trong ñoù u coù chöùa bieán )
= b ( vôùi b > 0 ) Û f(x) = logb
hoặc
logf(x) = logg(x) Û
daïng: Û f(x) = 
 = b Û 
· Ñaët aån phuï : 
a. +b. + g = 0 ; Ñaët : t = Ñk t > 0
 a.+b.+ g = 0 ; Ñaët : t = Ñk t > 0
a.+b.+ g = 0 vaø a.b = 1; Ñaët: t = ;=
a.+b.+ g. = 0 ; Ñaët t = 
· Logarit hoaù hai veá :
Bài toán 4: Giải bất phương trình mũ và logarit
· Daïng cô baûn :
10 > Û 
20 > b Û Neáu b £ 0 coù nghieäm "x
	 Neáu b > 0 f(x) > logb neáu a > 1
	 f(x) < logb neáu 0 < a < 1 
 30 < b Û Neáu b £ 0 thì pt voâ nghieäm
	 Neáu b > 0 ; f(x) 1
	 f(x) > logb neáu 0 < a < 1 
·logf(x) > logg(x) Û Ñk: f(x) > 0 ; g(x) > 0 ; 0 < a ¹ 1
 (a-1)[ f(x) - g(x) ] > 0 
·logf(x) > b 	Û * Neáu a > 1 : bpt laø f(x) > 
	 * Neáu 0 < a < 1 bpt laø 0 < f(x) < 
·logf(x) 1 : bpt laø 0 < f(x) < 	 
 * Neáu 0 
·> 1 Û u(x) > 0 vaø [ u(x) -1 ].v(x) > 0 
· 0 vaø [ u(x) -1 ].v(x) < 0 
Lưu ý: 
 *) trong trường hợp có ẩn dưới cơ số thì chúng ta nên sử dụng công thức sau để bài toán trở nên dễ dang hơn.
10 > ó (a-1)(f(x) - g(x)) > 0.
20 logf(x) > logg(x) ó (a-1)(f(x) - g(x)) > 0.
 *) Khi giải bài toán bất phương trình mũ hoặc logarit thì phải nắm thật vững tính chất đơn điệu của hai hàm số trên.
 *) Nắm vững phép lấy hợp, lấy giao của hai hay nhiều tập hợp số.
Phần 3: Nguyên hàm.
Bài toán 1: Tìm nguyên hàm cơ bản (dựa vào bảng nguyên hàm của các hàm số cơ bản).
+ C (a ¹-1 )
 = ln½x½ + C ( x¹ 0)
= ex + C
= + C 
(a ¹-1)
 = ln½ax+ b½ + C 
eax+b + C 
=
 = Sinx + C 
 = - Cos x + C 
 == tgx
 = 
 = -Cotgx
= Sin(ax+ b) + C 
= -Cos(ax+ b) + C
=tg(ax+ b) + C
= -Cotg(ax+ b) + C
Bài toán 2: Tìm nguyên hàm bằng phương pháp đổi biến số.
Dạng 1: Tính I = bằng cách đặt t = u(x)
Đặt t = u(x)
I = 
 Dạng 2: Tính I = Nếu không tính được theo dạng 1 nhưng trong tích phân có chứa một trong số các hàm biểu thức sau thì có thể đổi biến như sau:
 thì đặt x = asint ;;; thì đặt x = atant.
Bài toán 3: Tìm nguyên hàm bằng phương pháp từng phần:
Nếu u(x) , v(x) là hai hàm số có đạo hàm liên tục trên I
Hay ( với du = u’(x)dx, dv = v’(x)dx)
 phân tích các hàm số dễ phát hiện u và dv
 @ Dạng 1 với f(x) là đa thức:
 Đặt 
 Sau đó thay vào công thức để tính
 @ Dạng 2: 
 Đặt 
 Sau đó thay vào công thức để tính
@ Dạng 3: 
Ta thực hiện từng phần hai lần với u = eax
Bài toán 4: Tìm nguyên hàm của các hàm số lượng giác (một số dạng cơ bản).
 Dạng 1: ;
 .
 * Thực hiện công thức biến đổi tích thành tổng rồi tính tích phân.
 Dạng 2: (n,m là các số nguyên dương)
 *) Nếu n lẻ, m chẵn thì đặt t = cosax.
 *) nếu m lẻ, n chẵn thì đặt t = sinax.
 *) Nếu n,m đều chẵn thì : Dùng công thức nhân đôi sau đó dung tiếp công thức hạ bậc để tính. (nếu một trong 2 số n hoặc n = 0 số còn lại là số chẵn thì ta chỉ dung công thức hạ bậc).
  ... 
 Nếu f(x) = 0 vô nghiệm trên (a;b) hoặc có có nghiệm nhưng không có nghiệm nào thuộc [a;b] hoặc có một nghiệm x = a hoặc x = b các nghiệm còn lại không thuộc [a;b] thì 
 = 
 Nếu f(x) = 0 có nghiệm x = c Î(a;b) thì = 
*Chú ý 
 1) Nếu có nhiều hơn 1 nghiệm trên (a;b) thì vẫn dung công thức trên tùy theo trường hợp nghiệm như thế nào. (cách làm này có lợi vì ta khôngcần xét dấu f(x)).
 2) Ở mức độ thi TNTHPT không cần nắm bất đẳng thức tích phân.
Phần 5: Diện tích hình phẳng - thể tích vật thể tròn xoay.
Bài toán 1: Tính diện tích hình phẳng 
a
b
x
y
· Hình phaúng giôùi haïn bôûi :
Dieän tích : S = 
Chuù yù : neáu thieáu caän a, b giaûi pt : f(x) = 0
a
b
x
y
y=f(x)
y=g(x)
· Hình phaúng giôùi haïn bôûi :
Dieän tích : S = 
Chuù yù : 1) Neáu thieáu caän a, b giaûi pt : f(x) = g(x) 
 2) Nếu bài toán qua phức tạp thì ta có thể vẽ hình để xác định hình phẳng hoặc tính thong qua tổng hoặc hiệu của nhiều hình.
Bài toán 2:Tính thể tích vật thể tròn xoay : 
 * Theå tích hình troøn xoay do hình phaúng giôùi haïn bôûi caùc ñöôøng :
x
b
quay quanh truïc Ox vaø f(x) ³ 0 treân [a;b] thì V = 
* Theå tích hình troøn xoay do hình phaúng giôùi haïn bôûi caùc ñöôøng :
x
b
quay quanh truïc Oy vaø f(y) ³ 0 treân [a;b] thì V = 
Phần 6: Số phức
 Bài toán 1: Tìm số phức, tính môđun,
Cho hai số phức a+bi và c+di.
1) a+bi = c+di ó a = c; b = d. 2) môđun số phức
3) số phức liên hiệp z = a+bi là = a - bi.
* z+ = 2a; z.= 
4) (a+bi ) +( c+di) = (a+c)+(b+d)i 
5) (a+bi ) -( c+di) = (a-c)+(b-d)i.
6) ) (a+bi )( c+di) = (ac - bd)+(ad+bc)i 
7) z = 
Bài toán 2: Giải phương trình bậc 2.
Cho phương trình ax2 + bx + c = 0. với D = b2 - 4ac.
Nếu D = 0 thì phương trình có nghiệp kép (nghiệm thực)
Nếu D > 0 thì phương trình có hai nghiệm thực: 
Nếu D < 0 thì phương trình có hai nghiệm phức 
B. HÌNH HỌC.
Phần 1: Thể tích, diện tích của các khối hình
Bài toán 1: Tính diện tích xung quanh (Sxq), diện tích toàn phần(Stp) của khối nón,trụ,cầu.
Khối nón: Sxq = prl; Stp = pr(r + l).
Khối trụ: Sxq = 2prl; Stp = 2pr(r + l).
Khối cầu: S = 4pr2 .
Bài toán 2: Tính thể tích các khối hình.
 * Khối hình chóp V = ; * Khối nón V = 
 * Khối hình trụ V = pr2h ; * Khối cầu V = 
 * Khối lăng trụ: V= Bh.
Phần 2: Phương pháp tọa độ trong không gian
 = (x;y;z) Û = x.+ y. + z. 
Tính chaát : 	Cho = (a1;a2; a3) , = (b1;b2; b3)
· ±=(a1 ± b1; a2 ± b2; a3 ± b3)
· k. = (ka1;ka2;ka3) 	k Î R 
Tích voâ höôùng : = a1.b1 + a2.b2 +a3.b3=½½.½½Cos j
 Cos j = 
 Û a1.b1 + a2.b2 + a3.b3 = 0 
cuøng phöông ;¹ Û = k.Û [,] = 
Toaï ñoä ñieåm:
M = (x;y;z)Û = x.+ y. + z. 
= ( xB- xA ; yB-yA;zB -zA)
· M chia ñoaïn AB theo tæ soá k¹1 ( = k)
 	Thì M: 
· I laø trung ñieåm cuûa AB thì I:
· G laø troïng taâm tam giaùc ABC thì G:
· Tích coù höôùng cuûa 2 veùc tô : 
 [,] = 
 * [,] ^ ; [,] ^ 
 · Ñk ñoàng phaúng cuûa 3 veùc tô :
 	,, ñoàng phaúng Û [,].= 0
· ÑK ñeå 4 ñieåm A,B,C,D khoâng ñoàng phaúng ( taïo thaønh töù dieän ) laø: ba veùc tô ,, khoâng ñoàng phaúng [,].¹ 0 
· Dieän tích tam giaùc ABC : SABC = 
 	 Hoặc SABC = .½[,]½ 
· Theå tích töù dieän ABCD : VABCD = ½[,].½
· Theå tích hình hoäp : VABCD.A'B'C 'D' = ½[,].½ 
Bài toán 1:Xaùc ñònh ñieåm , tọa độ vectơ trong khoâng gian , c/m tính chaát hình hoïc ...
Bài toán 2: Tích voâ höôùng , tích coù höôùng , goùc giöõa hai veùc tô :
Bài toán 3:Veùc tô ñoàng phaúng , khoâng ñoàng phaúng,theå tích hình hoäp, töù dieän:
Phần 3: Mặt cầu.
Bài toán 1: xác định tâm và bán kính mặt cầu
Phöông trình maët caàu taâm I(a;b;c) ; bk R laø :
 (x -a)2 + (y - b)2+ (z-c )2 = R2
 Phöông trình toång quaùt cuûa maët caàu ( S):
 x2 + y2+ z2+ 2.Ax+ 2.By + 2.Cz + D = 0 vôùi A2 + B2 + C2-D > 0 
 coù taâm I(-A ;-B;-C) ; baùn kính R = 
Bài toán 2: Viết phương trình mặt cầu
· Pt.maët caàu (S) taâm I(a;b;c) vaø ñi qua M1(x1;y1;z1) 
+ Baùn kính R = IM1 = 
· Pt.maët caàu (S) ñöôøng kính AB :
 + Taâm I laø trung ñieåm AB => I(;;)
 + Baùn kính R = IA
· Pt. maët caàu (S) qua boán ñieåm A,B,C,D:
p/ phaùp : Pt toång quaùt maët caàu (S)
x2 + y2+ z2+ 2.Ax+ 2.By + 2Cz + D = 0 (1)
Thay laàn löôït toaï ñoä 4 ñieåm vaøo (1) => giaûi heä tìm heä soá A;B;C;D 
· Pt.maët caàu (S) taâm I(a;b;c) vaø tieáp xuùc maët phaúng (a)
	baùn kính R = d(I; (a))
Bài toán 3: xác định vị trí tương đối giữa mặt cầu và mặt phẳng
(a) : A x + B y + Cz +D = 0 ; (S): (x -a)2 + (y-b)2 +(z-c)2 = R2 
Tính d(I; (a)) = ?
Neáu:· d(I; a ) > R a vaø S khoâng coù ñieåm chung ( rôøi nhau)
 · d(I; a ) = R a tieáp xuùc vôùi S ( a laø mp tieáp dieän) 
(a) Ç (S) ={M0} ; 
Cách viết mặt phẳng tiếp diện : (a) qua M0 nhaän laøm VTPT
 · d(I; a ) a caét maët caàu (S) theo moät ñöôøng troøn (C) 
taâm H; baùn kính r 
	* P.t ñ.troøn (C ) A x + B y + Cz +D = 0
 	 (x -a)2 + (y-b)2 + (z-c)2= R2 
+ Taâm H laø hình chieáu cuûa I leân mp a
+ baùn kính r = 
Caùch xaùc ñònh H: + Laäp pt ñ. thaúng (d) qua I nhaän laømVTCP
(d) thay vaøo pt mp(a) => giaûi t => toaï ñoä ñieåm H 
Bài toán 4: Cách viết mặt phẳng tiếp diện tại điểm M0: 
 +) Xác định tâm và bán kính của mặt cầu (S)
+) Tính 
+) Mặt phẳng tiếp diện (a) qua M0 nhaän laøm VTPT.
Bài toán 5: Xác định tâm H và bán kính r đường tròn giao tuyến của mặt cầu (S)và mặt phẳng(a).
+ baùn kính r = 
Caùch xaùc ñònh H: 
+ Laäp pt ñ. thaúng (d) qua I nhaän laømVTCP
(d) thay vaøo pt mp(a) => giaûi tìm t = ? => toaï ñoä ñieåm H 
Phần 4: Mặt phẳng, đường thẳng.
Bài toán 1: các viết phương trình mặt phẳng:
* (ABC): +) tính 
 +) VTPT của (ABC) là 
=> viết mặt phẳng đi qua A có VTPT .
* (a,b) : nếu a//b thì VTPT với AÎ a; B Î b.
 Nếu a cắt b thì 
*(A;a) thì VTPT với BÎ a.
* (a) //(b) thì VTPT 
* (a) ^a thì VTPT 
* (a) có hai vectơ chỉ phương thì .
*(a) đi qua 2 điểm A và B đồng thời chứa đ.thẳng a hoặc // a hoặc có VTCP thì ( thay =)
*(a) vuông góc cả hai mặt phẳng (P) và (Q). thì VTPT 
* Mặt phẳng trung trực của đoạn thẳng AB.
 +) Xác định trung điểm M của đoạn thẳng AB.
 +) Tính vectơ .
Mặt phẳng trung trực đi qua M có VTPT .
* (a) song song đường thẳng và vuông góc với một mặt phẳng thì 
.
* (a) chứa đ.thẳng (D) và ^(b) .
 +) chọn M trên đ.thẳng (D).
 +) VTPT của (a) là 
* Viết PT mặt phẳng (P) chứa đường thẳng (d) và song song với (d/).
 +) chọn M trên đ.thẳng (d).
 +) VTPT của (a) là 
 => Viết PT mp(P) đi qua M và có VTPT 
Bài toán 2 viết phương trình đường thẳng.
*D đi qua điểm A và có VTCP 
* D đi qua 2 điểm A và B => D đi qua A có VTCP .
*D đi qua A và // (D) => D qua A có VTCP .
*D đi qua A và ^(a) thì D qua A có VTCP là .
* D là giao tuyến của hai mặt phẳng (a) và (b) thì 
 +) VCTP của D là .
 +) Cho một ẩn bằng 0 giải hệ 2 ẩn còn lại tìm điểm M?
=> D đi qua M có VTCP là 
* D là hình chiếu của đ.thẳng (D) lên mp (b)
 *) Viết phương trình mp(P) chứa (D) và vuông góc mp(b)
 +) chọn M trên đ.thẳng (D).
 +) VTPT của (a) là 
 * ) VTCP của D là 
 * ) cho một ẩn x = 0 giải hệ gồm 2 ẩn y và z của 2 PT hai mặt phẳng (P) và (b)=> M? => D đi qua M có VTCP 
* Cách viết phương trình đường cao AH của DABC.
 +) Tìm tọa độ VTPT của mp(ABC) là = ?.
 +) Tìm tọa độ VTCP của đường cao AH là: = ?
 => Viết PT đường cao AH đi qua A có VTCP .
* Cách viết phương trình đường trung trực của cạnh BC của DABC.
 +) Tìm tọa độ VTPT của mp(ABC) là = ?.
 +) Tìm tọa độ VTCP của trung trực là: = ?.
 +) Tìm tọa độ điểm M là trung điểm đoạn thẳng BC.
=> Đường trung trực cạnh BC của DABC là đường thẳng đi qua M có VTCP .
Bài toán 3: tìm hình chiếu của một điểm lên một mặt phẳng hoặc đ.thẳng. 
* Tìm hình chiếu H của M lên (a)
 +) Viết PT đ.thẳng (D) qua M có VTCP là .
 +) giải hệ gồm 
 +) Hình chiếu H là giao điểm của (a) và (D) là nghiệm của hệ trên.
* Tìm hình chiếu H của M lên đường thẳng (D).
 +) Viết PT mặt phẳng (P) qua M có VTPT là .
 +) giải hệ gồm 
 +) Hình chiếu H là giao điểm của (a) và (D) là nghiệm của hệ trên.
Bài toán 4: Tìm tọa độ điểm A/ đối xứng với điểm A qua đt hoặc mp
 * Đối xứng qua mp(a)
 +) Viết PT đ.thẳng (D) qua M có VTCP là .
 +) giải hệ gồm 
 +) Hình chiếu H là giao điểm của (a) và (D) là nghiệm của hệ trên.
 +) Tọa độ điểm đối xứng A/ : 
* Đối xứng quađường thẳng (D).
 +) Viết PT mặt phẳng (P) qua M có VTPT là .
 +) giải hệ gồm 
 +) Hình chiếu H là giao điểm của (a) và (D) là nghiệm của hệ trên.
 +) Tọa độ điểm đối xứng A/ : 
Bài toán 4: xác định vị trí tương đối giữa mp và mp, đt và đt, đt và mp.
* Vị trí tương đối giữa mp (P) và mp(Q).
(P) : Ax + By + Cz + D = 0 ; (Q) : A/x + B/y + C/z + D/ = 0 
vôùi =(A;B;C) vaø =(A/; B/ ; C/ )
(P) º (Q) === 
(P) // (Q) == ¹ 
(P) cắt (Q) ¹Ú ¹ Ú ¹
Chuù yù :· a ^ a/ .= 0 AA/ + BB/ + CC/ = 0 
	· a caét a/ vaø khoâng cuøng phöông 
* vị trí tương đối giữa đ.thẳng (d1) và (d2).
 Xác định các VTCP =(a;b;c) , =(a/;b/; c/ ) ;Tính [,] 
Neáu :[,]= 
 +) chọn M1 Î(d1). Nếu M1Ï d2 thì d1 // d2 
 Nếu M1 Î(d2) thì d1 º d2 
 Neáu [,] ¹ . Ta giải hệ theo t và t/ (cho PTTS của hai đ.thẳng = theo tùng thành phần ).
 +) hệ có nghiệm duy nhất t và t/ thì d1 caét d2 => giao điểm.
 +) nếu hệ VN thì d1 cheùo d2
* Vị trí tương đối giữa đ.thẳng (D) và mặt phẳng (P).
 +) thay PTTS của đ.thẳng (D) vào PT mp(P) ta được PT theo ẩn t.
 +) nếu PTVN thì (D)//mp(P).
 Nếu PTVSN thì (D) Ì mp(P).
 Nếu PT có nghiệm duy nhất thì (D) cắt mp(P) =>giao điểm?
Hoặc có thể dung cách sau:
 +) tìm tọa độ VTCP của (D) và VTPT của mp(P).
 +) Tính tích vô hướng . = ? 
 Nếu tích vô hướng này . 0 thì (D) cắt mp(P).
 Nếu . = 0 thì chọn điểm M bất kỳ trên (D) sau đó thay vào PT mặt phẳng (P) nếu thỏa mãn thì (D) Ì mp(P). còn ngược lại thì (D)//mp(P).
Bài toán 5: Tính khoảng cách.
* từ điểm A(x0;y0;z0) đến mặt phẳng (P): Ax+By+Cz+D = 0 .
 d(A;(a)) = 
* (P)//(Q) thì d((P),(Q)) = d(A;(Q)) với mọi điểm A chọn tùy ý trên (P)
* Khoảng cách tử đường thẳng (d) đến mặt phẳng (P) với (d)//mp(P)
 +) chọn điểm M bất kỳ trên (d). tính d(M;(d)) = ?
 +) d((d), mp(p)) = d(M,(mp(P))
* Khoảng cách từ điểm A đến đường thẳng (D)(không có công thức tính trong chương trình mới phân ban đối với ban cơ bản) nhưng ta có thể tính như sau:
 +) lập PT mp(Q) qua A và vuông góc với (D).
 +) Tìm giao điểm H của mp(P) và đ.thẳng (D).
 +) Khoảng cách cần tìm là đoạn thẳng AH.
* Khoảng cách giữa hai đường thẳng song song (d) và (d/).
 +) Chọn điểm M bất kỳ trên (d).
 +) Viết PT mặt phẳng (P) qua M có VTPT là .
 +) Tìm điểm N là giao điểm của (d/ ) và mp(P) ( bằng cách giải hệ gồm PTcủa (d/) và PT mặt phẳng (P) => nghiệm x,y,z là tọa độ điểm N).
 +) Khoảng cách cần tìm là độ dài đoạn thẳng MN.
* Khoảng cách giữa hai đường thẳng chéo nhau (d) và (d/).
 * Viết PT mặt phẳng (P) chứa đường thẳng (d) và song song với (d/).
 +) chọn M trên đ.thẳng (d).
 +) VTPT của (a) là 
 => Viết PT mp(P) đi qua M và có VTPT 
 * Chọn điểm N bất kỳ trên (d/) . Tính d(N, mp(P)) =?
 => d((d), (d/)) = d(N, mp(P)) 
 Bài toán 6: Tính góc .
* Góc giữa hai mp (P) A1x+B1y+C1z+D1 = 0 
 và mp(Q) A2x+B2y+C2z+D2 = 0 
thì = 
 Với 
* Góc giữa đường thẳng (D): 
 và mặt phẳng Ax+By+Cz+D = 0 là 
 SinY = = 
 Với 
Góc giữa hai đường thẳng (D1) : Và (D2): 
 thì =