Giáo án môn Giải tích 12 tiết 33: Khảo sát hàm số. Bài tập
Tiết 33 :
. Ổn định lớp :
Ổn định trật tự, kiểm diện sĩ số.
. Kiểm tra :
. Nội dung bài mới:
3. Khảo sát hàm số y = ax3 + bx2 + cx + d
1. Các ví dụ cụ thể
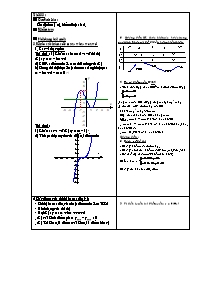
Thí dụ 1 : 1) Khảo sát hàm số và vẽ đồ thị
(C) : y = x3 – 3x + 2
2) CMR : điểm uốn là tâm đối xứng của (C)
3) Dùng đồ thị biẹn luận theo m số nghiệm pt :
x3 – 3x + 2 – m = 0 (*)
Bạn đang xem tài liệu "Giáo án môn Giải tích 12 tiết 33: Khảo sát hàm số. Bài tập", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
y x y’ y” -¥ +¥ + -1 0 1 0 - 0 + - 0 + -¥ +¥ 4 CĐ 2U 4 CT Tiết 33 : . Ổn định lớp : Ổn định trật tự, kiểm diện sĩ số. . Kiểm tra : . Nội dung bài mới: 3. Khảo sát hàm số y = ax3 + bx2 + cx + d 1. Các ví dụ cụ thể Thí dụ 1 : 1) Khảo sát hàm số và vẽ đồ thị (C) : y = x3 – 3x + 2 2) CMR : điểm uốn là tâm đối xứng của (C) 3) Dùng đồ thị biẹn luận theo m số nghiệm pt : x3 – 3x + 2 – m = 0 (*) Thí dụ 2 : 1) Khảo sát và vẽ (C) : y = (x – 1)3 2) Viết pt tiếp tuyến của (C) tại điểm uốn 1) Hướng dẫn HS thực hiện các bước trong quá trình khảo sát để đi đến bảng biến thiên. 2) Ta có điểm uốn O’(0;2) - Tịnh tiến Oxy theo ta được hệ trục O’xy . Suy ra pt của (C) / O’xy là y = g(x) = x3 – 3x . y là s lẻ Þ O’ là tâm đx của (C) 3) (*) « x3 – 3x + 2 = m Đây là pt hđgđ của (C) và đt y = m KQ: . m 4 (*) có 1 nghiệm 0 . m = 0 V m = 4 (*) có 1 nghiệm đơn, đơn, 1nghiệm kép . m Ỵ (0,4) (*) có 3 nghiệm pb Hướng dẫn : 1) Cách vẽ đồ thị: - Chú ý điểm uốn là tâm đx. - Chú ý vị trí các điểm vô tận (-¥,-¥),(+¥,+¥) - Có thể lấy thêm một điểm đặc biệt. Chẳng hạn : Chú ý các khoảng lồi, lõm 2. Đặc điểm của đồ thị hàm số bậc 3 - Đồ thị hàm số bạc 3 nhận điểm uốn làm TĐX - Hình dạng của đồ thị - Gọi (C) : y = ax3 + bx2 + cx + d . (C) cắt Ox 3 điểm pb Û ymax – ymin < 0 . (C) TX Ox tại 1 điểm (cắt Ox tại 1 điểm khác) . (C) cắt Ox tại 1 điểm a > 0 a < 0 a > 0 a < 0 y x y x y x y x . Củng cố : - Chú ý các đặc điểm cơ bản và hình dạng của đồ thị hàm số bậc 3. - Khi lập bảng biến thiên, trường hợp đồ thị có CĐ, CT cần thử lại xem điểm uốn có phải là trung điểm của đoạn thẳng nối CĐ, CT không ? - Khi vẽ đồ thị chú ý điểm uốn là tâm đối xứng. và (D), từ đó suy ra số nghiệm của pt. . Dặn dò : 2) Pt tiếp tuyến tại điểm uốn : y = 0 (Ox) Phương pháp chứng minh O’(x0, y0) là tâm đối xứng của đồ thị hàm số y = f(x) . Tịnh biến Oxy theo . Tìm pt (C) / O’xy . Giả sử (C) : y g(x) / O’xy . Ta chứng minh y là hàm số lẻ Phương pháp dùng đồ thị biện luận số nghiệm của phương trình . Biến đổi pt về dạng f’(x) = g(m) = K . Đây là phương trình bđgđ của (C):y = f(x) và (D) : y =K . Căn cứ vào đồ thị ta biết được số giao điểm (C) D. RÚT KINH NGHIỆM:
Tài liệu đính kèm:
 C2-33.doc
C2-33.doc





