Đề kiểm tra 1 tiết môn: Hình học lớp 11 tiết: 42(theo PPCT - Ban nâng cao)

ĐỀ KIỂM TRA 1 TIẾT
MÔN: HÌNH HỌC
LỚP: 11
TIẾT: 42( Theo PPCT- Ban Nâng Cao)
NHÓM SOẠN THẢO: NHÓM 1 ( LỚP 2)
I.Ma trận mục tiêu giáo dục và mức độ nhận thức.
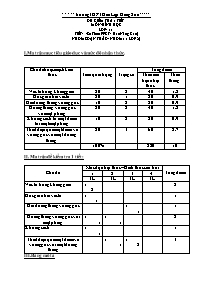
Chủ đề hoặc mạch kiến thức
Tầm quan trọng
Trọng số
Tổng điểm
Theo ma trận nhận thức
Theo thang
Véc tơ trong không gian
20
2
40
1.8
Góc giữa hai véc tơ
20
1
20
0.9
Hai đường thẳng vuông góc
10
2
20
0.9
Đường thẳng vuông góc với mặt phẳng
20
2
40
1.8
Khoảng cách từ một điểm tới một mặt phẳng
10
2
20
0.9
Thiết diện qua một điểm và vuông góc với một đường thẳng
20
3
60
2.7
100%
220
10
II. Ma trận đề kiểm tra 1 tiết:
Chủ đề
Mức độ nhận thức – Hình thức câu hỏi
Tổng điểm
1
2
3
4
TL
TL
TL
TL
Véc tơ trong không gian
1
 2 
2
Góc giữa hai véc tơ
1
 1
1
 Hai đường thẳng vuông góc
1
1
1
Đường thẳng vuông góc với mặt phẳng
1
1
1
1
2
Khoảng cách
1
1
1
Thiết diện qua một điểm và vuông góc với một đường thẳng
1
1
1
2
3
III. Bảng mô tả
Câu 1a : Chứng minh đẳng thức véc tơ.
Câu 1b: Tính góc giữa hai véc tơ.
Câu 2a: Chứng minh đường thẳng vuông góc với mặt phẳng .
Câu 2b: Chứng minh đường thẳng vuông góc với mặt phẳng.
Câu 3a: Tính khoảng cách từ một điểm tới một mặt phẳng.
Câu 3b: Xác định thiết diện của hình chóp
Câu 3c: Tính diện tích thiết diện
IV. Đề thi:
Câu 1: (3 điểm) Cho tứ diện ABCD với và AB = a; đáy BCD là tam giác đều cạnh 2a.
a) Chứng minh: 
b) Gọi H là trung điểm của cạnh CD. Tìm góc tạo bởi và 
Câu 2: (4 điểm) Cho hình chóp S.ABCD có SA (ABCD), đáy ABCD là hình vuông. Gọi M, N lần lượt là trung điểm của cạnh SB và SD. Chứng minh
a) 
b) MN (SAC) 
c) Trên AB và BC lần lượt lấy điểm I và K so cho . Chứng minh IKMN
Câu 3: (3 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, các cạnh bên đều bằng 
a) Tính khoảng cách từ S tới mặt phẳng (ABCD)
b) Gọi (P) là mặt phẳng qua A và vuông góc với SC. Hãy xác định thiết diện của chóp với mặt phẳng (P).
c) Tính diện tích của thiết diện nói trên.
V. Đáp án – Thang điểm
Câu
Nội dung bài làm
Điểm
1 
Vẽ hình:
a) Chứng minh: 
Biến đổi vế trái: 
0,5 điểm
0,5 điểm
0,5 điểm
 0,5 điểm
b) Góc tạo bởi và 
Tính BH = a
(; ) = 1800 – 300 = 1500
0,5 điểm
0,25 điểm
0,25 điểm
 3
S
A1
A
B
B1
O1
D1
D
C
O
S
B
C
D
A
M
N
I
K
a) Chứng minh 
b) Chứng minh MN (SAC)
(1)
MN // BD (2) 
Từ (1) và (2) MN (SAC)	
c) Chứng minh IKMN
Từ (3) 
MNAC {do MN (SAC)} (4) 
Từ (3) và (4) MN IK
Vẽ hình: 
a) Gọi O là tâm của hình vuông ABCD.
Theo bài ra ta có: 
Vậy SO là khoảng cách từ S tới mặt phẳng (ABCD).
Do nên tam giác SOB vuông tại O.
Ta có : 
b) Ta có : 
Trong mặt phẳng (SAC) ta dựng . Giả sử cắt SO tại 
Trong mặt phẳng (SBD) qua kẻ . Suy ra . Vậy và mặt phẳng (P) chính là mặt phẳng . Thiết diện cần tìm là tứ giác 
c) Ta có: ( Theo chứng minh trên)
Do nên .
Mặt khác: 
+ Hai tam giác vuông SOC và đồng dạng ( chung)
nên: 
*
*
+ Hai tam giác vuông SOC và đồng dạng ( chung)
nên: 
*
*
Vậy diện tích của thiết diện cần tìm là: 
1,0 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
 0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5 điểm
0,5điểm
0,5 điểm
0,5 điểm
*Chú ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa