Đề kiểm tra 1 tiết Giải tích 12 nâng cao

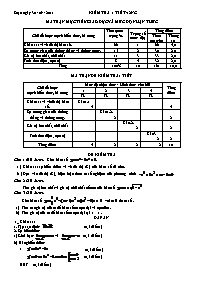
Soạn ngày 30 / 09 / 2011 KIỂM TRA 1 TIẾT-12NC
MA TRẬN MỤC TIÊU GIÁO DỤC VÀ MỨC ĐỘ NHẬN THỨC
Chủ đề hoặc mạch kiến thức, kĩ năng
Tầm quan 
trọng %
Trọng số
(mức độ)
Tổng điểm
Theo
ma trận
Thang
10
Khảo sát và vẽ đồ thị hàm số.
66
1
66
4,0
Sự tương giao của đường thẳng và đường cong.
15
2
30
2,0
Giá trị lớn nhất, nhỏ nhất
11
3
33
2,0
Tính đơn điệu , cực trị
8
4
32
2,0
Tổng
100%
10
161
10,0
MA TRẬN ĐỀ KIỂM TRA 1 TIẾT
Chủ đề hoặc
mạch kiến thức, kĩ năng
Mức độ nhận thức - Hình thức câu hỏi
Tổng điểm
1
2
3
4
TL
TL
TL
TL
Khảo sát và vẽ đồ thị hàm số.
Câu 1.1
 4
4
Sự tương giao của đường thẳng và đường cong.
Câu 1.2.
 2
2
Giá trị lớn nhất, nhỏ nhất
Câu .2.
2
2
Tính đơn điệu , cực trị
Câu 3
 2
2
Tổng điểm
4
2
2
2
10
ĐỀ KIỂM TRA
Câu 1 (6,0 điểm). Cho hàm số .
 a ) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
 b ) Dựa vào đồ thị (C), biện luận theo m số nghiệm của phương trình .
Câu 2 (2,0 điểm). 
 Tìm giá trị lớn nhất và giá trị nhỏ nhất nếu có của hàm số 
Câu 3 (2,0 điểm). 
 Cho hàm số với m là tham số .
Tìm các giá trị của m để hàm số có cực đại và cực tiều .
Tìm giá trị của m để hàm số có cực đại tại x = 1 .
ĐÁP ÁN
 a_ Khảo sát
1. Tập xác định: (0,5 đi ểm )
2. Sự biến thiên:
a) Giới hạn: và (0,5 đi ểm )
b) Bảng biến thiên:
 (0,5 đi ểm )
 (0,5 đi ểm )
BBT (0,5 đi ểm )
x
- 0 2 +
y’
 + 0 - 0 +
y
 3 +
- -1 
+ Hàm số nghịch biến trên mỗi khoảng và , đồng biến trên khoảng . (0,5 đi ểm )
+ Hàm số đạt cực đại tại điểm ; giá trị cực đại của hàm số là . 
+ Hàm số đạt cực tiểu tại điểm ; giá trị cực tiểu của hàm số là . (0,5 đi ểm )
3. Đồ thị:
 + Giao điểm của đồ thị với trục tung là điểm .
 + Giao điểm của đồ thị với trục hoành là các điểm .
 + Đồ thị đi qua điểm .
 (0,5 đi ểm )
 b-Dựa vào đồ thị (C), biện luận theo m số nghiệm của phương trình: 
 (1)
Ta có : . (0,5 đi ểm )
Số nghiệm của phương trình (1) bằng số giao điểm của đồ thị hàm số và đường thẳng . (0,5 đi ểm )
Dựa vào đồ thị, ta suy ra kết quả biện luận về số nghiệm của phương trình (1) như sau:
 + : Phương trình (1) có 1 nghiệm. (0,5 đi ểm )
 + : Phương trình (1) có 3 nghiệm.
 + : Phương trình (1) có 2 nghiệm (0,5 đi ểm )
Câu 2 (2,0 điểm). 
 + 
 + (0,5 đi ểm )
 + (0,5 đi ểm )
 + (0,5 đi ểm )
 + (0,5 đi ểm )
Câu 3 (2,0 điểm). 
 + (0,5 đi ểm )
 + H àm số có CĐ và CT
 (0,5 đi ểm )
 + 
 + (0,5 đi ểm )
 (0,5 đi ểm )