Đề kiểm tra 1 tiết (chương V, Đại số và giải tích 11 nâng cao)
Người ra đề: VƯƠNG ĐÌNH SƠN
Đơn vị: THPT ĐINH CHƯƠNG DƯƠNG
bài soạn: Đề kiểm tra 1 tiết
(chương V,đại số và giảI tích 11 Nâng cao)
Thời gian làm bài: 45 phút
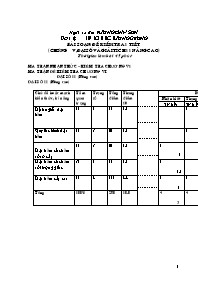
MA TRẬN NHẬN THỨC – KIỂM TRA CHƯƠNG V1 MA TRẬN ĐỀ KIỂM TRA CHƯƠNG VI
ĐẠI SỐ 11 (Nâng cao) ĐẠI SỐ 11 (Nâng cao)
Bạn đang xem tài liệu "Đề kiểm tra 1 tiết (chương V, Đại số và giải tích 11 nâng cao)", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Ngêi ra ®Ò: VƯƠNG ĐÌNH SƠN
§¬n vÞ: THPT ĐINH CHƯƠNG DƯƠNG
bµi so¹n: §Ò kiÓm tra 1 tiÕt
(ch¬ng V,®¹i sè vµ gi¶I tÝch 11 N©ng cao)
Thêi gian lµm bµi: 45 phót
MA TRẬN NHẬN THỨC – KIỂM TRA CHƯƠNG V1 MA TRẬN ĐỀ KIỂM TRA CHƯƠNG VI
ĐẠI SỐ 11 (Nâng cao) ĐẠI SỐ 11 (Nâng cao)
Chủ đề hoặc mạch kiến thức, kĩ năng
Tầm quan trọng
Trọng số
Tổng điểm
Thang điểm 10
Mức độ nhận thức
Tổng
Nhận biết
Thông hiểu
Vận dụng
KN cao hơn
Tự luận
Tự luận
Tự luận
Tự luận
Định nghĩa đạo hàm
10
2
20
0.7
1
1
1
1
Quy tác tính đạo hàm
20
3
60
2.1
1
1
1
1
2
2
Đạo hàm các hàm số sơ cấp
20
3
60
2.1
1
1
1
1
2
2
Đạo hàm các hàm số lượng giác
30
1
20
0.7
2
0.5
2
1
Đạo hàm cấp cao
10
4
120
4.4
1
1
2
1
1
1
4
4
Tổng
100%
280
10.0
4
3
4
4
2
2
1
1
11
10
I. Ma trËn thiÕt kÕ ®Ò kiÓm tra.
Møc ®é
Chñ ®Ò
NhËn biÕt
Th«ng hiÓu
VËn dông
Tæng
TNKQ
TL
TNKQ
TL
TNKQ
TL
Kh¸i niÖm ®¹o hµm
1
0,5
1
0,5
2
1,0
C¸c quy t¾c tÝnh ®¹o hµm.§¹o hµm cña hµm hîp
1
0,5
1
2
1
2
3
4,5
§¹o hµm cña hµm sè lîng gi¸c
1
0,5
1
1
1
1
3
2,5
Vi ph©n
1
0,5
1
0,5
2
2,5
§¹o hµm cÊp cao
1
0,5
1
0,5
2
1
Tæng
6
3,5
3
3,5
3
3
12
10
II. Néi dung ®Ò kiÓm tra.
A. PhÇn tr¾c nghiÖm kh¸ch quan (4 ®iÓm, mçi c©u 0,5 ®iÓm )
Trong mçi c©u tõ 1 ®Õn 8 ®Òu cã bèn ph¬ng ¸n tr¶ lêi A,B,C,D ,trong ®ã chØ cã mét ph¬ng ¸n ®óng .H·y chän ph¬ng ¸n ®óng
C©u 1. §¹o hµm cña hµm sè y = lµ :
A. 3x2 ; B. x2 ; C. 3x ; D. x
C©u 2. HÖ sè gãc cña tiÕp tuyÕn cña hµm sè y = 2x2 t¹i ®iÓm cã hoµnh ®é -1/2 lµ :
A. 4 ; B. -2 ; C. 2 ; D. - 4
C©u 3. §¹o hµm cña hµm sè y = lµ :
A. ; B. ; C. ; D.
C©u 4. Hµm sè cã ®¹o hµm b»ng sin2x lµ :
A. y = sin2x ; B. y = cos2x ; C. y = cos2x ; D. y = - sin2x
C©u 5. Cho hµm sè y = .Khi ®ã, vi ph©n cña nã lµ :
A. dy = ; B. dy = ;
C. dy = ; D. dy =
C©u 6. Gi¸ trÞ gÇn ®óng cña sin(- 0,00002) , lµm trßn kÕt qu¶ ®Õn 5 ch÷ sè thËp ph©n lµ :
A. 0 ; B. 0,00002 C. - 0,00002 D. 0,0002
C©u 7 . Cho hµm sè y = - x5 . Khi ®ã y’’’(- 1) b»ng :
A. 120 ; B. 0 ; C. – 120 ; D. Mét kÕt qu¶ kh¸c
C©u 8. §¹o hµm cÊp 2007 cña hµm sè y = sinx lµ :
A. – cosx ; B. sinx ; C. – sinx ; D. cosx
B. PhÇn tù luËn (6 ®iÓm)
C©u 9 (2 ®iÓm). Cho hµm sè f(x) = acosx + 2sinx – 3x + 1
a). T×m f’(x) ;
b). T×m a ®Ó ph¬ng tr×nh f’(x) = 0 cã nghiÖm .
C©u 10 (4 ®iÓm). Cho hµm sè f(x) =
a) . TÝnh f’( 5) ;
b). Gi¶i vµ biÖn luËn ph¬ng tr×nh f(x). f’(x) = m
III. §¸p ¸n.
C©u 1 . B C©u 5 . C
C©u 2 . B C©u 6 . B
C©u 3 . C C©u 7 . A
C©u 4 . A C©u 8 . D
C©u 9 .
f’(x) = - asinx + 2cosx – 3
Ph¬ng tr×nh f’(x) = 0 - asinx + 2cosx – 3 = 0
- asinx + 2 cosx = 3 (1)
Ph¬ng tr×nh (1) cã nhgiÖm a2 + 22 32
a2 5
{a{
VËy ®iÒu kiÖn ®Ó ph¬ng tr×nh ®· cho cã nhgiÖm lµ {a{ .
C©u 10 .
. f’(5) = ;
§Ó hµm sè ®· cho cã ®¹o hµm th× ph¶i cã x2 – 2x – 8 > 0
x 4 .
Víi ®iÒu kiÖn nµy, ta cã :
f’(x) =
Ph¬ng tr×nh
f(x).f’(x) = m
KÕt luËn :
+) Víi {m{ 3 th× ph¬ng tr×nh ®· cho v« nhgiÖm.
+) Víi {m{ > 3 th× ph¬ng tr×nh ®· cho cã nghiÖm lµ x = 1 + m .
Tài liệu đính kèm:
 De thi.doc
De thi.doc





