Chuyên đề Các bài toán cơ bản có liên quan đến vấn đề khảo sát hàm số
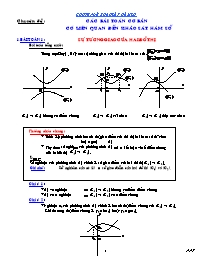
Phương pháp chung:
* Thiết lập phương trình hoành độ giao điểm của đồ thị hai hàm số đã cho: f(x) = g(x) (1)
* Ty theo số nghiệm của phương trình (1) mà ta kết luận về số điểm chung của hai đồ thị (C1) và (C2) .
Lưu ý:
Số nghiệm của phương trình (1) chính là số giao điểm của hai đồ thị (C1) và (C2).
Ghi nhơ: Số nghiệm của pt (1) = số giao điểm của hai đồ thị (C1) và (C2).
Bạn đang xem 20 trang mẫu của tài liệu "Chuyên đề Các bài toán cơ bản có liên quan đến vấn đề khảo sát hàm số", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Chuyên đề : CÁC BÀI TOÁN CƠ BẢN CÓ LIÊN QUAN ĐẾN KHẢO SÁT HÀM SỐ 1.BÀI TOÁN 1 : SỰ TƯƠNG GIAO CỦA HAI ĐỒ THỊ Bài toán tổng quát: Trong mp(Oxy) . Hãy xét sự tương giao của đồ thị hai hàm số : (C1) và (C2) không có điểm chung (C1) và (C2) cắt nhau (C1) và (C2) tiếp xúc nhau Phương pháp chung: * Thiết lập phương trình hoành độ giao điểm của đồ thị hai hàm số đã cho: f(x) = g(x) (1) * Tùy theo số nghiệm của phương trình (1) mà ta kết luận về số điểm chung của hai đồ thị (C1) và (C2) . Lưu ý: Số nghiệm của phương trình (1) chính là số giao điểm của hai đồ thị (C1) và (C2). Ghi nhớ: Số nghiệm của pt (1) = số giao điểm của hai đồ thị (C1) và (C2). Chú ý 1 : * (1) vô nghiệm (C1) và (C2) không có điểm điểm chung * (1) có n nghiệm (C1) và (C2) có n điểm chung Chú ý 2 : * Nghiệm x0 của phương trình (1) chính là hoành độ điểm chung của (C1) và (C2). Khi đó tung độ điểm chung là y0 = f(x0) hoặc y0 = g(x0). Áp dụng: Dạng 1: Tìm tọa độ giao điểm của hai đồ thị Bài 1: Tìm tọa độ giao điểm của đường cong (C): và đường thẳng Bài 2: Tìm tọa độ giao điểm của hai đường cong (C): và (C'): Bài 3: Tìm tọa độ giao điểm của đường cong (C): và đường thẳng Bài 4: Tìm tọa độ giao điểm của đường cong (C): và đường thẳng Bài 5: Tìm tọa độ giao điểm của đường cong (C): và đường thẳng Dạng 2: Tìm tham số để hai đồ thị cắt nhau tại 2( 3, 4) điểm phân biệt Bài 1 : Cho hàm số . Chứng minh rằng với mọi m, đường thẳng luơn cắt đồ thị hàm số đã cho tại hai điểm phân biệt. Bài 2 : Cho hàm số . Tìm tất cả các giá trị của tham số m để đường thẳng cắt đồ thị hàm số đã cho tại hai điểm phân biệt. Bài 3: Cho hàm số (1) Xác định m sao cho đồ thị hàm số (1) cắt trục hoành tại 3 điểm phân biệt. Bài 4: Cho hàm số (1) Xác định m sao cho đồ thị hàm số (1) cắt trục hoành tại 3 điểm phân biệt. Bài 5: Cho hàm số (1) Xác định m sao cho đồ thị hàm số (1) cắt trục hoành tại 4 điểm phân biệt. b. Điều kiện tiếp xúc của đồ thị hai hàm số : Định lý : (C1) tiếp xúc với (C1) hệ :có nghiệm Bài 1: Chứng minh rằng hai đường cong và tiếp xúc nhau.tại một điểm nào đĩ. Bài 2: Tìm k để đường thẳng tiếp xúc với đường cong Bài 3: Tìm k để đường thẳng tiếp xúc với đường cong Bài 4: Tìm k để đường thẳng tiếp xúc với đường cong Bài 2: Tìm k để đường thẳng tiếp xúc với đường cong 2.BÀI TOÁN 2: TIẾP TUYẾN VỚI ĐƯỜNG CONG a. Dạng 1: Viết phương trình tiếp tuyến với đồ thị (C):y = f(x) tại điểm (C): y=f(x) Phương pháp: Phương trình tiếp tuyến với (C) tại M(x0;y0) có dạng: y - y0 = k ( x - x0 ) hay Trong đó : x0 : hoành độ tiếp điểm y0: tung độ tiếp điểm và y0 = f(x0) k : hệ số góc của tiếp tuyến và được tính bởi công thức : k = f'(x0) Áp dụng: Bài 1: Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm trên đồ thị cĩ hồnh độ . Bài 2: Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm trên đồ thị cĩ hồnh độ . Bài 3: Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm trên đồ thị cĩ hồnh độ . Bài 4: Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm trên đồ thị cĩ tung độ . Bài 5: Cho hàm số (1). Viết phương trình tiếp tuyến với đồ thị (C) của hàm số (1) tại điểm trên (C) cĩ hồnh , biết rằng Bài 6: Cho hàm số (1). Viết phương trình tiếp tuyến với đồ thị (C) của hàm số (1) tại giao điểm của đồ thị với các trục tọa độ. b. Dạng 2: Viết phương trình tiếp tuyến với đồ thị (C): y=f(x) biết tiếp tuyến có hệ số góc k cho trước (C): y=f(x) Phương pháp: Ta có thể tiến hành theo các bước sau Bước 1: Gọi là tiếp điểm của tiếp tuyến với (C) Bước 2: Tìm x0 bằng cách giải phương trình : , từ đó suy ra =? Bước 3: Thay các yếu tố tìm được vào pt: y - y0 = k ( x - x0 ) ta sẽ được pttt cần tìm. Ví dụ: Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến cĩ hệ số gĩc Ví dụ: Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến cĩ hệ số gĩc bằng Chú ý : Đối với dạng 2 người ta có thể cho hệ số góc k dưới dạng gián tiếp như : tiếp tuyến song song, tiếp tuyến vuông góc với một đường thẳng cho trước . (C): y=f(x) (C): y=f(x) Khi đó ta cần phải sử dụng các kiến thức sau: Định lý 1: Nếu đường thẳng () có phương trình dạng : y= ax+b thì hệ số góc của () là: Định lý 2: Trong mp(Oxy) cho hai đường thẳng . Khi đó: Áp dụng: Bài 1: Cho đường cong (C): Viết phương trình tiếp tuyến với (C) biết tiếp tuyến song song với đường thẳng (d): y = 4x+2. Bài 2: Cho đường cong (C): Viết phương trình tiếp tuyến với (C) biết tiếp tuyến song song với đường thẳng Bài 3: Cho đường cong (C): Viết phương trình tiếp tuyến với (C) biết tiếp tuyến vuông góc với đường thẳng c. Dạng 3: Viết phương trình tiếp tuyến với (C): y=f(x) biết tiếp tuyến đi qua điểm A(xA;yA) Phương pháp: Ta có thể tiến hành theo các bước sau Bước 1: Viết phương trình đường thẳng () qua A và có hệ số góc là k bởi công thức: (*) Bước 2: Định k để () tiếp xúc với (C). Ta có: Bước 3: Giải hệ (1) tìm k. Thay k tìm được vào (*) ta sẽ được pttt cần tìm. Áp dụng: Ví dụ1: Cho đường cong (C): Viết phương trình tiếp tuyến với (C) biết tiếp tuyến đi qua điểm A(0;-1) Ví dụ 2: Cho đường cong (C): Viết phương trình tiếp tuyến với (C) biết tiếp tuyến đi qua điểm A(-2;0). 3.BÀI TOÁN 3: BIỆN LUẬN SỐ NGHIỆM CỦA PHƯƠNG TRÌNH BẰNG ĐỒ THỊ Cơ sở của phương pháp: Xét phương trình f(x) = g(x) (1) Nghiệm x0 của phương trình (1) chính là hoành độ giao điểm của (C1):y=f(x) và (C2):y=g(x) Bài tốn : Bằng đồ thị hãy biện luận theo m số nghiệm của phương trình dạng : f(x) = m (*) Phương pháp: Bước 1: Xem (*) là phương trình hoành độ giao điểm của hai đồ thị: Bước 2: Vẽ (C) và () lên cùng một hệ trục tọa độ Bước 3: Biện luận theo m số giao điểm của () và (C) Từ đó suy ra số nghiệm của phương trình (*) Minh họa: Áp dụng: Bài 1: 1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số 2) Dựa vào đồ thị (C), biện luận theo m số nghiệm của phương trình: 3) Tìm m để phương trình sau có 3 nghiệm phân biệt: Bài 2: 1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số 2) Dựa vào đồ thị (C), biện luận theo m số nghiệm của phương trình: Bài 3: 1) Khảo sát sự biến thiên và vẽ đồ thị hàm số 2) Tìm m để phương trình sau cĩ 4 nghiệm phân biệt: Nội dung thực hiện Yêu cầu kiến thức Khảo sát sự biến thiên và vẽ đồ thị hàm số . Biện luận số nghiệm phương trình , số giao điểm giữa hai đồ thị . Phương trình tiếp tuyến tại một điểm cho trước . Phương trình tiếp tuyến biết hệ số gĩc . Phương trình tiếp tuyến đi qua một điểm . Phương trình tiếp tuyến song song với một đường thẳng cho trước . Phương trình tiếp tuyến vuơng gĩc với một đường thẳng cho trước . Một số dạng tốn liên quan đến đơn điệu , cực trị , giá trị lớn nhất ,giá trị nhỏ nhất và đồ thị chứa dấu giá trị tuyệt đối . Yêu cầu đối với học sinh Phải bảo đảm tất cả mọi học sinh đều thành thạo trong việc khảo sát và vẽ được đồ thị ba hàm số theo đúng mẫu của SGD gởi đến. Phải bảo đảm mọi học sinh thực hiện tốt các bài tốn liên quan đến khảo sát hàm số . Phải thường xuyên ơn tập cho học sinh (Bằng cách ra đề tương tự bắt học sinh làm tại nhà ). Sơ đồ chi tiết khảo sát sự biến thiên và vẽ đồ thị hàm đa thức 1. Hàm bậc ba : y = ax3 + bx2 + cx + d (a ¹ 0) a. TXĐ : D = R b. Sự biến thiên : +. Chiều biến thiên: Đạo hàm y’ = A x2 + Bx + C ( Tính ) , Sau đây là các khả năng có thể xẩy ra : TH1: Þ y’ < 0 với mọi xR Þ HS nghịch biến trên R (1) TH2: Þ y’ > 0 với mọi xR Þ HS đồng biến trên R (2) TH3: Þ y’ £ 0 với mọi xR Þ HS nghịch biến trên R (3) TH4: Þ y’ ³ 0 với mọi xR Þ HS đồng biến trên R (4) TH5, 6: > 0 . Cho y’= 0 Û (5) và (6) Căn cứ vào BBT để kết luận các khoảng mà hàm số tăng hoặc giảm +. Cực trị : * Các TH1, TH2, TH3, TH4 : Kết luận không có cực trị * TH5: Hàm số đạt cực đại tại x = x1 và yCĐ = f(x1) Hàm số đạt cực tiểu tại x = x2 và yCT = f(x2) * TH6: Hàm số đạt cực tiểu tại x = x1 và yCT = f(x1) Hàm số đạt cực đại tại x = x2 và yCĐ = f(x2) +. Giới hạn: a > 0 : -¥ , + ¥ ; a < 0 : +¥ , - ¥ +. Bảng biến thiên : (Ứng với các trường hợp đạo hàm phía trên ) _ _ c. Đồ thị : +. Điểm đặc biệt : Tìm gđ của đồ thị (C) với Ox và Oy; điểm CT ; lấy thêm vài điểm khác +. Vẽ đồ thị : Gồm các bước : Vẽ hệ trục ; Lấy điểm đặc biệt ; Vẽ đồ thị . (Các dạng đồ thị ) 2. Hàm trùng phương : y = ax4 + bx2 + c (a ¹ 0 ) a. TXĐ : D = R b. Sự biến thiên: +. Chiều biến thiên: Đạo hàm y’ = 4ax3 + 2bx = x (4ax2 + 2b). Có thể xẩy ra 1 trong 4 trường hợp sau: TH1: Nếu a < 0 và b < 0 thì y’= 0 Û x = 0 Þ y = f(0) . Xem BBT để kết luận khoảng tăng , giảm (1) TH2: Nếu a > 0 và b > 0 thì y’= 0 Û x = 0 Þ y = f(0) . Xem BBT để kết luận khoảng tăng , giảm (2) TH3: Nếu a 0 thì y’= 0 Û . Xem BBT để kết luận khoảng tăng , giảm (3) TH4: Nếu a > 0 và b < 0 thì y’= 0 Û . Xem BBT để kết luận khoảng tăng , giảm (4) +. Cực trị : TH 1: Hàm số đạt cực đại tại x = 0 và yCĐ = f(0) TH 2: Hàm số đạt cực tiểu tại x = 0 và yCT = f(0) TH 3: Xem BBT để kết luận TH 4: Xem BBT để kết luận +. Giới hạn: a> 0 : +¥ và + ¥ ; a< 0 : -¥ và - ¥ +. Bảng biến thiên : y’ x y + 0 0 _ CĐ f(0) (1) y’ x y + 0 0 _ CT f(0) (2) y’ x y + 0 _ (3) x1 0 0 0 x2 + _ CT f(0) 0 y’ x y + 0 _ CĐ f(0) (4) x1 0 0 0 x2 + _ 0 c. Đồ thị : * Điểm đặc biệt : Tương tự như HS bậc ba * Vẽ đồ thị : Thứ tự các bước vẽ như HS bậc ba. Các dạng đồ thị của hàm trùng phương ứng với các trường hợp như sau : 3. Hàm nhất biến : y = ( c ¹ 0 ; ad –bc ¹ 0 ) a. TXĐ : D = R \ b. Sự biến thiên: +. Chiều biến thiên: Đạo hàm : y’ = . Có thể xẩy ra 1 trong 2 trường hợp sau : TH1: ad - bc > 0 Þ y’> 0 với mọi xỴDÞ HS tăng trên 2 khoảng: (-¥,);(,+¥ ) (1) TH2: ad - bc < 0 Þ y’< 0 với mọi xỴDÞ HS giảm trên 2 khoảng: (-¥,);(,+¥ ) (2) +. Cực trị: Không có +. Tiệm cận : ( có TCĐ và TCN ) * y’ > 0 : và Þ đường thẳng x = là TCĐ y’ < 0 : va Þ đường thẳng x = là TCĐ * Þ đường thẳng y = là TCN +. Bảng biến thiên : _ _ c. Đồ thị : * Điểm đặc biệt : Tìm giao điểm của đồ thị với các trục toạ độ ; lấy thêm vài điểm khác * Vẽ đồ thị : Gồm các bước : Ve ... . Cho hàm số (C) Khảo sát và vẽ đồ thị (C) của hàm số . Biện luận theo m số nghiệm thực của phương trình Viết phương trình tiếp tuyến của đồ thị (C) tại điểm cĩ tung độ . Viết phương trình tiếp tuyến của đồ thị (C) , biết hệ số gĩc của tiếp tuyến bằng 2. Tìm các điểm trên trục tung sao cho từ đĩ kẻ được 3 tiếp tuyến đến (C) . Bài 5. Cho hàm số (C) Khảo sát và vẽ đồ thị (C) của hàm số . Tìm m để phương trình cĩ 4 nghiệm thực phân biệt. Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến song song với đường thẳng . Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến vuơng gĩc với đường thẳng . Viết phương trình parabol đi qua các điểm cực trị của đồ thị (C) . Bài 6. Cho hàm số (C) Khảo sát và vẽ đồ thị (C) của hàm số . Tìm m để phương trình cĩ 2 nghiệm thực phân biệt . Viết phương trình tiếp tuyến của (C) tại điểm cĩ hồnh độ . Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến vuơng gĩc với đường thẳng . Viết phương trình đường thẳng đi qua điểm và tiếp xúc với đồ thị (C) . Bài 7. Cho hàm số (C) Khảo sát và vẽ đồ thị (C) của hàm số . Dựa vào đồ thị (C) , hãy giải bất phương trình . Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của (C) với trục tung . Viết phương trình tiếp tuyến của đồ thị (C) tại điểm cĩ tung độ bằng 3 . Tìm m để đường thẳng cắt đồ thị (C) tại 4 điểm phân biệt . Bài 8. Cho hàm số Khảo sát và vẽ đồ thị (C) của hàm số khi . Biện luận theo k số nghiệm thực của phương trình . Dựa vào đồ thị (C) , hãy giải bất phương trình . Tìm m để hàm số (1) đạt cực tiểu tại . Tìm m để hàm số (1) cĩ 3 cực trị . Bài 9. Cho hàm số Khảo sát và vẽ đồ thị (C) của hàm số khi . Biện luận theo k số nghiệm thực của phương trình . Tìm m để hàm số đạt cực tiểu tại . Tìm m để hàm số cĩ 1 cực trị . Tìm m để hàm số (1) cĩ 3 điểm cực trị và 3 điểm cực trị đĩ lập thành một tam giác cĩ một gĩc 1200 . Bài 10. Cho hàm số (1) Khảo sát và vẽ đồ thị (C) của hàm số khi . Tìm k để phương trình cĩ hai nghiệm thực phân biệt . Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến vuơng gĩc với đường thẳng . Tìm m để hàm số cĩ một điểm cực trị . Tìm m để hàm số cĩ ba điểm cực trị . c. Hàm số hữu tỉ Bài 1. Cho hàm số (C) Khào sát và vẽ đồ thị (C) của hàm số . Viết phương trình tiếp tuyến của (C) tại điểm cĩ hồnh độ . Viết phương trình tiếp tuyến của (C) tại điểm cĩ tung độ . Viết phương trình tiếp tuyến của (C) , biết hệ số gĩc của tiếp tuyến . Tìm m để đường thẳng cắt (C) tại 2 điểm phân biệt . Bài 2. Cho hàm số (C) Khào sát và vẽ đồ thị (C) của hàm số . Viết phương trình tiếp tuyến của (C) tại điểm cĩ tung độ . Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến song song với đường thẳng . Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến vuơng gĩc với đường thẳng . Tìm m để đường thẳng cắt đồ thị (C) tại 2 điểm phân biệt cĩ hồnh độ âm . Bài 3. Cho hàm số (C) Khào sát và vẽ đồ thị (C) của hàm số . Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) và trục hồnh . Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) và trục tung . Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến vuơng gĩc với đường thẳng . Tìm m để đường thẳng cắt đồ thị (C) tại 2 điểm phân biệt cĩ hồnh độ dương . Bài 4. Cho hàm số (C) Khào sát và vẽ đồ thị (C) của hàm số . Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến song song với đường phân giác của gĩc phần tư thứ nhất . Tìm m để đường thẳng cắt đồ thị (C) tại hai điểm A, B phân biệt .Tìm tập hợp trung điểm I của đoạn thẳng AB . Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến vuơng gĩc với đường thẳng . Tìm những điểm trên đồ thị (C) cĩ toạ độ với hồnh độ và tung độ đều là số nguyên . Bài 5. Cho hàm số (C) Khào sát và vẽ đồ thị (C) của hàm số . Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến vuơng gĩc với đường phân giác của gĩc phần tư thứ hai . Viết phương trình đường thẳng qua điểm và tiếp xúc với đồ thị (C) . Tìm m để đường thẳng đồ thị (C) tại hai điểm A, B phân biệt .Tìm tập hợp trung điểm I của đoạn thẳng AB . Tìm những điểm trên đồ thị (C) cĩ toạ độ với hồnh độ và tung độ đều là số nguyên . Bài 6. Cho hàm số (C) Khào sát và vẽ đồ thị (C) của hàm số . Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến song song với đường phân giác của gĩc phần tư thứ hai . Viết phương trình đường thẳng qua điểm và tiếp xúc với đồ thị (C) . Tìm những điểm trên đồ thị (C) cĩ toạ độ với hồnh độ và tung độ đều là số nguyên . Chứng minh rằng tích các khoảng cách từ một điểm bất kỳ trên (C) đến hai đường tiệm cận của (C) là một hằng số . Bài 7. Cho hàm số (C) Khào sát và vẽ đồ thị (C) của hàm số . Tìm m để đường thẳng cắt đồ thị (C) tại hai điểm phân biệt A, B . Tìm tập hợp trung điểm I của đoạn thẳng AB . Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên . Viết phương trình đường thẳng qua điểm và tiếp xúc với đồ thị (C) . Chứng minh rằng tích các khoảng cách từ một điểm bất kỳ trên (C) đến hai đường tiệm cận của (C) là một hằng số . Bài 8. Cho hàm số (C) Khào sát và vẽ đồ thị (C) của hàm số . Dựa vào đồ thị (C), biện luận theo m số giao điểm của đồ thị (C) và đường thẳng . Viết phương trình tiếp tuyến của (C) tại các giao điểm của (C) và đường thẳng . Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên . Tìm trên đồ thị (C) hai điểm đối xứng nhau qua đường thẳng . Bài 9. Cho hàm số (C) Khào sát và vẽ đồ thị (C) của hàm số . Tìm những điểm trên (C) sao cho khoảng từ điểm đĩ đến trục hồnh gấp đơi khoảng cách từ đĩ đến trục tung . Viết phương trình tiếp tuyến của (C) tại những điểm tìm được ở câu 2 . Tìm tất cả các tâm đối xứng của đồ thị (C) . Tìm m để phương trình cĩ nghiệm . Bài 10. Cho hàm số (C) Khào sát và vẽ đồ thị (C) của hàm số . Tìm toạ độ những điểm M sao cho . Viết phương trình tiếp tuyến của (C) tại những điểm tìm được ở câu 2 . Chứng tỏ giao điểm hai đường tiệm cận là tâm đối xứng của đồ thị (C) . Tìm m để phương trình cĩ 4 nghiệm phân biệt . BÀI GIẢI a. Hàm số bậc ba Bài 1. Cho hàm số (C) Khảo sát và vẽ đồ thị (C) của hàm số . Dựa vào đồ thị (C) , biện luận theo m số nghiệm của phương . Viết phương trình tiếp tuyến của (C) tại điểm . Viết phương trình tiếp tuyến của (C) tại điểm cĩ hồnh độ . Viết phương trình của (C) tại các điểm cĩ tung độ là 0 . Đáp án: CÂU ĐÁP ÁN ĐIỂM CÂU 1 (x điểm) 1. (điểm) 1) Tập xác định: 2) Sự biến thiên a) Giới hạn và b) Bảng biến thiên Bảng biến thiên: x y’ y -¥ -1 1 +¥ 0 0 + - + 4 +¥ -¥ 0 Hàm số đồng biến trên các khoảng và , nghịch biến trên khoảng. Hàm số đạt cực đại tại , , đạt cực tiểu tại , . 3) Đồ thị Điểm uốn: (chương trình chuẩn khơng học) Do y'' đổi dấu khi x đi qua Tọa độ điểm uốn Giao điểm của đồ thị với các trục tọa độ + Giao điểm với Oy: : + Giao điểm với Ox: Nhận xét: Đồ thị nhận điểm uốn làm tâm đối xứng. 2. (điểm) Số nghiệm thực của phương trình bằng số giao điểm của đồ thị (C) của hàm số và đừờng thẳng (d): . Dựa vào đồ thị ta cĩ: Với hoặc , (d) và (C) cĩ một điểm chung, do đĩ phương trình cĩ một nghiệm. Với hoặc , (d) và (C) cĩ hai điểm chung, do đĩ phương trình cĩ hai nghiệm. Với , (d) và (C) cĩ ba điểm chung, do đĩ phương trình cĩ ba nghiệm. 3. (điểm) Hệ số gĩc của tiếp tuyến tại điểm là . Phương trình tiếp tuyến của (C) tại điểm M là . 4. (điểm) Điểm thuộc đồ thị hàm số cĩ hồnh độ , cĩ tung độ . Hệ số gĩc của tiếp tuyến tại tiếp điểm là Phương tình tiếp tuyến của (C) tại điểm là . 5. (điểm) Điểm thuộc (C) cĩ tung độ , cĩ hồnh độ hoặc . Hệ số gĩc của tiếp tuyến tại điểm là . Phương trình của hai tiếp tuyến của (C) tại điểm cĩ tung độ bằng 0 là và . b. Hàm số trùng phương Bài 1. Cho hàm số (C) Khảo sát và vẽ đồ thị (C) của hàm số . Biện luận theo m số nghiệm thực của phương trình Viết phương trình tiếp tuyến của đồ thị (C) tại điểm cĩ hồnh độ . Viết phương trình tiếp tuyến của đồ thị (C) tại điểm cĩ tung độ . Viết phương trình tiếp tuyến của đồ thị (C) , biết hệ số gĩc của tiếp tuyến bằng 24 . Đáp án: CÂU ĐÁP ÁN ĐIỂM CÂU 1 (x điểm) 1. (điểm) 1) Tập xác định: 2) Sự biến thiên a) Giới hạn b) Bảng biến thiên và Bảng biến thiên: x y’ y -¥ -1 1 +¥ 0 0 + – + -1 +¥ +¥ 0 0 – -1 Hàm số đồng biến trên các khoảng và , nghịch biến trên các khoảng và . Hàm số đạt cực đại tại , , đạt cực tiểu tại , . 3) Đồ thị Điểm uốn: (chương trình chuẩn khơng học) Do y'' đổi dấu khi x đi qua Tọa độ điểm uốn Giao điểm của đồ thị với các trục tọa độ + Giao điểm với Oy: : + Giao điểm với Ox: Nhận xét: Hàm số đã cho là hàm số chẵn nên đồ thị của nĩ nhận trục tung làm trục đối xứng. 2. (điểm) Số nghiệm thực của phương trình bằng số giao điểm của đồ thị (C) của hàm số và đường thẳng (d): . Dựa vào đồ thị ta cĩ: Với , (d) và (C) khơng cĩ điểm chung, do đĩ phương trình vơ nghiệm. Với hoặc , (d) và (C) cĩ hai điểm chung, do đĩ phương trình cĩ hai nghiệm. Với , (d) và (C) cĩ bốn điểm chung, do đĩ phương trình cĩ bốn nghiệm. 3. (điểm) Tung độ của tiếp tuyến tại điểm cĩ hồnh độ là Hệ số gĩc của tiếp tuyến tại điểm là . Phương trình tiếp tuyến của (C) tại điểm là . 4. (điểm) Điểm thuộc đồ thị hàm số cĩ tung độ , cĩ hồnh độ . Hệ số gĩc của tiếp tuyến tại tiếp điểm và lần lượt là , . Phương tình tiếp tuyến của (C) tại điểm là và tại điểm là . 5. (điểm) Điểm thuộc (C) cĩ hệ số gĩc tiếp tuyến tại M là . Khi đĩ, ta cĩ: Lúc này tung độ của M là . Phương trình tiếp tuyến của (C) tại điểm M là . c. Hàm số hữu tỉ Bài 1. Cho hàm số (C) Khào sát và vẽ đồ thị (C) của hàm số . Viết phương trình tiếp tuyến của (C) tại điểm cĩ hồnh độ . Viết phương trình tiếp tuyến của (C) tại điểm cĩ tung độ . Viết phương trình tiếp tuyến của (C) , biết hệ số gĩc của tiếp tuyến . Tìm m để đường thẳng cắt (C) tại 2 điểm phân biệt . Đáp án: CÂU ĐÁP ÁN ĐIỂM CÂU 1 (x điểm) 1. (điểm) 1) Tập xác định: 2) Sự biến thiên a) Giới hạn và là tiệm cận đứng và là tiệm cận ngang b) Bảng biến thiên Bảng biến thiên: x y’ y -¥ -1 +¥ 2 + + +¥ -¥ 2 Hàm số đồng biến trên các khoảng và . Hàm số khơng cĩ cực trị. 3) Đồ thị Giao điểm của đồ thị với các trục tọa độ + Giao điểm với Oy: : + Giao điểm với Ox: Nhận xét: Đồ thị nhận giao điểm của hai tiệm cận làm tâm đối xứng. 2. (điểm) Điểm thuộc đồ thị hàm số cĩ hồnh độ , cĩ tung độ . Hệ số gĩc của tiếp tuyến tại tiếp điểm là Phương tình tiếp tuyến của (C) tại điểm là . 3. (điểm) Điểm thuộc đồ thị hàm số cĩ tung độ , cĩ hồnh độ , Hệ số gĩc của tiếp tuyến tại tiếp điểm là . Phương tình tiếp tuyến của (C) tại điểm là . 4. (điểm) Điểm thuộc đồ thị (C), cĩ hệ số gĩc của tiếp tuyến tại M là . Khi đĩ, ta cĩ: hoặc . Tung độ của điểm M là hoặc . Vậy cĩ hai tiếp tuyến cĩ phương trình là và . 5. (điểm) Tìm m để đường thẳng cắt (C) tại 2 điểm phân biệt . Đường thẳng (d) cắt (C) tại 2 điểm phân biệt khi phương trình: (1) cĩ hai nghiệm phân biệt và khác –1. , (1) (2) Ta thấy (2) khơng cĩ nghiệm . Khi đĩ (2) cĩ 2 nghiệm phân biệt khi: . Vậy thì (d) cắt (C) tại 2 điểm phân biệt.
Tài liệu đính kèm:
 CHUYENDE- KSHS-TOAN Chuong I.doc
CHUYENDE- KSHS-TOAN Chuong I.doc





