Báo cáo ôn tập Hình học không gian thi tốt nghiệp THPT - Chủ đề: Khối đa diện và khối tròn xoay
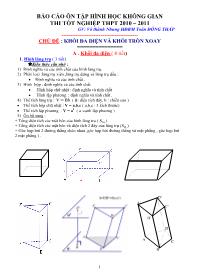
A . Khối đa diện ( 8 tiết)
I. Hình lăng trụ ( 3 tiết)
êKiến thức cần nhớ :
1) Định nghĩa và các tính chất của hình lăng trụ.
2) Phân loại :lăng trụ xiên ,lăng trụ đứng và lăng trụ đều :
· Định nghĩa và các tính chất .
3) Hình hộp : định nghĩa và các tính chất
· Hình hộp chữ nhật : định nghĩa và tính chất
· Hình lập phương : định nghĩa và tính chất .
4) Thể tích lăng trụ : V Bh = ( B: diện tích đáy, h : chiều cao )
Bạn đang xem tài liệu "Báo cáo ôn tập Hình học không gian thi tốt nghiệp THPT - Chủ đề: Khối đa diện và khối tròn xoay", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
1BÁO CÁO ÔN TẬP HÌNH HỌC KHÔNG GIAN THI TỐT NGHIỆP THPT 2010 – 2011 GV: Võ thành Nhung HĐBM Toán ĐỒNG THÁP ------------------------------------------- CHỦ ĐỀ : KHỐI ĐA DIỆN VÀ KHỐI TRÒN XOAY =============== A . Khối đa diện ( 8 tiết) I. Hình lăng trụ ( 3 tiết) êKiến thức cần nhớ : 1) Định nghĩa và các tính chất của hình lăng trụ. 2) Phân loại :lăng trụ xiên ,lăng trụ đứng và lăng trụ đều : · Định nghĩa và các tính chất . 3) Hình hộp : định nghĩa và các tính chất · Hình hộp chữ nhật : định nghĩa và tính chất · Hình lập phương : định nghĩa và tính chất . 4) Thể tích lăng trụ : V Bh= ( B: diện tích đáy, h : chiều cao ) · Thể tích hộp chữ nhật : V = a.b.c ( a,b,c : 3 kích thước) · Thể tích lập phương : V = a3 ( a :cạnh lập phương ) 5) Ôn bổ sung : + Tổng diện tích các mặt bên của hình lăng trụ ( Sxq ) + Tổng diện tích các mặt bên và diện tích 2 đáy của lăng trụ (Stp ) + Góc hợp bởi 2 đường thẳng chéo nhau ,góc hợp bởi đường thẳng và mặt phẳng , góc hợp bởi 2 mặt phẳng ) . D D’ B CA A’ B’ C’ 2a 3a C' B' A' C B A o60 C' B' A' C B A ê Các bài toán áp dụng cơ bản Hướng dẩn thực hiện ôn tậpChuẩn : Kiến thức và kĩ năng Kiến thức cơ bản Lưu ý Các dạng toán cơ bản Lưu ý + Biết tính chất và cấu tạo của khối lăng trụ đứng tam giác. + Biết dưng hình lăng trụ đứng tam giác . + Biết tính thể tích của lăng trụ đứng + Biết tính chất và cấu tạo của khối lăng trụ đứng tam giác. + Biết dựng hình lăng trụ đứng tam giác . + Biết xác định góc hợp bởi đường thẳng và mặt phẳng + Biết tính thể tích của lăng trụ đứng + Biết tính chất và cấu tạo của khối lăng trụ tứ giác đều . + Biết dựng hình lăng trụ tứ giác đều . + Biết xác định góc hợp bởi mặt + Cạnh bên lăng trụ đứng vuông góc với đáy . + Độ dài của cạnh bên là chiều cao của lăng trụ đứng + Thể tích V=B.h + Cạnh bên lăng trụ đứng vuông góc với đáy . + Góc hợp bởi đường thẳng và mặt phẳng . + Hệ thức lương giác trong tam giác vuông . + Diện tích tam giác vuông + Thể tích V=B.h + Lăng trụ đều là lăng trục đứng có đáy đa giác đều . + Cạnh bên lăng trụ đều vuông góc với đáy và là chiều cao của lăng trụ đều. + Góc hợp bởi mặt phẳng và mặt phẳng . Ví dụ 1 Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác ABC vuông cân tại A có cạnh BC = a 2 và biết A'B = 3a. Tính thể tích khối lăng trụ. Lời giải: Ta có ABCV vuông cân tại A nên AB = AC = a ABC A'B'C' là lăng trụ đứng AA' ABÞ ^ 2 2 2 2 AA'B AA' A 'B AB 8a Þ = - = V AA' 2a 2Þ = Vậy V = B.h = SABC .AA' = 3a 2 Ví dụ 2: Cho lăng trụ đứng tam giác ABC A'B'C' có đáy ABC là tam giác vuông cân tại B với BA = BC = a ,biết A'B hợp với đáy ABC một góc 600 .Tính thể tích lăng trụ. Lời giải: + Ta có A'A (ABC) A'A AB&AB^ Þ ^ là hình chiếu của A'B trên đáy ABC . Vậy ¼ ogóc[A 'B, (ABC)] ABA ' 60= = + 0ABA' AA' AB.tan 60 a 3Þ = =V SABC = 21 aBA.BC 2 2 = Vậy V = SABC.AA' = 3a 3 2 Ví dụ 3: Cho lăng trụ tứ giác đều ABCD A'B'C'D' có cạnh đáy a và mặt phẳng (BDC') hợp với đáy (ABCD) một góc 60o.Tính thể tích khối hộp chữ nhật. Lời giải: + Gọi O là tâm của ABCD .Ta cóABCD là hình vuông nên OC BD^ và CC'^ (ABCD) Nên OC'^BD(đl 3^ ). Vậy góc[(BDC');(ABCD)] =¼COC' = 60o Ta có V = B.h = SABCD.CC' ABCD là hình vuôngnên SABCD = a2 3a 060 O A' D' B' C' C A D B H O o60 C' A a B' A' C B 2a o 30 o60 D' C'B' A' D C B A phẳng và mặt phẳng + Biết tính thể tích của lăng trụ đều . + Biết tính chất và cấu tạo của hộp chữ nhật + Biết dựng hình hộp chữ nhật . + Biết xác định góc hợp bởi đường thẳng và mặt phẳng + Biết xác định góc hợp bởi mặt phẳng và mặt phẳng + Biết tính thể tích của hộp chử nhật . + Biết tính chất và cấu tạo của khối lăng trụ xiên tam giác. + Biết dưng hình lăng trụ xiên tam giác . + Biết xác định góc hợp bởi đường thẳng và mặt phẳng. + Biết cách chứng minh 2 đường thẳng vuông góc với nhau + Hệ thức lương giác trong tam giác vuông . + Thể tích V=B.h + Hộp chữ nhật là lăng trụ đứng có cạnh bên là chiều cao. + Góc hợp bởi đường thẳng và mặt phẳng + Góc hợp bởi mặt phẳng và mặt phẳng + Hệ thức lương giác trong tam giác vuông +Thể tích V=abc=B.h + Cạnh bên lăng trụ xiên không vuông góc với đáy . + Khoảng cách giữa 2 đáy là chiều cao của lăng trụ xiên . + Mặt bên lăng tru xiên là hình bình hành . + Điều kiện để 2 đường thẳng vuông góc nhau + Hệ thức lương giác trong tam giác vuông OCC'V vuông nên CC' = OC.tan60o = a 6 2 Vậy V = 3a 6 2 Ví dụ 4: Cho hình hộp chữ nhật ABCD A'B'C'D' có AA' = 2a ; mặt phẳng (A'BC) hợp với đáy (ABCD) một góc 60o và A'C hợp với đáy (ABCD) một góc 30o .Tính thể tích khối hộp chữ nhật. Lời giải: Ta có AA' (ABCD)^ Þ AC là hình chiếu của A'C trên (ABCD)Vậy góc[A'C,(ABCD)] = ¼ oA 'CA 30= BC ^AB ÞBC ^A'B (đl 3^ ) . Vậy góc[(A'BC),(ABCD)] =¼ oA'BA 60= A'ACÞV AC = AA'.cot30o= 2a 3 A'ABÞV AB = AA'.cot60o = 2a 3 3 2 2 4a 6ABC BC AC AB 3 Þ = - =V Vậy V = AB.BC.AA' = 316a 2 3 Ví dụ 5: Cho lăng trụ xiên tam giác ABC A'B'C' có đáy ABC là tam giác đều cạnh a . Hình chiếu của A' xuống (ABC) là tâm O đường tròn ngoại tiếp D ABC biết AA' hợp với đáy ABC một góc 60 . 1) Chứng minh rằng BB'C'C là hình chữ nhật. 2) Tính thể tích lăng trụ . Lời giải: 1) Ta có A 'O (ABC) OA^ Þ là hình chiếu của AA' trên (ABC) Vậy ¼ oóc[AA ', (ABC)] OAA ' 60g = = Ta có BB'CC' là hình bình hành ( vì mặt bên của lăng trụ) AO BC^ tại trung điểm H của BC nên BC A'H^ (đl 3 ^ ) BC (AA 'H) BC AA 'Þ ^ Þ ^ mà AA'//BB' nên BC BB'^ . Vậy BB'CC' là hình chữ nhật. 2) ABCV đều nên 2 2 a 3 a 3AO AH 3 3 2 3 = = = 4+ Biết tính thể tích của lăng trụ xiên + Hướng dẫn học sinh tự rèn luyện cũng cố chuẩn kiến thức và các kĩ năng đã được giáo viên hướng dẫn qua các ví dụ trên . + Thể tích V=B.h + Học sinh tự ôn tập , tự rèn luyện và cũng cố các kiến thức cơ bản . oAOA ' A 'O AO t an60 aÞ = =V Vậy V = SABC.A'O = 3a 3 4 LUYỆN TẬP Bài 1:Cho lăng trụ đứng ABCD.A'B'C'D' có đáy là tứ giác đều cạnh a biết rằng BD' a 6= . Tính thể tích của lăng trụ. Đs: V = 2a3 Bài 2: Cho lăng trụ đứng ABC A'B'C' có đáy ABC vuông tại B biết BB' = AB = a và B'C hợp với đáy (ABC) một góc 30o . Tính thể tích lăng trụ. ĐS: 3a 3V 2 = Bài 3: Cho lăng trụ đứng ABCD A'B'C'D' có đáy ABCD là hình vuông và cạnh bên bằng a biết rằng mặt (ABC'D') hợp với đáy một góc 30o.Tính thể tích khối lăng trụ. Đs: V = 3a3 Bài 4: Cho hình hộp chữ nhật ABCD A'B'C'D' có BD' = 5a ,BD = 3aTính thể tích khối hộp trong các trường hợp sau đây: 1) AB = a 2) BD' hợp với AA'D'D một góc 30o 3) (ABD') hợp với đáy ABCD một góc 300 Đs: 1) 3 2V 8a= ; 2) V = 3 115a ; V = 316a Bài 5: Cho lăng trụ ABC A'B'C' có đáy ABC là tam giác đều cạnh a , đỉnh A' có hình chiếu trên (ABC) nằm trên đường cao AH của tam giác ABC biết mặt bên BB'C'C hợp vớio đáy ABC một góc 60o . 1) Chứng minh rằng BB'C'C là hình chữ nhật. 2) Tính thể tích lăng trụ ABC A'B'C'. Đs: 33a 3V 8 = II. Hình Chóp ( 5 tiết) êKiến thức cần nhớ : 1) Định nghĩa và các tính chất của hình chóp. 2) Phân loại chóp n giác · Chóp đều : Định nghĩa và các tính chất . 3) Thể tích chóp : 1 3 V Bh= ( B: diện tích đáy, h : chiều cao ) 4) Tỷ số thể tích : Cho khối chóp S.ABC.A'ÎSA, B'ÎSB, C'ÎSC . . ' ' ' . . '. '. ' =S ABC S A B C V SA SB SC V SA SB SC · MÎSC, ta có: . . . . . . S ABM S ABC V SA SB SM SM V SA SB SC SC = = 4) Ôn bổ sung : + Tổng diện tích các mặt bên của hình chóp ( Sxq ) C B A S A' B' C' A C B S M S A B C D H 5a o60 M C B A S a o60 S C B A + Tổng diện tích các mặt bên và diện tích đáy của chóp ( Stp ) + Góc hợp bởi 2 đường thẳng chéo nhau ,góc hợp bởi đường thẳng và mặt phẳng , góc hợp bởi 2 mặt phẳng ) . ê Các bài toán áp dụng cơ bản Hướng dẩn thực hiện ôn tậpChuẩn : Kiến thức và kĩ năng Kiến thức cơ bản Lưu ý Các dạng toán cơ bản ( ví dụ) Lưu ý + Biết tính chất và cấu tạo của khối chóp tam giác có cạnh bên vuông góc với đáy. + Biết dựng hình + Biết xác định góc hợp bởi mặt phẳng và mặt phẳng + Biết tính thể tích của khối chóp + Biết tính chất và cấu tạo của hình chóp tam giác có cạnh bên vuông góc với đáy. + Biết dựng hình + Biết xác định góc hợp bởi đường thẳng và mặt phẳng. + Biết cách chứng minh 2 đường thẳng vuông góc . + Biết xác định tâm mặt cầu ngoại tiếp hình chóp + Biết tính thể tích của khối chóp + Hình chóp có cạnh bên vuông góc với đáy là chiều cao. + Góc hợp bởi mặt phẳng và mặt phẳng + Hệ thức lương giác trong tam giác vuông + Diện tích tam giác đều . +Thể tích V= 1 3 B.h + Hình chóp có cạnh bên vuông góc với đáy là chiều cao. + Góc hợp bởi đường thẳng và mặt phẳng . + Điều kiện để 2 đường thẳng vuông góc nhau . + Tập hợp các điểm nhìn một đoạn thẳng dưới một góc vuông. + Mặt cầu ngoại tiếp hình chóp . + Hệ thức lương giác trong tam giác vuông + Diện tích tam giác vuông . +Thể tích V= 1 3 B.h Ví dụ 1: Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy ABC và (SBC) hợp với đáy (ABC) một góc 60o.Tính thể tích hình chóp . Lời giải: M là trung điểm của BC, vì tam giác ABC đều nên AM ^BC ÞSA^BC (đl3^ ) . Vậy góc[(SBC);(ABC)] = ¼ oSMA 60= . Ta có V = ABC 1 1B.h S .SA 3 3 = o 3aSAM SA AM tan60 2 Þ = =V Vậy V = 3 ABC 1 1 a 3B.h S .SA 3 3 8 = = Ví dụ 2: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B với AC = a biết SA vuông góc với đáy ABC và SB hợp với đáy một góc 60o. 1) Chứng minh các mặt bên là tam giác vuông. Xác định tâmmặt cầu ngoại tiếp SABC 2)Tính thể tích hình chóp . Lời giải: 1) SA (ABC) SA AB &SA AC^ Þ ^ ^ mà BC AB BC SB^ Þ ^ (đl 3^ ).Vậy các mặt bên chóp là tam giác vuông. Ta có ¼SAC =¼ oSBC 90 Þ= SABC có mặt cầu ngoại tiếp có đường kính SC , tâm là trung điểm của SC 2) Ta cóSA (ABC) AB^ Þ là hình chiếu của SB trên (ABC). Vậy góc[SB,(ABC)] =¼ oSAB 60= . ABCV vuông cân nên BA = BC = a 2 SABC = 21 aBA.BC 2 4 = o a 6SAB SA AB.t an60 2 Þ = =V Vậy 2 3 ABC 1 1 a a 6 a 6V S .SA 3 3 4 2 24 = = = 6o60 a H D C B A a O D C B A S + Biết tính chất và cấu tạo của khối chóp tam giác có mặt bên vuông góc với đáy + Biết dựng hình chóp tam giác có 2 mặt vuông góc nhau + Biết xác định góc hợp bởi đường thẳng và mặt phẳng + Biết tính thể tích của khối chóp tam giác + Biết chứng minh chóp tứ giác có các cạnh bằng nhau là chóp tứ giác đều. + Biết dựng hình chóp tứ giác đều + Biết xác định đường cao của tứ giác đều . + Biết tính thể tích của khối chóp tứ giác đều + Biết tính chất và cấu tạo của khối chóp tam giác có cạnh bên vuông góc với đáy. + Biết dựng hình + Biết xác định tỉ số 2 đoạn thẳng cho bởi định lý Thalès + Hình chóp có mặt bên vuông góc với đáy . (P) (Q) theogt d và d ' (P)& d ' d thì d ' (Q) + ^ Ì ^ ^ + Góc hợp bởi đường thẳng và mặt phẳng + Hệ thức lương giác trong tam giác vuông + Diện tích tam giác vuông . +Thể tích V= 1 3 B.h + Định nghĩa và tính chất , cấu tạo của khối chóp tứ giác đều . + Đường c ... +Biết tính Sxq ; Sxq và V của hình nón + Biết cách xác định góc hợp bởi thiết diện qua đỉnh nón và mặt đáy của nón . + Biết tính diện tích thiết diện của mặt phẳng qua đỉnh với hình nón. + Biết cách xác định tâm và bán kính mặt cầu đi qua 4 đỉnh của tứ diện. + Biết tính thể tích và diện tích hình cầu . + Diện tích toàn phần hình nón : Stp = Sxq + Sđáy + Thể tích khối nón V = 2 1 3 R hp + xác định góc hợp bởi thiết diện qua đỉnh nón và mặt đáy của nón . + Hệ thức lượng giác trong tam giác vuông . + Diện tích tam giác cân . + Tập hợp các điểm cách đều một điểm cố định một độ dài không đổi. + Diện tích mặt cầu : S = 4 2Rp + Thể tích khối cầu: A Ù = B Ù = 450 * Sxq = pRl = p .OA.SA = p . 2 a .a = 2 2 ap Tính: OA = 2 a ( ÚD SOA tại O) * Stp = Sxq + Sđáy = 2 2 ap + 2 2 ap = 2 1 1 22 a+ pæ öç ÷è ø c) V = 2 1 3 R hp = 21 3 .OA .SOp = 2 31 3 2 2 6 2 a a a . . pp = Tính: SO = 2 a ( ÚD SOA tại O) c) * Thiết diện (SAC) qua trục tạo với đáy 1 góc 600: SM O Ù = 600 * Tính: SM = 6 3 a ( ÚD SMO tại O). * Tính: AC = 2AM = 2 3 3 a * Tính: AM = 2 2OA OM- = 3 3 a * Tính: OM = 6 6 a ( ÚD SMO tại O) * SSAC = 1 2 SM.AC = 1 2 . 6 3 a . 2 3 3 a = 2 2 3 a Khối Cầu Bài 1: Cho tứ diện ABCD có DA = 5a và vuông góc với mp(ABC),D ABC vuông tại B, AB=3a, BC = 4a. a) Xác định mặt cầu đi qua 4 điểm A, B, C, D b) Tính bán kính của mặt cầu nói trên. Tính diện tích và thể tích của mặt cầu HD: a) * Gọi O là trung điểm của CD. * Chứng minh: OA = OB = OC = OD; * Chứng minh: D DAC vuông tại A ÞOA = OC = OD = 1 2 CD * Chứng minh: D DBC C M 45 a S BA O 12 + Biết cách xác định tâm và bán kính mặt cầu đi qua 5 đỉnh của chóp tứ giác đều .. + Biết tính thể tích và diện tích hình cầu + Biết cách xác định tâm và bán kính mặt cầu đi qua 5 đỉnh của hình chóp + Biết tính thể tích và diện tích hình cầu . V = 3 4 R 3 p + Tập hợp các điểm cách đều một điểm cố định một độ dài không đổi. + Diện tích mặt cầu : S = 4 2Rp + Thể tích khối cầu: V = 3 4 R 3 p + Tập hợp các điểm nhìn một đoạn thẳng cố định dưới một góc vuông + Diện tích mặt cầu : S = 4 2Rp + Thể tích khối cầu: V = 3 4 R 3 p vuông tại B ÞOB = 1 2 CD * OA = OB = OC = OD = 1 2 CD Û A, B, C, D thuộc mặt cầu S(O; 2 CD ) b) Bán kính R = 2 CD = 1 2 2 2AD AC+ = 1 2 2 2 2AD AB BC+ + = 1 2 2 2 2 5 225 9 16 2 aa a a+ + = * S = 2 25 24 50 2 a a æ öp = pç ÷ è ø ; * V = 4 3 pR3 = 3 34 5 2 125 2 3 2 3 a app = æ ö ç ÷ç ÷è ø Bài 2: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. a)Xác định mặt cầu đi qua 5 điểm A, B, C, D, S b)Tính bán kính của mặt cầu nói trên. Tính diện tích và thể tích của mặt cầu HD: a) Gọi O là tâm hình vuông (đáy). Chứng minh: OA = OB = OC = OD = OS b) R = OA = 2 2 a ; S = 2a2p ; V = 3 2 3 a p Bài 3: Cho chóp S. ABCD có ABCD là hính vuông cạnh bằng a. SA = 2a và vuông góc với mp(ABCD). a) Xác định mặt cầu đi qua 5 điểm A, B, C, D, S b) Tính bán kính của mặt cầu nói trên. Tính diện tích và thể tích của mặt cầu HD: a) * Gọi O là trung điểm SC * Chứng minh: Các D SAC, D SCD, D SBC lần lượt vuông tại A, D, B * OA = OB = OC = OD = OS = 2 SC Û S(O; 2 SC ) O D C B A 2a a S O D CB A 13 a C C' O O' A1 A1' B' B I A' + Biết cách xác định tâm và bán kính mặt cầu đi qua 4 đỉnh của tứ diện. + Biết áp dụng trục đường tròn và mặt phẳng trung trực để tìm tâm hình cầu ngoại tiếp hình chóp . + Biết tính thể tích và diện tích hình cầu . + Biết cách xác định tâm và bán kính mặt cầu đi qua 6 đỉnh của lăng trụ + Biết áp dụng trục đường tròn và mặt phẳng trung trực để tìm tâm hình cầu ngoại tiếp hình chóp . + Tập hợp các điểm cách đều một điểm cố định một độ dài không đổi. + Trục đường tròn ngoại tiếp của một tam giác . + Mặt phẳng trung trực của một đoạn thẳng . + Diện tích mặt cầu : S = 4 2Rp + Thể tích khối cầu: V = 3 4 R 3 p + Tập hợp các điểm cách đều một điểm cố định một độ dài không đổi. + Trục đường tròn ngoại tiếp của một tam giác . + Mặt phẳng trung trực của một đoạn thẳng . + Diện tích mặt cầu : S = 4 2Rp b) * R = 2 SC = 1 2 2 2 2SA AB BC+ + = 6 2 a * S = 2 264 2 6a ap = æ ö ç ÷ç ÷è ø p ; * V = 3 34 6 3 2 6a ap = æ ö pç ÷ç ÷è ø Bài 4: Cho chóp S.ABC có SA = a, SB = b, SC = c và ba cạnh SA, SB, SC đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó. HD: * Gọi I là trung điểm AB. Kẻ D vuông góc với mp(SAB) tại I * Dựng mp trung trực của SC cắt D tại O Þ OC = OS (1) * I là tâm đường tròn ngoại tiếp D SAB (vì D SAB vuông tại S) ÞOA = OB = OS (2) * Từ (1) và (2) Þ OA = OB = OC = OS Vậy: A, B, C, S thuộc S(O; OA) * R = OA = 2 2 2 2 2 2 SC AB OI AI+ = +æ ö æ öç ÷ ç ÷è ø è ø = 2 2 2 4 a b c+ + * S = 2 2 2 2 2 2 24 4 a b c (a b c ) + +p = p + + æ ö ç ÷ç ÷è ø V= 3 2 2 2 2 2 2 2 2 24 1 3 4 6 a b c (a b c ) a b c + +p = p + + + + æ ö ç ÷ç ÷è ø Bài 5: Cho lăng trụ tam giác đều có đáy là tam giác đều các cạnh đều bằng a, cạnh bên bằng b. Tính thể tích mặt cầu đi qua các đỉnh của lăng trụ HD: -Gọi O và O’ là tâm ∆ABC và ∆A’B’C’ thí OO’ là trục của đường tròn ngoại tiếp ∆ABC và ∆A’B’C’ -Gọi I là trung điểm OO’ thì IA = IB =IC = IA’ = IB’ = IC’ hay I là tâm mặt cầu ngoại tiếp lăng trụ -Bán kính mặt cầu là R = IA Tam giác AOI có: AO = 2 13 a 3 a 32 3 2 3AA = = OI = 1 12 2 b 2OO ' AA '= = c b a I O S C B A 14 + Biết tính thể tích và diện tích hình cầu + Hướng dẫn học sinh tự rèn luyện cũng cố chuẩn kiến thức và các kĩ năng đã được giáo viên hướng dẫn qua các ví dụ trên . + Thể tích khối cầu: V = 3 4 R 3 p + Học sinh tự ôn tập , tự rèn luyện và cũng cố các kiến thức cơ bản thông qua các bài luyện tập .. ⇒AI2=OA2+OI2= 2 2 2a b 7a 3 4 12+ = ⇒ AI = 2 3 a 7 V= 33 3 33 21.aa 7 7 a .28 7 7 a 74 4 3 3 8 3 3 72 3 18 3 54R . p pp = p = = = AI2 = 2 22 2 4a 3b4a 3b 12 2 3AI R ++ =Þ = 3 3 2 23 2 2 2 24 4 1 1 3 3 8.3 3 18 3V R (4a 3b ) .(4a 3b )= p = p + = + LUYỆN TẬP Bài 1: Một hình trụ có bán kính đáy r = 5cm và khoảng cách giữa hai đáy bằng 7cm. a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ b) Tính thể tích của khối trụ c) Cắt khối trụ bởi một mặt phẳng song song với trục và cách trụ 3cm. Hãy tính diện tích của thiết diện được tạo nên Đs: Sxq = 70p (cm2); Stp = 120p (cm2) , V= 175p (cm3) , tdS = 56 (cm2) Bài2: Hình trụ có bán kính r và chiều cao h = r 3 a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ b) Tính thể tích của khối trụ c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 300. Tính khoảng cách giữa đường thẳng AB và trục của hình trụ Đs: Sxq = 2 3 p r2 .; Stp = 2 ( 3 1)+ p r2 ; V 3 3r= p ; O’H = 3 2 r Bài 3: Một hình nón có đường sinh bằng l và thiết diện qua trục là tam giác vuông. a) Tính diện tích xung quanh và diện tích toàn phần của nón b) Tính thể tích của khối nón Đs: Sxq = 2 2 lp ;Stp= 2 1 1 22 læ ö+ pç ÷è ø ; V = 3 6 2 lp= Bài 4: Cho hình nón tròn xoay có đướng cao h = 20cm, bán kính đáy r = 25cm. a) Tính diện tích xung quanh và diện tích toàn phần của hình nón b) Tính thể tích của khối nón c) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12cm. Tính diện tích của thiết diện đó Đs:Sxq= 25p 1025 (cm2) ; Stp= 25p 1025 + 625p V = 2 2 1 25 20 3 . .p (cm3) ; SSAB = 500(cm2) 15 Bài 5: Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân , cạnh huyền bằng 2a a) Tính diện tích xung quanh và diện tích toàn phần của hình nón b) Tính thể tích của khối nón c) Cho dây cung BC của đường tròn đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng chứa đáy hình nón một góc 600. Tính diện tích tam giác SBC Đs : Sxq = 2 2 2 ap ; Stp= 22 1 2 ( ) a+ p ; V = 3 2 12 ap= ; SSBC = 2 2 3 a Bài 6 :Cho hình chóp tứ giác đều S.ABCD có các cạnh bên bằng a và mặt chéo SAC là tam giác đều. a) Tìm tâm và bán kính mặt cầu ngoại tiếp hình chóp. b) Qua A, dựng mặt phẳng ( )a vuông góc với SC. Tính diện tích thiết diện tạo bởi mặt phẳng ( )a và hình chóp Đáp số: a 3R 3 = 2 AMNP a 3 S 6 = Bài 7 : Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, mặt bên hợp với mặt đáy một góc bằng j . Xác định tâm và tính bán kính của mặt cầu ngoại tiếp chóp. Đáp số: 23 (4 tan ) . 12 tan a R j j + = Bài 8 : Cho tứ diện ABCD vớiAB AC a, BC b.= = = Hai mặt phẳng (BCD) và (ABC) vuông góc nhau và có 0BDC 90 .Ð = Xác định tâm và tính bán kính mặt cầu ngoại tiếp tứ diện ABCD theo a và b. Đáp số: 2 2 2 a R 4a b = - Bài 9: Cho hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 30o. Tính thể tích mặt cầu ngoại tiếp hình chóp. Đs : V 38 2 9 3a= Bài 10: Cho mặt cầu đường kính AB=2R. Gọi I là điểm trên AB sao cho AI=h. Một mặt phẳng vuông góc với AB tại I cắt mặt cầu theo đường tròn (C). a) Tính thể tích khối nón đỉnh A và đáy là (C). b)Định vị trí điểm I để thể tích trên đạt giá trị lớn nhất. Đs V= )2( 33 1 22 hrhhr -= pp với 0<h<2R ;Vmax 3 4Rh =Û 16 CÁC BÀI HÌNH HỌC KHÔNG GIAN TRONG ĐỀ THI TỐT NGHIỆP Bài 1 : Cho hình chóp tam giác đều S.ABCcó cạnh đáy bằng a khoảng cách giữa cạnh bên và cạnh đáy đối diện bằng b tính thể tích khối chóp theo a và b. Bài 2 :Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SBD) và mặt phẳng đáy bằng 60 o . Tính thể tích khối chóp S.ABCD theo a. (TN-THPT2010). Bài 3: Cho hình chóp S.ABC có mặt bên SBC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Biết tính thể tích khối chóp S.ABC theo a. (TN-THPT 2009). Bài 4 :Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 2a. Gọi I là trung điểm của cạnh BC. 1) Chứng minh SA vuông góc với BC. 2) Tính thể tích khối chóp S.ABI theo a. (TN-THPT 2008) Bài 5: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại đỉnh B, cạnh bên SA vuông góc với đáy. Biết SA = AB = BC = a. Tính thể tích của khối chóp S.ABC. (TN THPT 2007) Bài 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, cạnh bên SB bằng 1. Tính thể tích của khối chóp S.ABCD. 2. Chứng minh trung điểm của cạnh SC là tâm mặt cầu ngoại tiếp hình chóp S.ABCD. (TN-THPT 2006) Bài 7: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt phẳng (SAB) vuông góc với mặt phẳng đáy,SA=SB, góc giữa đường thẳng SC và mặt phẳng đáy bằng 45o . Tính theo a thể tích của khối chóp S.ABCD. (Khối A-CĐ 2010). Bài 8: Cho hình chóp tứ giác đều S.ABCD có Gọi M,N và P lần lượt là trung điểm của các cạnh SA,SB và CD Chứng minh rằng đường thẳngMN vuông góc với đường thẳng SP. Tính theo a thể tích của khối tứ diện AMNP. (Khối A- CĐ 2009)
Tài liệu đính kèm:
 16.BÁO CÁO ÔN TẬP HÌNH HỌC KHÔNG GIAN-1.pdf
16.BÁO CÁO ÔN TẬP HÌNH HỌC KHÔNG GIAN-1.pdf





