Bài tập trắc nghiệm môn Toán Lớp 12 - Cực trị của hàm số (Có đáp án)
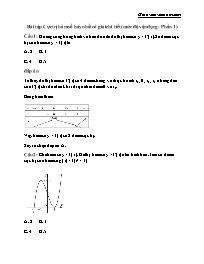
Câu 1: Đường cong trong hình vẽ bên dưới là đồ thị hàm số y = f'(x). Số điểm cực trị của hàm số y = f(x) là:
A. 2 B. 3
C. 4 D. 5
Câu 2: Cho hàm số y = f(x). Đồ thị hàm số y = f'(x) như hình bên. Tìm số điểm cực trị của hàm số g(x) = f(x2 - 3)
Bạn đang xem 20 trang mẫu của tài liệu "Bài tập trắc nghiệm môn Toán Lớp 12 - Cực trị của hàm số (Có đáp án)", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Bài tập Cực trị hàm số hay nhất có giải chi tiết (mức độ vận dụng - Phần 1)
Câu 1: Đường cong trong hình vẽ bên dưới là đồ thị hàm số y = f'(x). Số điểm cực trị của hàm số y = f(x) là:
A. 2 B. 3
C. 4 D. 5
đáp án
Ta thấy đồ thị hàm số f'(x) có 4 điểm chung với trục hoành x1, 0, x2, x3 nhưng dấu của f'(x) chỉ đổi dấu khi x đi qua hai điểm 0 và x3.
Bảng biến thiên:
Vậy hàm số y = f(x) có 2 điểm cực trị.
Suy ra chọn đáp án A.
Câu 2: Cho hàm số y = f(x). Đồ thị hàm số y = f'(x) như hình bên. Tìm số điểm cực trị của hàm số g(x) = f(x2 - 3)
A. 2 B. 3
C. 4 D. 5
đáp án
Ta có g'(x) = 2x. f'(x2 – 3)
Bảng biến thiên:
Dựa vào bảng biến thiên và đối chiếu với các đáp án suy ra ta chọn B.
Chú ý: Dấu của g’(x) được xác định như sau: Ví dụ xét trên khoảng (2; +∞)
• x ∈ (2; +∞) → x > 0 (1)
• x ∈ (2; +∞) ⇒ x2 > 4 ⇒ x2 - 3 > 1 -theo do thi f'(x)→ f'(x2 - 3) (2)
Từ (1) và (2) suy ra g'(x) = 2x.f'(x2 – 3) > 0 trên khoảng (2; +∞) nên g'(x) mang dấu “+”.
Nhận thấy các nghiệm x = 1 hoặc x = -1 và x = 0 là các nghiệm bội lẻ nên g'(x) qua nghiệm đổi dấu; các nghiệm x = 2 hoặc x = -2 là nghiệm bội chẵn (lí do dựa vào đồ thị ta thấy f'(x) tiếp xúc với trục hoành tại điểm có hoành độ bằng 1 nên qua nghiệm không đổi dấu.
Câu 3: Cho hàm số y = f(x) có đạo hàm trên R và có bảng xét dấu của y = f'(x) như sau
Hỏi hàm số g(x) = f(x2 - 2x) có bao nhiêu điểm cực tiểu ?
A. 1 B. 2
C.3 D. 4
đáp án
Ta có g'(x) = (2x - 2). f'(x2 – 2x)
Bảng biến thiên
Dựa vào bảng biến thiên và đối chiếu với các đáp án suy ra ta chọn A.
Câu 4: Cho hàm số y = f(x) có đạo hàm liên tục trên R và f(0) < 0 đồng thời đồ thị hàm số y = f'(x) như hình vẽ bên dưới
Số điểm cực trị của hàm số g(x) = f2(x) là
A. 1 B. 2
C. 3 D. 4
đáp án
Dựa vào đồ thị, ta có:
Bảng biến thiên của hàm số y = f(x)
Bảng biến thiên của hàm số g(x)
Vậy hàm số g(x) có 3 điểm cực trị.
Suy ra chọn đáp án C.
Câu 5: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y = x4 + 2mx2 = 1 có ba điểm cực trị tạo thành một tam giác vuông cân.
đáp án
Tập xác định: D = R.
y' = 4x3 + 4mx; y' = 0 ⇔ 4x3 + 4mx = 0
Hàm số có 3 cực trị khi và chỉ khi phương trình y' = 0 có 3 nghiệm phân biệt nghĩa là phương trình (*) có 2 nghiệm phân biệt khác 0 ⇔ -m > 0 hay m < 0. (loại đáp án C và D)
Vậy tọa độ 3 điểm lần lượt là: A(0; 1), B(-√(-m), 1 - m2), C(√(-m), 1 - m2)
Ta có AB→ = (-√(-m), -m2); AC→ = (√(-m), -m2)
Vì tam giác ABC vuông cân tại A nên :
AB→. AC→ = 0 ⇔ -√(m2) + m2.m2 = 0
⇔ -|m| + m4 = 0 ⇔ m + m4 = 0
Nên m = -1 (vì m < 0)
Vậy với m = -1 thì hàm số có 3 cực trị tạo thành một tam giác vuông cân.
Suy ra chọn đáp án B.
Câu 6: Cho hàm số y = f(x) có đạo hàm trên R. Đồ thị hàm số y = f'(x) như hình vẽ bên dưới
Số điểm cực trị của hàm số g(x) = f(x - 2017) - 2018x + 2019 là
A. 1 B. 2
C. 3 D. 4
đáp án
Ta có: g'(x)= f'(x - 2017) – 2018
Xét phương trình: g'(x) = 0 hay f'(x - 2017) = 2018
Dựa vào đồ thị hàm số y = f'(x) suy ra phương trình f'(x - 2017) = 2018 có 1 nghiệm đơn duy nhất.
Suy ra hàm số g(x) có 1 điểm cực trị.
Suy ra chọn đáp án A.
Câu 7: Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = x4 – 2mx2 có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.
A. m > 0 B. m < 1
C. 0 < m < 3√4 D. 0 < m < 1
đáp án
Ta có: y' = 4x3 – 4mx = 4m(x2 – m) (*)
+ Để đồ thị hàm số đã cho có 3 điểm cực trị khi và chỉ khi phương trình (*) có 3 nghiệm phân biệt ⇔ m > 0 .
+ Xét y' = 0
Các điểm cực trị tạo thành tam giác cân có đáy bằng 2√m, đường cao bằng m2. (như hình minh họa)
Ta được SΔABC = 1/2. AC.BD = √m.m2
Để tam giác có diện tích nhỏ hơn 1 thì: √m.m2 < 1 ⇔ m5 < 1 ⇔ 0 < m < 1
Suy ra chọn đáp án D.
Câu 8: Cho hàm số y = f(x) có đạo hàm trên R. Đồ thị hàm số y = f'(x) như hình vẽ bên dưới. Hỏi hàm số g(x) = f(x) + x đạt cực tiểu tại điểm nào dưới đây ?
A. x = 0 B. x = 1
C. x = 2 D. Không có điểm cực tiểu.
đáp án
+ Ta có đạo hàm: g'(x) = f'(x) + 1
Do đó g'(x)= 0 ⇔ f'(x) = -1
+ Suy ra số nghiệm của phương trình g'(x) = 0 chính là số giao điểm giữa đồ thị của hàm số f'(x) và đường thẳng y = -1.
Dựa vào đồ thị ta suy ra:
Lập bảng biến thiên cho hàm g(x) ta thấy g(x) đạt cực tiểu tại x = 1.
Suy ra chọn đáp án B.
Câu 9: Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = x3 – 3mx2 + 4m3 có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa độ.
đáp án
Đạo hàm y' = 3x2 – 6mx
Đồ thị của hàm số có hai điểm cực trị A(0, 4m3) và B(2m, 0)
SΔABC = 1/2.OA.OB = 4 ⇔ 1/2. |4m3.2m| = 4 ⇔ 4m4 = 4 ⇔ m = 1 hoặc m = -1.
Suy ra chọn đáp án B.
Câu 10: Cho hàm số y = f(x) có đạo hàm trên R. Đồ thị hàm số y = f'(x) như hình vẽ bên dưới.
Hàm số g(x) = f(x) - x3/3 + x2 - x + 2 đạt cực đại tại
A. x = -1 B. x = 0
C. x = 1 D. x = 2
đáp án
Ta có đạo hàm: g'(x) = f'(x) – x2 + 2x - 1
Xét g'(x)= 0 ⇔ f'(x) – x2 + 2x - 1 = 0
⇔ f'(x) = x2 – 2x + 1 = (x - 1)2
Suy ra số nghiệm của phương trình g'(x) = 0 chính là số giao điểm giữa đồ thị của hàm số f'(x) và parapol (P): y = (x - 1)2
Dựa vào đồ thị ta suy ra
Bảng biến thiên
Dựa vào bảng biến thiên ta thấy g(x) đạt cực đại tại x = 1.
Suy ra chọn đáp án C.
Câu 11: Cho hàm số y = f(x) có đạo hàm trên R. Đồ thị hàm số y = f'(x) như hình vẽ bên dưới. Hàm số g(x) = 2f(x) + x2 đạt cực tiểu tại điểm
A. x = -1 B. x = 0
C. x = 1 D. x = 2
đáp án
Ta có g'(x) = 2f'(x) + 2x.
Xét phương trình g'(x)=0 hay f'(x) = - x
Suy ra số nghiệm của phương trình g'(x) = 0 chính là số giao điểm giữa đồ thị của hàm số f'(x) và đường thẳng y = - x
Dựa vào đồ thị ta suy ra
Bảng biến thiên
Dựa vào bảng biến thiên ta thấy g(x) đạt cực tiểu tại x = 0 .
Suy ra chọn đáp án B.
Câu 12: Có tất cả bao nhiêu giá trị nguyên của m để hàm số y = x8 + (m - 2)x5 – (m2 – 4).x4 + 1 đạt cực tiểu tại x = 0?
A. 3 B. 5
C. 4 D. Vô số.
đáp án
Ta xét các trường hợp sau
* Nếu m2 - 4 = 0 ⇒ m = 2 hoặc m = -2
• Khi m= 2 thì y' = 8x7. Suy ra: y' = 0 khi x = 0 là điểm cực tiểu.
• Khi m = - 2 thì y'= x3(8x4 – 20).
Suy ra: y' = 0
Lập bảng biến thiên ta thấy hàm số đạt cực đại tại x = 0 ( loại)
* Nếu m2 - 4 ≠ 0 ⇒ m ≠ 2 hoặc m ≠ -2. Khi đó ta có:
y'= 8x7 + 5(m - 2).x4 – 4(m2 – 4).x3
y' = x2[8x5 + 5(m - 2)x2 - 4(m2 - 4)x]
Số cực trị của hàm y = x8 + (m - 2)x5 - (m2 - 4)x4 + 1 bằng số cực trị của hàm g’(x) với:
Nếu x = 0 là điểm cực tiểu thì g''(0) > 0. Khi đó
-4(m2 - 4) > 0 ⇔ m2 - 4 < 0 ⇒ -2 < m < 2 ⇒ m = {-1; 0; 1}
Vậy có 4 giá trị nguyên của m là {-1; 0; 1; 2}.
Suy ra chọn đáp án C.
Câu 13: Cho hàm số y = f(x) có đạo hàm trên R. Đồ thị hàm số y = f'(x) như hình vẽ bên dưới. Hỏi đồ thị hàm số g(x) = f(x) + 3x có bao nhiểu điểm cực trị ?
A. 2 B. 3
C. 4 D. 7
đáp án
Ta có đạo hàm g'(x)= f'(x) + 3
Xét phương trình g'(x) = 0 hay f'(x)= - 3
Suy ra số nghiệm của phương trình g'(x) = 0 chính là số giao điểm giữa đồ thị của hàm số f'(x) và đường thẳng y = -3.
Dựa vào đồ thị ta suy ra
Ta thấy x = -1, x = 0, x = 1 là các nghiệm đơn và x = 2 là nghiệm kép nên đồ thị hàm số
g(x) = f(x) + 3x có 3 điểm cực trị tại các điểm x = -1, x = 0 và x = 1.
Suy ra chọn đáp án B.
Câu 14: Cho hàm số sau. Tìm giá trị của m để hàm số đã cho đạt cực trị tại x1, x2 và thỏa mãn: x1 + 2x2 = 1.
đáp án
Ta có đạo hàm: y'= mx2 – 2(m - 1)x + 3(m - 2)
Yêu cầu của bài toán tương đương y' = 0 có hai nghiệm phân biệt x1, x2 thỏa mãn: x1 + 2x2 = 1
Câu 15: Cho hàm số bậc bốn y = f(x). Đồ thị hàm số y = f'(x) như hình vẽ bên.
Số điểm cực đại của hàm số là:
A. 1 B. 2
C. 3 D. 4
đáp án
Ta có:
Bảng xét dấu
Từ đó suy ra hàm số có 1 điểm cực đại.
Chú ý: Cách xét dấu “-” hay “+” của g'(x) để cho nhanh nhất ta lấy một giá trị x0 thuộc khoảng đang xét rồi thay vào g'(x).
Chẳng hạn với khoảng (-1; -1 + √2) ta chọn
Vì dựa vào đồ thị ta thấy f'(√2) < 0
Suy ra chọn đáp án A.
Câu 16: Cho hàm số y = f(x). Đồ thị hàm số y = f'(x) như hình vẽ dưới đây
Số điểm cực trị của hàm số g(x) = e2f(x)+1 + 5f(x) là
A. 1 B. 2
C. 3 D. 4
đáp án
+ Ta thấy đồ thị của hàm số f'(x) cắt trục hoành tại 3 điểm phân biệt.
Suy ra hàm số f(x) có 3 điểm cực trị.
+ Ta có: g'(x) = 2f'(x).e2f(x)+1 + f'(x).5f(x).ln5 = f'(x).(2e2f(x)+1 + 5f(x).ln5)
+ Vì 2e2f(x)+1 + 5f(x).ln5 > 0 với mọi x nên g'(x) = 0 ⇔ f'(x) = 0.
Suy ra số điểm cực trị của hàm số g(x) bằng số điểm cực trị của hàm số f(x).
Vậy hàm số g(x) có 3 điểm cực trị.
Suy ra chọn đáp án C.
Câu 17: Cho hàm số y = f(x). Đồ thị hàm số y = f'(x) như hình vẽ bên dưới và f'(x) < 0 với mọi x ∈ (-∞; -3,4) ∪ (9; +∞). Đặt g(x) = f(x) - mx + 5. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) có đúng hai điểm cực trị ?
A. 4 B. 7
C. 8 D. 9
đáp án
Ta có: g'(x) = f'(x) - m.
Xét phương trình: g'(x) = 0 hay f'(x) – m= 0 ⇔ f'(x) = m
Để hàm số g(x) có đúng hai điểm cực trị khi và chỉ khi phương trình g'(x) = 0 có hai nghiệm đơn ( hoặc nghiệm bội lẻ phân biệt)
Suy ra chọn đáp án C.
Câu 18: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x4 – 2mx2 + 1 có ba điểm cực trị A(0,1), B, C thỏa mãn BC = 4?
A. m = 4 hoặc m = -4. B. m = √2.
C. m = 4. D. m = √2 hoặc m = -√2.
đáp án
Cách 1:
+ Ta có: y' = 4x3 - 4mx = 4x(x2 - m);
+ Để hàm số có ba điểm cực trị khi và chỉ khi y' = 0 có ba nghiệm phân biệt ⇔ m > 0
+ Suy ra tọa độ các điểm cực trị của đồ thị hàm số là:
A(0;1), B(√m; 1 - m2) và C(-√m; 1 - m2)
Để BC = 4 ⇔ 2√m = 4 ⇔ √m = 2 ⇔ m = 4 (thỏa mãn).
Cách 2: Áp dụng công thức giải nhanh:
Điều kiện để có ba cực trị là ab 0
Để độ dài BC = m0 khi và chỉ khi:
am02 + 2b = 0 ⇔ 1.42 + 2.(-2m) = 0 ⇔ m = 4
Suy ra chọn đáp án C.
Câu 19: Cho hàm số y = x4 – 2(m + 1)x2 + m2 với m là tham số thực. Tìm tất cả các giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác vuông.
A. m = -1 B. m = 0
C. m = 1 D. m = 2
đáp án
Cách 1.
* Ta có đạo hàm: y'= 4x3 – 4(m + 1)x = 4x(x2 - m - 1)
* Để hàm số có ba điểm cực trị khi và chỉ khi y' = 0 có ba nghiệm phân biệt:
⇔ m + 1 > 0 ⇔ m > -1.
Suy ra tọa độ các điểm cực trị của đồ thị hàm số là:
A(0; m2), B(√(m + 1); -2m - 1) và C(-√(m + 1); -2m - 1)
Khi đó AB− = (√(m + 1); -2m - 1 - m2) và AC− = (-√(m + 1); -2m - 1 - m2)
Để tam giác ABC vuông: AB−.AC− = 0
Cách 2. Áp dụng công thức giải nhanh:
Điều kiện để có ba cực trị ab -1
Để tam giác ABC vuông điều kiện là: 8a + b3 = 0
⇔ 8.1 + [-2(m + 1)]3 = 0 ⇔ m = 0
Suy ra chọn đáp án B.
Câu 20: Tìm giá trị thực của tham số m sao cho đồ thị của hàm số y = x4 + 2mx2 + 1 có ba điểm cực trị tạo thành tam giác vuông cân.
đáp án
Ta có:
* Để hàm số có ba điểm cực trị khi và chỉ khi (*) có hai nghiệm phân biệt khác 0
⇔ -m > 0 hay m < 0
* Khi đó toạ độ ba điểm cực trị của đồ thị hàm số là:
A(0;1), B(√(-m); -m2 + 1), C(-√(-m); -m2 + 1)
Ta có: AB = AC nên tam giác ABC cân tại A nên điều kiện để tam giác ABC vuông cân là:
Suy ra chọn đáp án B.
Câu 21: Cho hàm số y = 3x4 + 2(m - 2018).x2 + 2017 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có một góc bằng 120o.
A. m = - 2018 B. m = -2017
C. m = 2017 D. m = 2018
đáp án
Cách 1.
Ta có: y' = 12x3 + 4(m - 2018)x;
Để hàm số có ba điểm cực trị ⇔ 2018 - m > 0 ⇔ m < 2018.
Khi đó, tọa độ các điểm cực trị của đồ thị hàm số là: A(0; 2017)
Do tam giác ABC cân tại A: AB = AC nên ∠BAC = 120o. Áp dụng định lí cosin trong tam giác ABC ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA = AB2 + AB2 – 2.AB.AB.cos120o
⇔ BC2 = 3AB2
⇔ (m - 2018)3 = -1 ⇔ m = 2017 (thỏa mãn)
Cách 2. Áp dụng công thức giải nhanh:
Điều kiện để có ba cực trị: ab < 0 hay m < 2018
Áp dụng công thức giải nhanh:
(với α = ∠BAC, A là điểm cực trị thuộc Oy)
Ta được:
⇔ 3[2(m - 2018)]3 = -8.3 ⇔ m = 2017 thỏa mãn.
Suy ra chọn đáp án C.
Câu 22: Cho hàm số y = 1/4.x4 - (3m + 1)x2 + 2(m + 1) với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có trọng tâm là gốc tọa độ.
A. m = -2/3. B. m = 2/3.
C. m = -2/3. D. m = 1/3.
đáp án
Cách 1.
Ta có: y' = x3 - 2(3m + 1)x = x[x2 - 2(3m + 1)]
Để hàm số có ba điểm cực trị ⇔ 2(3m + 1) > 0 ⇔ m > -1/3.
Khi đó đồ thị hàm số có ba điểm cực trị là: A(0; 2(m + 1))
Suy ra tọa độ trọng tâm của tam giác ABC là :
Để G ≡ O ⇔ 2(m + 1) + 2(-9m2 - 4m + 1) = 0
Cách 2. Áp dụng công thức giải nhanh:
Điều kiện để có ba cực trị ab -1/3.
Yêu cầu bài toán: G ≡ O ⇔ b2 - 6ac = 0 ⇔ (3m + 1)2 - 6.1/4.2(m + 1) = 0
Suy ra chọn đáp án D.
Câu 23: Cho hàm số y = 9/8.x4 + 3(m - 3)x2 + 4m + 2017 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành tam giác đều.
A. m = -2 B. m = 2
C. m = 3 D. m = 2017
đáp án
Cách 1.
Ta có: y' = 9/2.x3 + 6(m - 3)x;
Để hàm số có ba điểm cực trị khi và chỉ khi (*) có 2 nghiệm phân biệt khác 0.
⇔ 4(m - 3) > 0 ⇔ m < 3
Khi đó tọa độ ba điểm cực trị của đồ thị hàm số là: A(0; 4m + 2017)
Do tam giác ABC cân tại A nên để tam giác ABC đều thì AB = BC hay AB2 = BC2
Cách 2. Áp dụng công thức giải nhanh:
Điều kiện để có ba cực trị ab < 0 hay m < 3
Để tam giác tạo bởi điểm cực trị là tam giác đều khi và chỉ khi:
b3 = -24a hay 27(m - 3)3 = -27 ⇔ m = 2
Suy ra chọn đáp án B.
Câu 24: Cho hàm số y = x4 – mx2 + m - 2 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác có bán kính đường tròn nội tiếp bằng 1
A. m = -2 B. m = 1
C. m = 2 D. m = 4
đáp án
Cách 1.
Ta có: y' = 4x3 - 2mx = 2x(2x2 - m);
Để hàm số có ba điểm cực trị khi và chỉ khi m > 0.
Khi đó tọa độ ba điểm cực trị của đồ thị hàm số là: A(0; m - 2)
Suy ra:
Ta có:
Đặt
Ta được phương trình:
Cách 2. Áp dụng công thức giải nhanh:
Điều kiện để có ba cực trị là ab 0.
Yêu cầu bài toán:
Suy ra chọn đáp án D.
Câu 25: Tìm tất cả các giá trị thực của tham số m để hàm số sau có cực đại và cực tiểu.
A. m < 0 B. m = 0
C. m ∈ R D. m > 0
đáp án
Tập xác định: D = R \ {1}.
Đạo hàm
Đặt g(x) = x2 – 2x – m + 1
Để hàm số có cực đại và cực tiểu khi và chỉ khi g(x) = 0 có hai nghiệm phân biệt khác 1.
Suy ra chọn đáp án D.
Câu 26: Tìm tất cả các giá trị thực của tham số m để hàm số sau đạt cực đại tại x = 2.
A. m = -1 B. m = -3
C. m = 1 D. m = 3
đáp án
TXĐ: D = R \ {-m}.
Đạo hàm
Hàm số đạt cực đại tại x = 2
Thử lại với m = -1 thì hàm số đạt cực tiểu tại x = 2: không thỏa mãn.
Thử lại với m = -3 thì hàm số đạt cực đại tại x = 2: thỏa mãn.
Suy ra chọn đáp án B.
Câu 27: Gọi xCĐ, xCT lần lượt là điểm cực đại, điểm cực tiểu của hàm số y = sin2x- x trên đoạn [0; π]. Mệnh đề nào sau đây là đúng?
A. xCD = π/6; xCT = 5π/6 B. xCD = 5π/6; xCT = π/6
C. xCD = π/6; xCT = π/3 D. xCD = π/3; xCT = 2π/3
đáp án
Ta có y' = 2cos2x - 1 và y'' = -4sin2x.
Xét trên đoạn [0; π], ta có y' = 0
Do đó:
Vậy xCD = π/6; xCT = 5π/6
Suy ra chọn đáp án A.
Câu 28: Tìm giá trị cực đại của hàm số y = x + 2cosx trên khoảng (0;π).
đáp án
Đạo hàm y' = 1 - 2sinx và y'' = -2cosx.
Xét trên khoảng (0;π), ta có
Do đó:
Vậy giá trị cực đại của hàm số là:
Suy ra chọn đáp án C.
Câu 29: Biết rằng trên khoảng (0; 2π) hàm số y = a.sinx + b.cosx + x đạt cực trị tại x = π/3 và x = π. Tính tổng S = a + b
A. S = 3 B. S = √3/3 + 1
C. S = √3 + 1 D. S = √3 - 1
đáp án
Đạo hàm: y' = a.cosx – b.sinx + 1.
Hàm số đạt cực trị tại x = π/3 và x = π
nên
⇒ S = a + b = √3 + 1
Suy ra chọn đáp án C.
Câu 30: Hàm số y = (x2 - 4)2(1 - 2x)3 có bao nhiêu điểm cực trị?
A. 3. B. 4.
C. 5. D. 6.
đáp án
Đạo hàm y' = 2.2x(x2 - 4)(1 - 2x)3 + (x2 - 4)2.3.(-2).(1 - 2x)2
= (1 - 2x)2(x2 - 4).[4x(1 - 2x) - 6(x2 - 4)]
= -2(1 - 2x)2(x2 - 4)(7x2 - 2x - 12)
Phương trình y' = 0 có 4 nghiệm đơn nên hàm số có 4 điểm cực trị.
Suy ra chọn đáp án B.
Tài liệu đính kèm:
 bai_tap_trac_nghiem_mon_toan_lop_12_cuc_tri_cua_ham_so_co_da.docx
bai_tap_trac_nghiem_mon_toan_lop_12_cuc_tri_cua_ham_so_co_da.docx






