Bài tập trắc nghiệm môn Toán Lớp 12 - Chủ đề 2: Tổ hợp. Xác suất. Quy tắc đếm (Có đáp án)
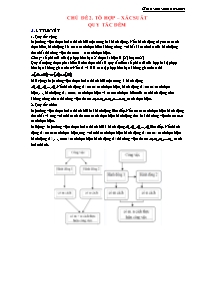
Câu 4. Trong kì thi tuyển nhân viên chuyên môn cho công ty cổ phần Giáo dục trực tuyến VEDU, ở khối A có thí sinh đạt điểm giỏi môn Toán, thí sinh đạt điểm giỏi môn Vật lí, thí sinh đạt điểm giỏi môn Hóa học, thí sinh đạt điểm giỏi cả hai môn Toán và Vật lí, thí sinh đạt điểm giỏi cả hai môn Vật lí và Hóa học, thí sinh đạt điểm giỏi cả hai môn Toán và Hóa học, thí sinh đạt điểm giỏi cả ba môn Toán, Vật lí và Hóa học. Có thí sinh mà cả ba môn đều không có điểm giỏi. Hỏi có bao nhiêu thí sinh tham dự tuyển nhân viên chuyên môn cho công ty?
A. . B. . C. . D. .
Câu 5. Người ta phỏng vấn người về ba bộ phim đang chiếu thì thu được kết quả như sau:
Bộ phim A: có người đã xem.
Bộ phim B: có người đã xem.
Bộ phim B: có người đã xem.
Có người đã xem hai bộ phim A và B
Có người đã xem hai bộ phim B và C
Có người đã xem hai bộ phim A và C
Có người đã xem cả ba bộ phim A, B và C.
Số người không xem bất cứ phim nào trong cả ba bộ phim là:
A. . B. . C. . D. .
CHỦ ĐỀ 2. TỔ HỢP – XÁC SUẤT QUY TẮC ĐẾM A. LÝ THUYẾT 1. Quy tắc cộng Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiên, hành động kia có n cách thực hiên không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m + n cách thực hiện. Chú ý: số phần tử của tập hợp hữu hạn X được kí hiệu là |X| hoặc n(X) Quy tắc cộng được phát biểu ở trên thực chất là quy tắc đếm số phần tử của hợp hai tập hợp hữu hạn không giao nhau: Nếu A và B là các tập hợp hữu hạn không giao nhau thì Mở rộng: Một công việc được hoàn thành bởi một trong k hành động .Nếu hành động A1 có m1cách thực hiện, hành động A2 có m2 cách thực hiện,, hành động Ak có mk cách thực hiện và các cách thực hiên của các hành động trên không trùng nhau thì công việc đó có cách thực hiện. 2. Quy tắc nhân Một công việc được hoàn thành bởi hai hành động liên tiếp.Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì công việc đó có m.n cách thực hiện. Mở rộng: Một công việc được hoàn thành bởi k hành độngliên tiếp. Nếu hành động A1 có m1cách thực hiện, ứng với mỗi cách thực hiện hành động A1 có m2 cách thực hiện hành động A2,, có mk cách thực hiện hành động Ak thì công việc đó có cách hoàn thành. HOÁN VỊ- CHỈNH HỢP- TỔ HỢP 1. Hoán vị Cho tập hợp A có n phần tử . Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó. Số các hoán vị của tập hợp có n phần tử được kí hiệu là Pn Định lí 1: với Pn là số các hoán vị chứng minh Việc sắp xếp thứ tự n phần tử của tập hợp A là một công việc gồm n công đoạn. Công đoạn 1: Chọn phần tử xếp vào vị trí thứ nhất: n cách Công đoạn 2: chọn phần tử xếp vào vị trí thứ hai: (n-1) cách Công đoạn thứ i: chọn phần tử xếp vào vị trí thứ i có cách. . Công đoạn thứ n: chọn phần tử xếp vào vị trí thứ n có 1 cách. Theo quy tắc nhân thì có cách sắp xếp thứ tự n phần tử của tập A, tức là có hoán vị. STUDY TIP Hai hoán vị của n phần tử chỉ khác nhau ở thứ tự sắp xếp. Chẳng hạn, hai hoán vị abc và acb của ba phần tử a, b, c là khác nhau. 2. Chỉnh hợp Cho tập A gồm n phần tử . Kết quả của việc lấy k phần tử khác nhau tử n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chinht hợp chập k của n phần tử đã cho. STUDY TIP: Từ định nghĩa ta thấy một hoán vị của tập hợp A có n phần tử là một chỉnh hợp chập n của A. Định lý 2: với là số các chỉnh hợp chập k của n phần tử . Chứng minh Việc thiết lập một chỉnh hợp chập k của tập A có n phần tử là một công việc gồm k công đoạn. Công đoạn 1: Chọn phần tử xếp vào vị trí thứ nhất có n cách thực hiện. Công đoạn 2: Chọn phần tử xếp vào vị trí thứ hai có cách thực hiện. . Sau khi thực hiện xong công đoạn (chọn phần tử của A vào các vị trí thứ 1, 2,., ), công đoạn thứ i tiếp theo là chọn phần tử xếp vào vị trí thứ i có cách thực hiện. Công đoạn cuối, công đoạn k có cách thực hiện. Thoe quy tắc nhân thì có chỉnh hợp chập k của tập A có n phần tử. 3. Tổ hợp Giả sử tập A có n phần tử . Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho. Số các tổ hợp chập k của tập hợp có n phần tử có kí hiệu là . STUDY TIP Số k trong định nghĩa cần thỏa mãn điều kiện . Tuy vậy, tập hợp không có phần tử nào là tập rỗng nên ta quy ước gọi tổ hợp chập 0 của n phần tử là tập rỗng. QUY ƯỚC Định lý 3 Chứng minh Ta có mỗi hoán vị của một tổ hợp chập k của A cho ta một chỉnh hợp chập k của A. Vậy . Định lý 4 (hai tính chất cơ bản của số ) a. Cho số nguyên dương n và số nguyên k với . Khi đó . b. Hằng đẳng thức Pascal Cho số nguyên dương n và số nguyên dương k với . Khi đó . Đọc thêm Trên máy tính cầm tay có chức năng tính tổ hợp, chỉnh hợp như sau: Với tổ hợp ta nhấn tổ hợp phím Ví dụ ta muốn tính ta ấn Với chỉnh hợp ta ấn tổ hợp phím Ví dụ ta muốn tính ta ấn tổ hợp phím B. CÁC DẠNG TOÁN VỀ PHÉP ĐẾM Phương pháp chung: Để đếm số cách lựa chọn để thực hiện một công việc bằng quy tắc cộng, ta thực hiện các bước: Bước 1: Phân tích xem có bao nhiêu phương án riêng biệt để thực hiện công việc (có nghĩa công việc có thể hoàn thành bằng một trong các phương án ). Bước 2: Đếm số cách chọn trong các phương án Bước 3: Dùng quy tắc cộng ta tính được số cách lựa chọn để thực hiện công việc là Để đếm số cách lựa chọn để thực hiện công việc bằng quy tắc nhân, ta thực hiện các bước: Bước 1: Phân tích xem có bao nhiêu công đoạn liên tiếp cần phải tiến hành để thực hiện công việc (giả sử chỉ hoàn thành sau khi tất cả các công đoạn hoàn thành). Bước 2: Đếm số cách chọn trong các công đoạn Bước 3: Dùng quy tắc nhân ta tính được số cách lựa chọn để thực hiện công việc là Một lớp học có 25 học sinh nam và 20 học sinh nữ. Giáo viên chủ nhiệm muốn chọn ra: a) một học sinh đi dự trại hè của trường. b) một học sinh nam và một học sinh nữ dự trại hè của trường. Số cách Chonju trong mỗi trường hợp a và b lần lượt là A. 45 và 500. B. 500 và 45. C. 25 và 500. D. 500 và 25. Lời giải Chọn A a) Bước 1: Với bài toán a thì ta thấy cô giáo có thể có hai phương án để chọn học sinh đi thi: Bước 2: Đếm số cách chọn. Phương án 1: chọn 1 học sinh đi dự trại hè của trường thì có 25 cách chọn. Phương án 2: chọn học sinh nữ đi dự trại hè của trường thì có 20 cách chọn. Bước 3: Áp dụng quy tắc cộng. Vậy có cách chọn. b) Bước 1: Với bài toán b thì ta thấy công việc là chọn học sinh nam và một học sinh nữ. Do vậy ta có 2 công đoạn. Bước 2: Đếm số cách chọn trong các công đoạn. Công đoạn 1: Chọn 1 học sinh nam trong số 25 học sinh nam thì có 25 cách chọn. Công đoạn 2: Chọn 1 học sinh nữ trong số 20 học sinh nữ thì có 20 cách chọn. Bước 3: Áp dụng quy tắc nhân. Vậy ta có cách chọn. STUDY TIP Bài toán ở ví dụ 1 giúp ta cũng cố và định hình các bước giải quyết bài toán đếm sử dụng quy tắc cộng; quy tắc nhân. Chú ý: Quy tắc cộng: Áp dụng khi công việc có nhiều phương án giải quyết. Quy tắc nhân: Áp dụng khi công việc có nhiều công đoạn. Trên giá sách có 10 quyển sách Văn khác nhau, 8 quyển sách Toán khác nhau và 6 quyển sách Tiếng Anh khác nhau. Hỏi có bao nhiêu cách chọn hai quyển sách khác môn nhau? A. 80. B. 60. C. 48. D. 188. Lời giải Chọn D Theo quy tắc nhân ta có: cách chọn một quyển sách Văn và một quyển sách Toán khác nhau. cách chọn một quyển sách Văn và một quyển sách Tiếng Anh khác nhau. cách chọn một quyển sách Toán và một quyển sách Tiếng Anh khác nhau. Theo quy tắc cộng ta có số cách chọn 2 quyển sách khác môn là cách. STUDY TIP Ta thấy bài toán ở ví dụ 2 là sự kết hợp của cả quy tắc cộng và quy tắc nhân khi bài toán vừa cần chia trường hợp vừa cần lựa chọn theo bước. Biển đăng kí xe ô tô có 6 chữ số và hai chữ cái trong số 26 chữ cái (không dùng các chữ và Chữ đầu tiên khác 0. Hỏi số ô tô được đăng kí nhiều nhất có thể là bao nhiêu? A. B. C. 33384960. D. Lời giải Chọn A Theo quy tắc nhân ta thực hiện từng bước. Chữ cái đầu tiên có 24 cách chọn. Chữ cái tiếp theo cũng có 24 cách chọn. Chữ số đầu tiên có 9 cách chọn. Chữ số thứ hai có 10 cách chọn. Chữ số thứ ba có 10 cách chọn. Chữ số thứ tư có 10 cách chọn. Chữ số thứ năm có 10 cách chọn. Chữ số thứ sau có 10 cách chọn. Vậy theo quy tắc nhân ta có là số ô tô nhiều nhất có thể đăng kí. STUDY TIP Có thể phân biệt bài toán sử dụng quy tắc cộng hay quy tắc nhân là phân biệt xem công việc cần làm có thể chia trường hợp hay phải làm theo từng bước. Có bao nhiêu cách xếp 7 học sinh vào một hàng ghế dài gồm 7 ghế sao cho hai bạn và ngồi ở hai ghế đầu? A. cách. B. cách. C. cách. D. cách. Lời giải Chọn C Ta thấy ở đây bài toán xuất hiện hai đối tượng. Đối tượng 1: Hai bạn và (hai đối tượng này có tính chất riêng). Đối tượng 2: Các bạn còn lại có thể thay đổi vị trí cho nhau. Bước 1: Ta sử dụng tính chất riêng của hai bạn và trước. Hai bạn này chỉ ngồi đầu và ngồi cuối, hoán đổi cho nhau nên có cách xếp. Bước 2: Xếp vị trí cho các bạn còn lại, ta có cách xếp. Vậy ta có cách xếp. STUDY TIP Để nhận dạng một bài toán đếm có sử dụng hoán vị của phần tử, ta dựa trên dấu hiệu a. Tất cả phần tử đều có mặt. b. Mỗi phần tử chỉ xuất hiện 1 lần. c. Có sự phân biệt thứ tự giữa các phần tử. d. Số cách xếp phần tử là số hoán vị của phần tử đó Một nhóm 9 người gồm ba đàn ông, bốn phụ nữ và hai đứa trẻ đi xem phim. Hỏi có bao nhiêu cách xếp họ ngồi trên một hàng ghế sao cho mỗi đứa trẻ ngồi giữa hai phụ nữ và không có hai người đàn ông nào ngồi cạnh nhau? A. B. C. D. Lời giải Chọn B Kí hiệu là ghế đàn ông ngồi, là ghế cho phụ nữ ngồi, là ghế cho trẻ con ngồi. Ta có các phương án sau: PA1: PA2: PA3: Xét phương án 1: Ba vị trí ghế cho đàn ông có cách. Bốn vị trí ghế cho phụ nữ có thể có cách. Hai vị trí ghế trẻ con ngồi có thể có cách. Theo quy tắc nhân thì ta có cách. Lập luận tương tự cho phương án 2 và phương án 3. Theo quy tắc cộng thì ta có cách. STUDY TIP Với các bài toán gồm có ít phần tử và vừa cần chia trường hợp vừa thực hiện theo bước thì ta cần chia rõ trường hợp trước, lần lượt thực hiện từng trường hợp (sử dụng quy tắc nhân từng bước) sau đó mới áp dụng quy tắc cộng để cộng số cách trong các trường hợp với nhau. Một chồng sách gồm 4 quyển sách Toán, 3 quyển sách Vật lý, 5 quyển sách Hóa học. Hỏi có bao nhiêu cách xếp các quyển sách trên thành một hàng ngang sao cho 4 quyển sách Toán đứng cạnh nhau, 3 quyển Vật lý đứng cạnh nhau? A. cách. B. cách. C. cách. D. cách. Lời giải Chọn C. Bước 1: Do đề bài cho 4 quyển sách Toán đứng cạnh nhau nên ta sẽ coi như “buộc” các quyển sách Toán lại với nhau thì số cách xếp cho “buộc” Toán này là cách. Bước 2: Tương tự ta cũng “buộc” 3 quyển sách Lý lại với nhau, thì số cách xếp cho “buộc” Lý này là cách. Bước 3: Lúc này ta sẽ đi xếp vị trí cho 7 phần tử trong đó có: + 1 “buộc” Toán. + 1 “buộc” Lý. + 5 quyển Hóa. Thì sẽ có cách xếp. Vậy theo quy tắc nhân ta có cách xếp. STUDY TIP Với các dạng bài tập yêu cầu xếp hai hoặc nhiều phần tử đứng cạnh nhau thì ta sẽ “buộc” các phần tử này một nhóm và coi như 1 phần tử. Một câu lạc bộ phụ nữ của phường Khương Mai có 39 hội viên. Phường Khương Mai có tổ chức một hội thảo cần chọn ra 9 người xếp vào 9 vị trí lễ tân khác nhau ở cổng chào, 12 người vào 12 vị trí khác nhau ở ghế khách mới. Hỏi có bao nhiêu cách chọn các hội viên để đi tham gia các vị trí trong hội thao theo quy định? A. B. C. D. Phân tích Bài toán sử dụng quy tắc nhân khi ta phải thực hiện hai bước: Bước 1: Chọn 9 người vào vị trí lễ tân. Bước 2: Chọn 12 người vào vị trí khách mời. Dấu hiệu nhận biết sử dụng chỉnh hợp ở phần STUDY TIP. Lời giải Chọn D. Bước 1: Chọn người vào vị trí lễ tân. Do ở đây được sắp theo thứ tự nên ta sẽ sử dụng chỉnh hợp. Số cách chọn ra 9 người vào vị trí lễ tân là cách. Bước 2: Chọn người vào vị trí khách mời. Số cách chọn là 12 thành viên trong số các thành viên còn lại để xếp vào khách mời là cách. Vậy theo quy tắc nhân thì số cách chọn các hội viên để đi dự hội thảo theo đúng quy định là cách. STUDY TIP Để nhận dạng một bài toán đếm có sử dụng chỉnh hợp chập của phần tử, ta cần có các dấu hiệu: a. Phải chọn phần tử từ p ... hiện là ” . Có thể thấy rằng các biến cố này đôi một xung khắc. Do viên xúc sắc là cần đối nên xác suất chia đều ra cho 6 mặt, mỗi mặt có xác suất là . Ta có Đáp án B. Gọi là biến cố “học sinh chọn được tăng điểm”. Gọi là biến cố “học sinh chọn học giỏi ngoại ngữ”. Gọi là biến cố “học sinh chọn học giỏi tin học”. Thì và là biến cố “học sinh chọn học giỏi cả ngoại ngữ lẫn tin học”. Ta có Đáp án C. Gọi là biến cố “lấy được ít nhất 2 bóng tốt”. Không gian mẫu: lấy ngẫu nhiên 3 quả bóng thì số cách lấy là TH1: Lấy 3 bóng trong đó có 2 bóng tốt và 1 bóng xấu thì số cách chọn là cách TH2: Lấy 3 bóng đều tốt thì số cách lấy là cách Suy ra . Vậy Đáp án A. Số cách chọn 5 viên bi từ 14 viên bi là . Gọi là biến cố “Trong 5 viên bi được chọn có cả bi xanh và bi trắng” Trong đó: Số cách chọn 5 viên bi toàn bi xanh là cách. Số cách chọn 5 viên bi toàn bi trắng là cách. Suy ra Đáp án A. Gọi là tập hợp những em học khá môn Toán, là tập hợp những em học khá môn Văn. Tập hợp những em học khá cả Toán và Văn là học sinh. Gọi là biến cố “chọn được 3 em học khá môn Toán nhưng không khá môn Văn”. Ta có Số học sinh học khá môn Toán nhưng không khá môn Văn là . cách. . Đáp án B. Con xúc xắc thứ nhất có thể xảy ra 6 kết quả, con thứ hai cũng vậy nên tổng số kết quả có thể xảy ra là Gọi là biến cố “Tổng hai mặt xuất hiện mặt bằng 7”. Dùng phương pháp liệt kê . Đáp án C. Gọi là tập hợp các học sinh giỏi Toán, là tập hợp các học sinh giỏi Văn. là tập hợp các học sinh giỏi cả 2 môn và là tập hợp những học sinh giỏi một trong hai môn (tập hợp các học sinh giỏi). Theo quy tắc cộng tổng quát ta có Gọi là biến cố “chọn được 2 em là học sinh giỏi” và . Đáp án D. Đặt 19 là một số . Ta có số các số có các chữ số khác nhau tạo thành từ với là chữ số đứng đầu là (số) Đáp án D. Số các số có 5 chữ số khác nhau lập được từ tập là (số) Gọi số cần tìm là ta có hoặc (do số đó phải chia hết cho ). Khi đó ta có các trường hợp: , chọn vị trí cho số có cách chọn, ngoài ra trong số còn có hoán vị trong đó. Cuối cùng ta chọn số còn lại có cách chọn. Vậy số các số thuộc trường hợp này có số. , các số thuộc có số thỏa (do nên chỉ có cách chọn ) , các số thuộc có số thỏa mãn. Số các số thỏa mãn yêu cầu là số. Vậy xác suất cần tìm là . Đáp án A. Gọi là biến cố “Chọn em có ít nhất một nam và một nữ”. Số cách chọn bạn bất kì vào ban cán sự lớp là cách. Số cách chọn bạn nam vào ban cán sự lớp là cách. Số cách chọn bạn nữ vào ban cán sự lớp là cách. Vậy số cách chọn ban cán sự lớp có cả nam lẫn nữ là Vậy xác suấtcần tìm là . Đáp án A. Số cách chọn ra học sinh mà không có điều kiện gì là cách Ta sẽ loại trừ các trường hợp có cặp anh em sinh đôi. Đầu tiên ta chọn cặp sinh đôi có cách chọn. Sau đó chọn học sinh còn lại từ học sinh, có cách chọn. Vậy số cách chọn em học sinh thỏa yêu cầu đề bài là: Vậy xác suất cần tìm là . Đáp án A. Số cách xếp người vào bàn là (do ở đây là hoán vị vòng quanh). Gộp các thành viên cùng quốc tịch vào cùng nhóm, trước tiên ta tính số cách xếp mọi người trong các nhóm đó. Theo nguyên tắc “buộc” các phần tử, ta buộc thành các phần tử lớn là Mỹ, Nga, Anh, Pháp. Lúc này bài toán trở thành xếp bốn phần tử vào bốn ghế trên bàn tròn. Cố định nhóm Mỹ, có cách xếp chỗ cho nhóm Nga, cách xếp chỗ cho nhóm Anh, cách xếp chỗ cho nhóm Pháp. Vậy có cách xếp. Vậy xác suất để xếp cho các vị cùng quốc tịch ngồi cạnh nhau là . Đáp án B. Vì đồng xu là cân đối nên xác suất sấp – ngửa của mỗi lần tung là như nhau và bằng . Xác suất để lần tung đồng xu đều sấp là Đáp án C. Gọi là biến cố “Xạ thủ thứ bắn trúng”. Với . ; Gọi là biến cố “Có ít nhất một xạ thủ bắn trúng” thì Đáp án D. Gọi là biến cố “Ném được vòng vào cổ chai”, là biến cố “Ném được vòng vào cổ chai lần đầu”, là biến cố “Ném được vòng vào cổ chai lần thứ 2”, là biến cố “Ném được vòng vào cổ chai lần thứ ba”. ; Đáp án C. Mỗi đồng xu có hai khả năng: ngửa hoặc sấp. Do đó số phần tử của không gian mẫu khi gieo ba đồng xu là . Ta có biến cố đối của là : “Không có đồng xu nào xuất hiện mặt ngửa” “Cả ba đồng xu đều xuất hiện mặt sấp”. Khi đó . Đáp án D. Nhận xét: Do con xúc xắc chỉ có mặt và để ý rằng là giá trị tối đa của tổng Và không lớn hơn là bao nhiêu nên ta sẽ sử dụng phương pháp tính phần bù. Số các bộ thứ tự với là số tự nhiên lớn hơn hoặc bằng và nhỏ hơn hoặc bằng là Xét các bộ thứ tự có tổng . Ta có: Như vậy có tổng cộng bộ thỏa mãn . Số bộ thỏa mãn là Xác suất cần tính là . Đáp án A. Nhận xét: Do con xúc xắc chỉ có mặt và để ý rằng là giá trị tối đa của tổng Và không lớn hơn là bao nhiêu nên ta sẽ sử dụng phương pháp tính phần bù. Số các bộ thứ tự với là số tự nhiên lớn hơn hoặc bằng và nhỏ hơn hoặc bằng là Xét các bộ thứ tự có tổng . Ta có: Như vậy có tổng cộng bộ thỏa mãn . Số bộ thỏa mãn là Xác suất cần tính là . Đáp án B. Vì hai con xúc xắc có cùng mặt nên số phần tử của không gian mẫu là Gọi là số chấm xuất hiện lần lượt trên mặt xanh và mặt đỏ. Khi đó . Đáp án A. Số cách chọn tấm bìa trong tấm bìa và xếp thành một hang ngang là Số cách xếp tấm bìa để không có được số có ba chữ số tức là vị trí đầu tiên là chữ số là Số cách xếp tấm bìa để tạo được số có ba chữ số là Vậy xác suất cần tìm là . Đáp án D. Ta có điều kiện chủ chốt “tích hai số được chọn là một số chẵn” Tồn tại Doít nhất một trong hai số được chọn là chẵn. Gọi là số tự nhiên có hai chữ số khác nhau được lập từ các số đã cho Số cách chọn cách; Số cách chọn cách Số các số có hai chữ số khác nhau tạo được là số có phần tử. Số cách lấy ngẫu nhiên số từ tập : cách Gọi biến cố : “Tích hai số được chọn là một số chẵn” Gọi biến cố : “Tích hai số được chọn là một số lẻ” Số các số lẻ trong : ( cách chọn chữ số hàng đơn vị là lẻ, cách chọn chữ số hang chục khác ). Số cách lấy ngẫu nhiên số lẻ trong số lẻ: cách . Vậy Đáp án D. Chọn ba quả cân có cách. Chọn ba quả cân có tổng trọng lượng nhỏ hơn hoặc bằng có các trường hợp sau: TH1: Trong các quả được lấy ra không có quả cân trọng lượng kg. Ta có là tổng trọng lượng nhỏ nhất có thể. Do đó trong trường hợp này có đúng cách chọn. TH2: Trong các quả được lấy ra có quả cân trọng lượng kg. Khi đó ta có: Trường hợp này ta có cách chọn. Vậy số cách chọn thỏa mãn ycbt là . Xác suất cần tính là: . Đáp án B. Số cách lấy ra tùy ý viên bi trong viên bi đã cho là: Để chọn ra không quá viên bi đỏ từ viên lấy ra là: Lấy ra được viên bi đỏ, viên bi xanh: cách. Lấy ra được viên bi đỏ, viên bi xanh: cách. Lấy ra được viên bi đỏ, viên bi xanh: cách. Vậy xác suất để viên bi chọn ra không quá viên bi đỏ là . Đáp án D. Gọi biến cố : “Lấy tấm thẻ mang số lẻ, tấm thẻ mang số chẵn, trong đó chỉ có đúng tấm thẻ mang số chia hết cho ” Số cách lấy ngẫu nhiên tấm thẻ trong tấm thẻ : cách Trong tấm thẻ có tấm thẻ mang số lẻ, tấm thẻ mang số chẵn, tấm thẻ mang số chia hết cho (chú ý là các thẻ chia hết cho đều là số chẵn) Số cách chọn tấm thẻ mang số lẻ: cách. Số cách chọn tấm thẻ mang số chia hết cho cách Số cách chọn tấm thẻ mang số chẵn không chia hết cho cách Số cách lấy tấm thẻ mang số lẻ, tấm thẻ mang số chẵn trong đó chỉ có đúng tấm thẻ chia hết cho : cách. Vậy Đáp án A. Trong thẻ đã cho có hai thẻ ghi số chia hết cho (các thẻ ghi số và ), thẻ còn lại có ghi số không chia hết cho . Giả sử rút , số cách chọn từ thẻ trong hộp là , số phần tử của không gian mẫu là Gọi là biến cố “Trong số thẻ rút ra có ít nhất một thẻ ghi số chia hết cho ” Số cách chọn tương ứng với biến cố là Ta có Do đó Vậy giá trị nhỏ nhất của là . Vậy số thẻ ít nhất phải rút là. Đáp án A. Phân tích: Cần nhớ lại kiến thức cơ bản về bất đẳng thức tam giác. Ba đoạn thẳng với chiều dài có thể là cạch của một tam giác khi và chỉ khi Lời giải: Số phần tử của không gian mẫu là: Gọi là biến cố “lấy ba đoạn thẳng lấy ra lập thành một tam giác” Các khả năng chọn được ba đoạn thẳng lập thành một tam giác là Số trường hợp thuận lợi của biến cố là . Suy ra xác suất của biến cố là . Đáp án C. Gọi là biến cố “ và có giải thưởng giống nhau”. Vì mỗi học sinh nhận được cuốn sách các loại, nên giả sử có học sinh nhận sách (Lí và Hóa) và học sinh nhận sách (Toán và Hóa). Số phần tử của không gian mẫu là TH1: và nhận sách (Toán, Lí), số khả năng là TH2: và nhận sách (Toán, Hóa), số khả năng là TH1: và nhận sách (Lí, Hóa), số khả năng là Đáp án B. Theo công thức hoán vị vòng quanh ta có: Để xếp các bạn nữ không ngồi cạnh nhau, trước hết ta xếp các bạn nam vào bàn tròn: có cách, giữa bạn nam đó ta sẽ có được ngăn (do ở đây là bàn tròn). Xếp chỉnh hợp bạn nữ vào ngăn đó có cách. Vậy xác suất xảy ra là:. Đáp án C. Phân tích: Đề bài cho các điều kiện khá dài dòng, ta cần đưa chúng về dạng ngắn gọn dễ hiểu hơn. +) “Biết rằng giới chuyên môn đánh giá Phong và Đạt ngang tài ngang sức”: xác suất để Phong và Đạt thắng trong một ván là như nhau và bằng . +) “Khi Đạt thắng được ván và Phong thắng được ván rồi”: nghĩa là Đạt chỉ cần thắng một ván nữa là được ván, còn Phong phải thắng ván nữa mới đạt được. Lời giải: Để xác định xác suất thắng chung cuộc của Đạt và Phong ta tiếp tục chơi thêm các ván “giả tưởng”. Để Phong có thể thắng chung cuộc thì anh phải thắng Đạt ván liên tiếp (vì Đạt chỉ còn một ván nữa là thắng). Như vậy xác suất thắng cuộc của Phong là: Xác suất thắng cuộc của Đạt là Đ Tỉ lệ chia tiền phù hợp là Đáp án D. Phân tích: Bài này điểm mấu chốt là phải liệt kê được các trường hợp mà An thắng Bình ching cuộc. Ví dụ như: Séc : An thắng; Séc : An thắng; Séc : Bình thắng; Séc : An thắng. An thắng chung cuộc. Lưu ý là ta phải tính cả thứ tự các séc An thắng hoặc thua. Như ở ví dụ trên là An thua ở séc thứ. Lời giải: Giả sử số séc trong trân đấu giữa An và Bình là . Dễ dàng nhận thấy . Ta xét các trường hợp: TH1: Trận đấu có séc An thắng cả séc. Xác suất thắng trong trường hợp này là: TH2: Trận đấu có séc An thua trong séc: hoặc và thắng séc thứ . Số cách chọn séc để An thua là: (Chú ý xác xuất để An thua trong séc là ) TH3: Trận đấu có séc An thua 2 séc và thắng ở séc thứ . Số cách chọn trong séc đầu để An thua là cách. Như vậy xác suất để An thắng chung cuộc là: Nhận xét: Trong bài này các bạn rất dễ mắc sai lầm sau: ở trường hợp lại tính số cách chọn ván An thua là mà không để ý rằng séc thứ chắc chắn phải là An thắng. Đáp án D. Phân tích: Với một bài yêu cầu tìm giá trị lớn nhất như thế này thì cách mà ta nghĩ đến đầu tiên là đặt ẩn (là số điểm) rồi sau đó tính biểu thức cần tính (xác suất đạt được số điểm) rồi sau đó tính biểu thức cần tính (xác suất đạt được số điểm) theo ẩn đó, việc còn lại là xử lí biểu thức. Lời giải: Gọi là số điểm bạn đó đạt được ()( ) Bạn đó trả lời đúng câu và trả lời sai câu. +) Xác suất mỗi câu bạn đó đúng là: ; sai là . +) Có cách chọn ra câu đúng. Do đó xác suất được điểm là: Do là lớn nhất nên . Mà nên Nên xác suất bạ đó đạt điểm là lớn nhất. Đáp án C. Ta có Với bộ có cách xáo trộn điểm các lần bắn Với bộ có cách xáo trộn điểm các lần bắn Với bộ có cách xáo trộn điểm các lần bắn. Do đó xác suất để sau lần bắn xạ thủ được đúng điểm là:
Tài liệu đính kèm:
 bai_tap_trac_nghiem_mon_toan_lop_12_chu_de_2_to_hop_xac_suat.docx
bai_tap_trac_nghiem_mon_toan_lop_12_chu_de_2_to_hop_xac_suat.docx






