Tài liệu ôn thi tốt nghiệp THPT môn Toán – Ban Cơ bản
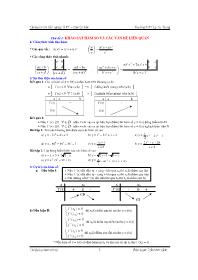
+ Nếu f ’(x) đổi dấu từ + sang - khi qua x0 thì x0 là điểm cực đại
+ Nếu f ’(x) đổi dấu từ - sang + khi qua x0 thì x0 là điểm cực tiểu
+ Nói chung nếu f ’(x) đổi dấu khi qua x0 thì x0 là điểm cực trị
Bạn đang xem 20 trang mẫu của tài liệu "Tài liệu ôn thi tốt nghiệp THPT môn Toán – Ban Cơ bản", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Taøi lieäu oân thi toát nghieäp THPT – Ban Cô baûn Tröôøng THPT Lyù Töï Troïng
Taøi lieäu löu haønh noäi boä Bieân soaïn: Traàn Minh caûnh
1
Chủ ñề 1: KHẢO SÁT HÀM SỐ VÀ CÁC VẤN ðỀ LIÊN QUAN
1/ Công thức tính ñạo hàm:
* Các quy tắc: (u.v)’ = u’.v + u.v’
2
'
'.'.
v
vuvu
v
u −
=
* Các công thức tính nhanh:
( )
'
2
a b
c dax b
cx d cx d
+
= + +
=
2)( dcx
bcad
+
−
,
2
2
'2
)''(
''
'.2'.
'' cxb
c
c
b
b
xcaxba
cxb
cbxax
+
++
=
+
++
2/ Sự ñơn ñiệu của hàm số:
Kết quả 1: Giả sử hàm số y = f(x) có ñạo hàm trên khoảng (a;b)
+ [ f’(x) > 0 ∀∈ (a;b) ] ⇒ [ f ñồng biến (tăng) trên (a;b) ]
+ [ f’(x) < 0 ∀∈ (a;b) ] ⇒ [ f nghịch biến (giảm) trên (a;b) ]
x a b
f’(x) –
f(x)
Kết quả 2:
+ Nếu f ’(x) ≥ 0, D∈∀ , (dấu = chỉ xảy ra tại hữu hạn ñiểm) thì hàm số y = f(x) ñồng biến trên D
+ Nếu f ’(x) ≤ 0, D∈∀ , (dấu = chỉ xảy ra tại hữu hạn ñiểm) thì hàm số y = f(x) nghịch biến trên D
Bài tập 1: Tìm các khoảng ñơn ñiệu của các hàm số sau:
a) y = - 2x2 + 4x + 5 b) y = x3 – 2x2 + x – 2 c) y = 12
4
1 24
−− xx
d) y = - 6x4 + 8x3 – 3x2 – 1 e) y =
5
12
+
−
x
x
f) y =
2
262 2
+
++
x
xx
Bài tập 2: Lập bảng biến thiên của các hàm số sau:
a) y = x + 3 + x−22 b) y = xx −−− 312
c) y = e-x .(x2 – 3x + 1) d) y = )0(,sin
2
2 pi<<+ xx
x
3/ Cự trị của hàm số:
a) Dấu hiệu I: + Nếu f ’(x) ñổi dấu từ + sang - khi qua x0 thì x0 là ñiểm cực ñại
+ Nếu f ’(x) ñổi dấu từ - sang + khi qua x0 thì x0 là ñiểm cực tiểu
+ Nói chung nếu f ’(x) ñổi dấu khi qua x0 thì x0 là ñiểm cực trị
b) Dấu hiệu II:
≠
=
0)("
0)('
0
0
xf
xf
thì x0 là ñiểm cực trị của hs y = f(x)
>
=
0)("
0)('
0
0
xf
xf
thì x0 là ñiểm cực tiểu của hs y = f(x)
<
=
0)("
0)('
0
0
xf
xf
thì x0 là ñiểm cực ñại của hs y = f(x)
* Nếu hàm số y = f(x) có ñạo hàm tại x0 và ñạt cực trị tại x0 thì f ’(x0) = 0.
x
f’(x)
x0
+
-
0
Cð
x
f’(x)
x0
-
+
0
CT
x a b
f’(x) +
f(x)
Taøi lieäu oân thi toát nghieäp THPT – Ban Cô baûn Tröôøng THPT Lyù Töï Troïng
Taøi lieäu löu haønh noäi boä Bieân soaïn: Traàn Minh caûnh
2
Bài tập 1: Tìm các ñiểm cực trị nếu có của các hàm số:
a) y = xxx 154
3
1 23
−+− b) y = 2x3 + 3x2 – 36x – 10 c) y = x3(1 – x)2
d) y = x4 + 2x2 – 3 e) y = sin2x – x f) y = x2 – 5x + 5 + 2lnx
Bài tập 2:
a) Xác ñịnh m ñể hàm số y = (m + 2)x3 + 3x2 + mx – 5 có cực ñại và cực tiểu.
b) Tìm m ñể hàm số y = mx4 + (m2 – 9)x2 + 10 có 3 ñiểm cực trị.
c) Tìm a ñể hàm số y = ax3 – 2x2 + 3x – 1 ñạt cực trị tại x = - 1 .
d) Cho hàm số y = x3 – 6x2 + 9x (C). Với giá trị nào của m thì ñường thẳng y = x + m2 – m ñi
qua trung ñiểm của ñoạn thẳng nối 2 ñiểm cực ñại và cực tiểu của ñồ thị (C)?
e) Tìm m ñể hàm số y = x3 – mx2 + (m – 2/3)x + 5 có cực trị tại x = 1. Khi ñó hàm số hàm số ñạt
cực ñại hay cực tiểu tại x = 1. Hãy tính giá trị cực trị tương ứng?
f) Xác ñịnh m ñể hàm số y =
mx
mxx
+
++ 12
ñạt cực ñại tại x = 2.
f) Tìm a, b, c ñể ñồ thị hàm số y = x3 + ax2 + bx + c có các ñiểm cực trị là A(-2;16) và B(2;-16).
4/ Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) :
Trên khoảng (a,b) Trên ñoạn [a,b]
+ Tính ñạo hàm y’
+ Lập bảng biến thiên trên khoảng (a;b)
=>kết luận
Cách 1:
+ Tính ñạo hàm y’
+ Lập bảng biến thiên => kết luận
Cách 2:
+Tìm các ñiểm∈ [a,b] mà làm cho y’ bằng 0 hoặc
không xác ñịnh (giả sử là x1,x2, ,xn ∈ [a,b] )
+ Tính f(a), f(b), f(x1),f(x2),,f(xn)
+ So sánh các số này rồi kết luận.
Bài tập 1: Tìm GTLN, GTNN của các hàm số:
a) y= 4x3 – 3x4 b) y= x2 +
x
1
,(x>0) c) y = x +
x
4
, ( x > 0)
Bài tập 2: Tìm GTLN, GTNN của các hàm số:
a) y = x5 -5x3 +2 trên ñoạn [-2;3] b) y = x3 – 3x2 – 9x + 35 trên ñoạn [0;5]
c) y = x4 – 3x2 + 2 trên ñoạn [0;3] d) y=(x-6). 4x 2 + trên ñoạn [0,3]
e) y =
x
x
−
−
1
2
trên ñoạn [-3;-2] f) y = x45 − trên ñoạn [-1,1]
g) 3 22 3 12 1y x x x= − − + trên 52;
2
−
h/ 2.lny x x= trên ñoạn [ ]1;e
Bài tập 3: Tìm GTLN, GTNN của các hàm số: ( P2: ñặt ẩn phụ )
a) y= 2sin2x – cosx+1 b) y = 2sinx − xsin
3
4 3
trên ñoạn [0;pi], ( TN 03−04)
c) y = 4cos3x – 3cos4x d) y = 3sinx - cos2x + 2 trên ñoạn ]
2
;0[ pi
5/ Tiệm cận của ñồ thị hàm số:
Bài tập: Tìm các tiệm cận của ñồ thị các hàm số sau:
a) y = 2 1
2
x
x
−
+
b) y = 3 2
3 1
x
x
−
+
c) y = 5
2x
−
+
d) y =
2
632
+
++−
x
xx
6/ Khảo sát hàm số:
Bài tập : Khảo sát và vẽ ñồ thị các hàm số sau:
a) y = -x3 + 3x2 -3x -7 b) y = x3 -3x2 +1 c) y = 4x4 - 5x2 +1 d) y = x4 - 4x2 +4
e) y = x 2
x 2
+
−
f) y = 1 - 1
1 x−
g)y = 3 22 1x x x− + + h) y = -x3+3x2-3x -1
i) y = 4 21 3
4 2
x x− + j) y =
4
2 3
2 2
x
x+ − k) y = 3 1
2
x
x
+
−
f) y = 3
2
x
x
−
−
Taøi lieäu oân thi toát nghieäp THPT – Ban Cô baûn Tröôøng THPT Lyù Töï Troïng
Taøi lieäu löu haønh noäi boä Bieân soaïn: Traàn Minh caûnh
3
7/ Các vấn ñề liên quan ñến khảo sát hàm số:
Vấn ñề 1: Tiếp tuyến với ñồ thị
Dạng 1: Viết phương trình tiếp tuyến của (C): y = f(x) tại ñiểm M0(x0 ; y0) ( )C∈
Phương pháp:
Phương trình tiếp tuyến với (C) tại M(x0;y0) có dạng:
y - y0 = y’(x0).(x – x0)
Trong ñó :
x0: hoành ñộ tiếp ñiểm
y0: tung ñộ tiếp ñiểm và ñược tính y0 = f(x0)
y’(x0) : là ñạo hàm của hàm số y = f(x) tại x0 (cũng là hệ số góc k của tiếp tuyến)
Dạng 2: Viết phương trình tiếp tuyến của (C) : y = f(x) biết tiếp tuyến có hệ số góc k.
Phương pháp:
Gọi M0(x0 ; y0 ) là tiếp ñiểm. Phương trình tiếp tuyến của (C) tại M0 là:
y - y0 = y’(x0)(x – x0)
Giải phương trình y’(x0) = k tìm x0 và y0 => pt tiếp tuyến.
Chú ý:
+ Nếu tiếp tuyến // ñường thẳng y = ax + b thì hệ số góc tiếp tuyến k = a
+ Nếu tiếp tuyến ⊥ ñường thẳng y = ax + b thì hệ số góc tiếp tuyến k = 1
−
a
Dạng 3: Viết phương trình tiếp tuyến của (C) y = f(x) , biết tiếp tuyến ñi qua A(xA ; yA)
Phương pháp:
Gọi M0(x0 ; y0 ) là tọa ñộ tiếp ñiểm. Phương trình tiếp tuyến của (C) tại M0 là:
y - y0 = y’(x0)(x – x0)
Tiếp tuyến qua A nên ta có: yA - y0 = y’(x0)(xA – x0)
Giải phương trình tìm ñược x0 => f’(x0) => pt tiếp tuyến.
Bài tập 1: Cho (C) : y = x3 – 6x2 + 9x – 1. Viết phương trình tiếp tuyến của (C) :
a) Tại ñiểm có hoành ñộ bằng 1.
b) Tại ñiểm có tung ñộ bằng -1
c) Song song với ñường thẳng d1 : y = 9x – 5.
d) Vuông góc với ñường thẳng d2 : x + 24y – 1 = 0.
Bài tập 2: Cho (C) : y =
2
2
+
−
x
x
.Viết phương trình tiếp tuyến của (C):
a) Tại giao ñiểm của (C ) với trục Ox.
b) Song song với ñường thẳng d1 : y = 4x – 5.
c) Vuông góc với ñường thẳng d2: y = -x.
Bài tập 3:
a) Viết p.trình tiếp tuyến với ñồ thị (C): y = x3 – 3x + 2 mà ñi qua ñiểm A(1;0)
b) Viết p.trình tiếp tuyến với ñồ thị (C): y =
2
33
2
1 24 +− xx mà ñi qua ñiểm A(0; )2
3
c) Viết phương trình tiếp tuyến với ñồ thị (C): y =
2
2
−
+
x
x
mà ñi qua ñiểm A(-6;5)
Vấn ñề 2: Giao ñiểm ñồ thị (C) : y = f(x) và ñường thẳng (d) : y = ax + b
Phương pháp :
Hoành ñộ giao ñiểm của ñồ thị (C) và ñường thẳng (d) là nghiệm của phương trình:
f(x) = ax + b (1)
Do ñó : + Nghiệm của pt (1) là toạ ñộ giao ñiểm của (C) và (d).
+ Số nghiệm phân biệt của (1) bằng số giao ñiểm của (C) và (d).
Bài tập 1 : Tìm tọa ñộ giao ñiểm của hai ñồ thị:
a) (C):y = x3 + 4x2 + 4x + 1 và (d): y = x + 1 b) (C):
1
12
+
−
=
x
xy và 13:)( −−= xyd
Taøi lieäu oân thi toát nghieäp THPT – Ban Cô baûn Tröôøng THPT Lyù Töï Troïng
Taøi lieäu löu haønh noäi boä Bieân soaïn: Traàn Minh caûnh
4
Bài tập 2:
a) Tìm m ñể ñồ thị hàm số y = (x – 1) (x2 + mx + m) cắt trục hòanh tại ba ñiểm phân biệt
b) Tìm m ñể ñồ thị hàm số y = x4 – 2x2 – (m + 3) cắt trục hòanh tại 4 ñiểm phân biệt.
c) Tìm m ñể ñường thẳng y = mx + 2m + 2 cắt ñồ thị hàm số y =
1
12
+
−
x
x
tại 2 ñiểm phân biệt.
d) Tìm m ñể ñường thẳng ñi qua ñiểm A(-1;-1) và có hệ số góc là m cắt ñồ thị hàm số y =
12
2
+
+
x
x
tại hai ñiểm phân biệt.
Vấn ñề 3: Dùng ñồ thị (C): y = f(x) biện luận số nghiệm của một phương trình (*) nào ñó.
Phương pháp:
+ ðưa phương trình (*) về dạng: f(x) = h(m)
+ Số nghiệm của pt (*) là số giao ñiểm của ñồ thị (C) và ñường thẳng (d) : y = h(m).
+ Dựa vào ñồ thị kết luận.
Bài tập 1: Cho hàm số: y = 2x3 – 9x2 + 12x – 4 (C)
a) Khảo sát sự biến thiên và vẽ ñồ thị (C) của hàm số .
b) Biện luận theo m số nghiệm của phương trình: 2x3 – 9x2 + 12x – 4 – m = 0
Bài tập 2: Cho hàm số: y = x4 - 4x2 + 4 (C)
a) Khảo sát và vẽ ñồ thị (C) của ñồ thị hàm số.
b) Xác ñịnh tham số m ñể phương trình x4 - 4x2 + 4 – m = 0 có 4 nghiệm phân biệt.
Bài tập 3: Cho hàm số y = x3 – 3x2 (C)
a) Khảo sát và vẽ ñồ thị (C) của ñồ thị hàm số.
b) Xác ñịnh tham số m ñể phương trình x3 - 3x2 – m = 0 có 3 nghiệm phân biệt.
------o0o------
Taøi lieäu oân thi toát nghieäp THPT – Ban Cô baûn Tröôøng THPT Lyù Töï Troïng
Taøi lieäu löu haønh noäi boä Bieân soaïn: Traàn Minh caûnh
5
Chủ ñề 2: HÀM SỐ LUỸ THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARÍT
1/ Hàm số mũ:
Mũ Hàm số mũ y = ax , (a > 0, a 1≠ )
a0 = 1, 0≠∀a
a1 = a , a∀ TXð: D = R
am.an =am+n ðạo hàm : y’ = ax.lna
am/an = am-n
Tính ñơn ñiệu:
+ a >1: h/s ñồng biến trên R
+ 0<a<1: h/s nghịch biến trên R
an.bn =(ab)n Tiệm cận: trục Ox là tiệm cận ngang
an/bn = (a/b)n
(am)n = am.n
1 n
n
a
a
−
=
n ma = n
m
a
ðồ thị:
2/ Hàm số Lôgarít:
Lôgarít H/s Lôgarít: y = loga x , (a>0, a 1≠ )
loga1 = 0 và logaa = 1 TXð: D =R+
loga xa
= x, logaax = x ðạo hàm: y’ = ax ln.
1
log loga ax x
α α=
Tính ñơn ñiệu:
+ a>1: h/s ñồng biến trên R+
+ 0<a<1: h/s nghịch biến trên R+
1log logaa x xα α
=
Tiệm cận:
trục Oy là tiệm cận ñứng
loga(x.y) = loga x + loga y
log log loga a a
x
x y
y
= −
log .log loga b ab x x=
loglog
log
a
b
a
x
x
b
=
, 1log
logb a
a
b
=
ðồ thị:
3/ Phương trình Mũ và Lôgarít ñơn giản:
Mũ Lôgarít
logx aa b x b= ⇔ = log
b
a x b x a= ⇔ =
( ) ( ) ( ) ( )f x g xa a f x g x= ⇔ = ( ) 0log ( ) log ( ) ( ) ( )a a
f xf x g x f x g x
>
= ⇔
=
4/ Bất phương trình mũ và Lôgarít:
Mũ Lôgarít
a >1
log loga bx x aa b a a x b≥ ⇔ ≥ ⇔ ≥
( ) ( ) ( ) ( )f x g xa a f x g x≥ ⇔ ≥
log log log b b
a a a
x b x a x a≥ ⇔ ≥ ⇔ ≥
( ) 0
log ( ) log ( ) ( ) ( )a a
g xf x g x f x g x
>
≥ ⇔ ≥
0<a<1
log loga bx x aa b a a x b≥ ⇔ ≥ ⇔ ≤
( ) ( ) ( ) ( )f x g xa a f x g x≥ ⇔ ≤
log log log 0b b
a a a
x b x a x a≥ ⇔ ≥ ⇔ < ≤
( ) 0
log ( ) log ( ) ( ) ( )a a
f xf x g x f x g x
>
≥ ⇔ ≤
* Chú ý: Nếu pt hoặc bất pt chưa có những dạng trên thì trước hết ñặt ñiều kiện, sau ñó biến ñổi giải
y
x O
1
1
a
a>1
y
x O
1
1
a
0<a<1
y
x O
1
1 a
a>1
y
x
O
1
1
a
a>1
Taøi lieäu oân thi toát nghieäp THPT – Ban Cô baûn Tröôøng THPT Lyù Töï Troïng
Taøi lieäu löu haønh noäi boä Bieân soaïn: Traàn Minh caûnh
6
Dạng 1: Vẽ ñồ thị, tính ñạo hàm của hàm số mũ, logarit.
Bài tập 1: Vẽ ñồ thị c ... ối của hai ñường thẳng sau: (d):
1 2
1 3
5
x t
y t
z t
= +
= − +
= +
và (d’):
1 3 '
2 2 '
1 2 '
x t
y t
z t
= +
= − +
= − +
Bài tập 4:
a) Chứng minh ñường thẳng (d): 1
2 2
4 3
x t
y t
z t
= +
= +
= +
vuông góc với mp(P): 2x + 4y + 6z + 9 = 0
b) Chứng minh 2 ñường thẳng sau ñây vuông góc: (d):
5
3 2
4
x t
y t
z t
= −
= − +
=
và (d’):
9 2 '
13 3 '
1 '
x t
y t
z t
= +
= +
= −
5) Dạng 5: Tìm toạ ñộ hình chiếu của một ñiểm M lên một mp (P), ñiểm ñối xứng qua mphẳng
* Phương pháp:
P
H
M
Bài tập :
a) Tìm toạ ñộ hình chiếu của ñiểm M(1;-2;4) lên mp(P): 2x + y – 3z + 1 = 0
b) Tìm toạ ñộ hình chiếu của ñiểm A(2;-2;1) lên mp(P): x + 2y – 5z + 2 = 0
c) Tìm toạ ñộ ñiểm A’ ñối xứng với ñiểm A(2;-2;1) qua mp(P) : 3x – y + z + 2 = 0
d) Tìm toạ ñộ ñiểm N’ ñối xứng với ñiểm N(5;-2;0) qua mp(P) : 3x + 2y + z - 4 = 0
6) Dạng 6: Bài toán liên quan ñến mặt cầu:
* Kiến thức: Phương trình mặt cầu
Dạng (1) Dạng (2)
(x – x0)2 + (y – y0)2 + (z – z0)2 = R2 x2 + y2 + z2 + 2ax + 2by + 2cz + d = 0
Tâm: I(x0; y0;z0) Bán kính: R Tâm: I(-a; -b; -c) Bán kính: R = 2 2 2a b c d+ + −
* ðiều kiện tiếp xúc giữa một mặt phẳng (P) và mặt cầu (S) có tâm I, bán kính R:
d=R
P
H
I
Bài tập 1: Lập phương trình mặt cầu (S), biết:
a/ (S) ði qua ñiểm A(5;-2;1) và có tâm I(3;-3;1).
b/ (S) có ñường kính là AB với A(6; 4;-3), B(2;8;1).
c/ (S) có tâm I (–2; 1; 1) và tiếp xúc với mp (P): x + 2y – 2z + 5 = 0.
d) (S) qua 4 ñiểm: A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-2).
e) (S) qua 4 ñiểm: A(1;2;-1), B(2;-1;3), C(-2;3;3) và gốc toạ ñộ O.
f/ Qua 3 ñiểm A(1; 2;– 4), B(1; –3;1), C(2;2;3) và có tâm nằm trên mp(Oxy).
* Gọi H là hình chiếu của M lên mp(P)
+ Viết pt của ñường thẳng MH
( qua M và nhận ( )Pn
làm VTCP).
+ Toạ ñộ của H là nghiệm của hệ 2 pt:
(gồm pt của mp(P) và pt của ñ.thẳng MH),
giải hệ suy ra toạ ñộ của hình chiếu H.
( )Pn
( )d I,(P) R=
Taøi lieäu oân thi toát nghieäp THPT – Ban Cô baûn Tröôøng THPT Lyù Töï Troïng
Taøi lieäu löu haønh noäi boä Bieân soaïn: Traàn Minh caûnh
21
Bài tập 2:
a) Viết pt mặt phẳng (P) tiếp xúc với mặt cầu (S): (x-3)2 + (y+4)2 + z2 = 4 tại ñiểm A(3;-4;2)
b) Viết pt mặt phẳng (P) song song với mp(Q): 2x – 3y + z – 2 = 0 và tiếp xúc với mặt cầu :
(S): x2 + y2 + z2 – 2x + 4y – 6z + 5 = 0.
c) Viết pt mặt phẳng (P) song song với 2 ñường thẳng (d):
+−=
−=
+−=
tz
ty
tx
213
31
25
, (d’):
+=
−−=
+−=
tz
ty
tx
8
21
37
ñồng thời tiếp xúc với mặt cầu (S): (x-3)2 + (y + 4)2 + z2 = 42.
7) Dạng 7: Bài toán tổng hợp .
Bài tập 1: Tìm toạ ñộ của các véctơ sau: 2a i j
→ → →
= − + ; 7 8b i k
→ → →
= − ; 9c k
→ →
= − ; 3 4 5d i j k
→ → → →
= − +
Bài tập 2: Cho hình hộp ABCD.A'B'C'D', biết A(1; 0; 1), B(2; 1; 2), D(1; -1; 1), C'(4; 5; -5). Tìm toạ ñộ
các ñỉnh còn lại.
Bài tập 3: Cho bốn ñiểm A(-2;6;3), B(1;0;6), C(0;2;-1), D(1;4;0)
a) Viết pt mặt phẳng (BCD) . Từ ñó chứng minh A, B, C, D là bốn ñỉnh của một tứ diện.
b) Tính cosin góc giữa 2 ñường thẳng AB và CD.
c) Tính ñộ dài ñường cao xuất phát từ ñỉnh A của tứ diện ABCD.
d) Viết pt mặt phẳng (P) chứa AB và song song với CD.
Bài tập 4: Cho các ñiểm A(-2;6;3), B(1;0;6), C(0;2;-1).
a) Tìm toạ ñộ ñiểm D sao cho ABCD là hình bình hành.
b) Tìm toạ ñộ ñiểm K sao cho 2AK AB BC= +
c) Gọi N là ñiểm sao cho 2NB NC= −
. Viết phương trình mặt phẳng (P) qua N và vuông góc với
ñường thẳng BC.
Bài tập 5: Trong không gian Oxyz cho:
mp(P): 2x – y + 2z + 11 = 0, 2 ñiểm: M(1;-1;2), N(2;-1;3), ñường thẳng (d):
1 2
1 3
5
x t
y t
z t
= +
= − +
= +
a) Tìm toạ ñộ giao ñiểm của (d) và mp(P).
b) Viết pt mặt phẳng (Q) chứa M và vuông góc với (d).
c) Viết pt ñường thẳng (d’) qua M và vuông góc với mp(P).
d) Tìm toạ ñộ hình chiếu H của ñiểm M lên mp(P).
e) Tìm toạ ñộ ñiểm N’ ñối xứng với N qua mp(P).
f) Viết phương trình mặt cầu (S) có tâm M và qua ñiểm N.
g) Viết pt mặt cầu (S) có tâm M và tiếp xúc với mp(P).
------o0o------
Taøi lieäu oân thi toát nghieäp THPT – Ban Cô baûn Tröôøng THPT Lyù Töï Troïng
Taøi lieäu löu haønh noäi boä Bieân soaïn: Traàn Minh caûnh
22
MỘT SỐ ðỀ THI MẪU
ðề số 1 (Thời gian làm bài:150 phút)
I- PHẦN CHUNG CHO TẤT CẢ THÍ SINH: (7.0 ñiểm)
Câu I: (3.0 ñiểm)
Cho hàm số = − + −4 22 1y x x , có ñồ thị (C)
1) Khảo sát và vẽ ñồ thị (C) của hàm số.
2) Viết pttt với (C) tại ñiểm có hoành ñộ 2x =
Câu II: (3.0 ñiểm)
1) Giải bất phương trình: 2
3
2 3log 0
1
x
x
−
<
+
2) Tính tích phân: os
pi
+∫
32
0
2
1 sin
c xdx
x
3) Tìm GTLN và GTNN của hàm số y = x3 + 3x2 – 9x – 5 trên ñoạn 50;
2
.
Câu III: (1.0 ñiểm)
Cho hình nón tròn xoay có ñỉnh là S, ñường tròn ñáy có tâm O, ñộ dài
ñường sinh l a= , góc hợp bởi ñường sinh và mặt phẳng chứa ñường tròn ñáy là
4
pi
. Tính diện tích xung quanh và diện tích toàn phần của hình nón theo a .
II. PHẦN RIÊNG: (3.0 ñiểm)
(Thí sinh học chương trình nào thì chỉ ñược làm phần dành riêng cho chương trình ñó)
1) Theo chương trình chuẩn:
Câu IV.a: (2.0 ñiểm)
Trong không gian với hệ tọa ñộ Oxyz, cho:
mặt phẳng (P): 3 2 3 7 0x y z− − − = , và ñiểm A(3;- 2;- 4).
1) Tìm tọa ñộ ñiểm A’ là hình chiếu của A trên (P).
2) Viết phương trình mặt cầu có tâm A và tiếp xúc với (P).
Câu V.a: (1.0 ñiểm)
Cho số phức 1 3
2 2
z i= − + . Hãy tính: 2 1z z+ +
2) Theo chương trình nâng cao:
Câu IV.b: (2.0 ñiểm)
Trong không gian với hệ tọa ñộ Oxyz, cho:
mặt phẳng (P): 2 2 5 0x y z− + + = và các ñiểm A(0;0;4), B(2;0;0)
1) Viết phương trình mặt phẳng chứa AB và vuông góc với mặt phẳng (P).
2) Viết phương trình mặt cầu ñi qua O, A, B và tiếp xúc với mặt phẳng (P).
Câu V.b: (1.0 ñiểm)
Tìm ,x y sao cho: 2( 2 ) 3x i x yi+ = − +
___________________________
Taøi lieäu oân thi toát nghieäp THPT – Ban Cô baûn Tröôøng THPT Lyù Töï Troïng
Taøi lieäu löu haønh noäi boä Bieân soaïn: Traàn Minh caûnh
23
ðề số 2 (Thời gian làm bài:150 phút)
I- PHẦN CHUNG CHO TẤT CẢ THÍ SINH: (7.0 ñiểm)
Câu I: (3.0 ñiểm)
Cho hàm số y = - x3 + 3x2
1) Khảo sát và vẽ ñồ thị (C) của hàm số.
2) Biện luận theo m số nghiệm của phương trình: - x3 + 3x2 – m = 0.
Câu II: (3.0 ñiểm)
1) Giải phương trình: 2 22 9.2 2 0x x+ − + =
2) Tính tích phân: I =
1
0
(2 1). .xx e dx+∫
3) Tính diện tích hình phẳng giới hạn bởi ñồ thị hàm số y = x3 - 3x2 và trục Ox
Câu III: (1.0 ñiểm)
Cho hình chóp S.ABCD có ñáy ABCD là hình vuông cạnh a, cạnh bên SA
vuông góc với ñáy, cạnh bên SB = a 3 . Tính thể tích khối chóp S.ABCD và chứng
minh trung ñiểm của SC là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD.
II. PHẦN RIÊNG: (3.0 ñiểm)
(Thí sinh học chương trình nào thì chỉ ñược làm phần dành riêng cho chương trình ñó)
1) Theo chương trình chuẩn:
Câu IV.a: (2.0 ñiểm)
Trong không gian Oxyz, cho 3 ñiểm A(-1;1;2), B(0;1;1), C(1;0;4).
1) Chứng minh ∆ ABC vuông. Viết p. trình tham số của ñường thẳng AB.
2) Gọi M là ñiểm sao cho 2MB MC= − , viết phương trình mặt phẳng (P) ñi
qua M và vuông góc với BC.
Câu V.a: (1.0 ñiểm)
Giải phương trình sau trong tập số phức: 2x2 – 5x + 4 = 0
2) Theo chương trình nâng cao:
Câu IV.b: (2.0 ñiểm)
Trong không gian Oxyz, cho 3 ñiểm A(2;0;0), B(0;3;0), C(0;0;6).
1) Viết phương trình mặt phẳng (ABC) và tính diện tích tam giác ABC.
2) Gọi G là trọng tâm ∆ ABC, viết phương trình mặt cầu ñường kính OG.
Câu V.b: (1.0 ñiểm)
Tìm môñun của số phức 2(2 )( 3 2 )z i i= − − + .
_______________________________
Taøi lieäu oân thi toát nghieäp THPT – Ban Cô baûn Tröôøng THPT Lyù Töï Troïng
Taøi lieäu löu haønh noäi boä Bieân soaïn: Traàn Minh caûnh
24
ðề số 3 (Thời gian làm bài:150 phút)
I- PHẦN CHUNG CHO TẤT CẢ THÍ SINH: (7.0 ñiểm)
Câu I: (3.0 ñiểm)
Cho hàm số y = x3 –3x – 1 (1)
1) Khảo sát vẽ ñồ thị (C) của hàm số.
2) Viết phương trình ñường thẳng (d) vuông góc với ñường thẳng y =
3
x
và
tiếp xúc với ñồ thị (C) của hàm số.
Câu II: (3.0 ñiểm)
1) Giải phương trình 16x –17.4x +16 = 0
2) Tính tích phân ( ) dxxx∫ +
2
0
sin12
pi
3) Tìm giá trị lớn nhất của biểu thức: y = ( ) x2sin5,0
Câu III: (1.0 ñiểm)
Cho hình chóp tam giác S.ABC có SA, SB, SC ñôi một vuông góc nhau và
SA = a, SB = b, SC = c. Tính ñộ dài ñường cao vẽ từ S của hình chóp S.ABC.
II. PHẦN RIÊNG: (3.0 ñiểm)
(Thí sinh học chương trình nào thì chỉ ñược làm phần dành riêng cho chương trình ñó)
1) Theo chương trình chuẩn:
Câu IV.a: (2.0 ñiểm)
Trong không gian Oxyz cho ñường thẳng (d):
−=
+−=
+=
tz
ty
tx
3
1
21
1) Viết phương trình mặt phẳng (P) ñi qua A(2;0;0) và vuông góc với
ñường thẳng (d)
2) Tìm tọa ñộ giao ñiểm của (d) với mặt phẳng (P).
Câu V.a: (1.0 ñiểm)
Giải phương trình sau trên tập số phức: ( ) 223232 iixi +=+−
2) Theo chương trình nâng cao:
Câu IV.b: (2.0 ñiểm)
Trong không gian Oxyz cho ñường thẳng (d):
−=
+−=
+=
tz
ty
tx
3
1
21
1) Tìm tọa ñộ hình chiếu vuông góc của ñiểm A(2;0;-1) lên ñường thẳng (d)
2) Tìm tọa ñộ ñiểm B ñối xứng của A qua ñường thẳng (d).
Câu V.b: (1.0 ñiểm)
Tìm giá trị lớn nhất của biểu thức: xxy +−= 3
___________________________
Taøi lieäu oân thi toát nghieäp THPT – Ban Cô baûn Tröôøng THPT Lyù Töï Troïng
Taøi lieäu löu haønh noäi boä Bieân soaïn: Traàn Minh caûnh
25
ðề số 4 (Thời gian làm bài:150 phút)
I- PHẦN CHUNG CHO TẤT CẢ THÍ SINH: (7.0 ñiểm)
Câu I: (3.0 ñiểm)
Cho hàm số
2
2
+
+−
=
x
xy .
1) Khảo sát sự biến thiên và vẽ ñồ thị (C) của hàm số ñã cho.
2) Viết phương trình tiếp tuyến của (C), biết nó vuông góc với ñường thẳng
42
2
1
−= xy .
Câu II: (3.0 ñiểm)
1) Giải phương trình : 09.66.134.6 =+− xxx
2) Tính tích phân :
2
3 2
0
3 4.I x x dx= +∫
3) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số : 3coscos)( 2 ++= xxxf .
Câu III: (1.0 ñiểm)
Cho khối chóp tam giác ñều S.ABC có ñáy ABC là tam giác ñều cạnh a và
các cạnh bên tạo với ñáy một góc 600. Hãy tính thể tích của khối chóp ñó.
II. PHẦN RIÊNG: (3.0 ñiểm)
(Thí sinh học chương trình nào thì chỉ ñược làm phần dành riêng cho chương trình ñó)
1) Theo chương trình chuẩn:
Câu IV.a: (2.0 ñiểm)
Trong không gian với hệ trục tọa ñộ Oxyz, cho các ñiểm:
A(1;0;2), B(-1;1; 5), C(0;-1;2) và D(2;1 ;1)
1) Lập phương trình mặt phẳng (P) chứa AB và song song với CD.
2) Viết phương trình mặt cầu (S) ñi qua 4 ñiểm A, B, C, D.
Câu V.a: (1.0 ñiểm)
Tìm môñun của số phức
i
i
z
−
−−
=
1
38
2) Theo chương trình nâng cao:
Câu IV.b: (2.0 ñiểm)
Trong không gian với hệ trục tọa ñộ Oxyz, cho ñường thẳng (d) và mặt
phẳng (α ) lần lượt có phương trình :
3
1
2
3
1
5
:)( −=+=
−
− zyxd , ( ) 022: =−−+ zyxα
1) Viết phương trình mặt phẳng ( β ) ñi qua giao ñiểm I của (d) và (α ) và
vuông góc (d).
2) Cho A(0;1;1). Hãy tìm toạ ñộ ñiểm B sao cho (α ) là mặt trung trực của
ñoạn AB.
Câu V.b: (1.0 ñiểm)
Tìm số phức z sao cho 13 =
+
+
iz
iz
và z + 1 có acgumen bằng
6
pi
− .
Tài liệu đính kèm:
 On TNghiep 6 chu de CB.pdf
On TNghiep 6 chu de CB.pdf





