Phương trình mũ và logarit (Lê Quang Dũng)

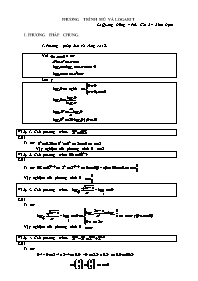
PHƯƠNG TRÌNH MŨ VÀ LOGARIT
Lê Quang Dũng – Phù Cát 2 – Bình Định 
I. PHƯƠNG PHÁP CHUNG.
	1. Phương pháp đưa về cùng cơ số:
Với ta có:
	+ 
	+ 
	+ 
Lưu ý
	+ có nghĩa 
	+ 
	+ 
	+ 
Ví dụ 1: Giải phương trình: 
Giải
	Ta có: 
Vậy nghiệm của phương trình là 
Ví dụ 2: Giải phương trình 
Giải
	Ta có: 
	Vậy nghiệm của phương trình là 
Ví dụ 3: Giải phương trình: 
Giải
	Ta có: 
	Vậy nghiệm của phương trình là 
Ví dụ 4: Giải phương trình: 
Giải
	Ta có:
	Vậy nghiệm của phương trình là 
Ví dụ 5: Giải phương trình: 
Giải
Phương trình đã cho tương đương với:
	Vậy nghiệm của phương trình là 
Ví dụ 6: Giải phương trình: 
Giải
	Ta có: 
	Vậy nghiệm của phương trình là 
Ví dụ 7: Giải phương trình: 
Giải
	Điều kiện: 
	Khi đó ta có: 
	Nhận nghiệm 
	Vậy nghiệm của phương trình là 
Ví dụ 8:Giải phương trình: 
Giải
	Điều kiện: 
	Khi đó ta có: 
	Vậy nghiệm của phương trình là 
Ví dụ 10: Giải phương trình: 
Giải
	Phương trình đã cho tương đương với hệ sau:
	Vậy nghiệm của phương trình là 
	2. Phương pháp mũ hóa hoặc logarit hóa:
Để giải phương trình bằng phương pháp mũ hóa hoặc logarit hóa chúng ta phải nắm vững các tính chất đã nêu ở mục 1. Tuy nhiên trước khi mũ hóa hoặc lgarit hóa, chúng ta cần biến đổi để rút gọn cả hai vế của phương trình về dạng gọn nhất. Phương pháp logarit hóa tỏ ra càng hiệu lực khi hai vế của phương trình có dạng tích của các lũy thừa.
Ví dụ 1: Giải phương trình: 
Giải
	Điều kiện: .
	Khi đó, lấy logarit thập phân hai vế ta dược:
	Vậy nghiệm của phương trình là 
Ví dụ 2: Giải phương trình: 
Giải
	Điều kiện: .
	Khi đó phương trình đã cho tương đương với:
	So sánh với điều kiện ban đầu, suy ra không có giá trị thỏa mãn.
	Vậy phương trình đã cho vô nghiệm.
Ví dụ 3: Giải phương trình: 
Giải
	Điều kiện: 
	Khi đó phương trình đã cho tương đương với:
	So sánh với điều kiện ban đầu nhận nghiệm 
	Vậy nghiệm của phương trình là .
Ví dụ 4: Giải phương trình: 
Giải
	Điều kiện: 
	Khi đó phương trình đã cho tương đương với: 
	So sánh với điều kiện ban đầu nhận nghiệm 
	Vậy nghiệm của phương trình là .
Ví dụ 5: Giải phương trình: 
Giải
	Phương trình đã cho tương đương với:
	Điều kiện: 
	Khi đó phương trình đã cho tương đương với: 
	So sánh với điều kiện (*) ta nhận 
	Vậy nghiệm của phương trình là .
	3. Phương pháp đặt ẩn phụ:
Nếu một phương trình mũ hay logarit sau khi rút gọn có dạng hoặc trong đó là một hàm số theo ta sẽ đặt hoặc . Khi đó ta sẽ được phương trình đại số , giải phương trình này nếu có nghiệm ta sẽ tìm được nghiệm . Phương pháp này được gọi là phương pháp đặt ẩn phụ.
Ví dụ 9: Giải phương trình: a) b) 
Giải
Đặt . 
	Khi đó phương trình đã cho tương đương với:
	Do nên nhận .
	Suy ra: 
	Vậy nghiệm của phương trình là 
Điều kiện: 
	Chia hai vế của phương trình cho , ta được:
	Đặt , ta được phương trình:
	Khi đó: 
	Vậy nghiệm của phương trình là
Ví dụ 2: Giải phương trình: 
Giải
	Biến đổi phương trình đã cho về dạng: 
	Đặt . Khi đó phương trình đã cho tương đương với: 
	Suy ra 
	Vậy nghiệm của phương trình là .
Ví dụ 3: Giải phương trình: 
Giải
	Điều kiện:
	Biến đổi phương trình đã cho về dạng: 
	Đặt . Khi đó ta nhận được phương trình: 
	Với 
	Với 
	Vậy nghiệm của phương trình đã cho là 
Ví dụ 4: Giải phương trình: 
Giải
	Điều kiện: 
	Biến đổi phương trình về dạng:
	Đặt 
	Khi đó phương trình tương đương với:
	So sánh với điều kiện ban đầu nhận nghiệm 
	Suy ra 
	Vậy nghiệm của phương trình đã cho là 
Ví dụ 5: Giải phương trình: 
Giải
	Áp dụng qui tắc 
	Điều kiện: 
	Biến đổi phương trình về dạng: 
	Đặt .
	Khi đó phương trình tương đương với:
	Với 
	Với 
	Vậy nghiệm của phương trình đã cho là 
Ví dụ 6: Giải phương trình: 
Giải
	Điều kiện: 
	Biến đổi phương trình về dạng: 
	Đặt 
	Khi đó phương trình tương đương với:
	So sánh với điều kiện ban đầu nhận nghiệm 
	Suy ra 
	Vậy nghiệm của phương trình đã cho là 
Ví dụ 7:Giải phương trình: 
Giải
	Điều kiện: 
	Khi đó phương trình đã cho tương đương với:
	Đặt . Khi đó ta có: 
	Với . So sánh với điều kiện nhận nghiệm 
	Với . So sánh với điều kiện loại cả hai nghiệm này.
	Vậy nghiệm của phương trình đã cho là .
Ví dụ 8: Tìm tất cả các nghiệm thuộc đoạn của phương trình .
Giải
	Áp dụng công thức 
	Biến đổi phương trình về dạng:
	Đặt 
	Khi đó phương trình tương đương với:
	So sánh với điều kiện ta nhận nghiệm 
	Suy ra:
	Hay 
	Do nên chỉ có thỏa mãn.
	Vậy phương trình đã cho có hai nghiệm là 
	4. Sử dụng tính chất của hàm số:
	Có một số phương trình không thể dùng thuần túy các phương pháp trên, đôi khi cần phải dùng các tính chất của bất đẳng thức để giải, hoặc phát hiện tập hợp chứa nghiệm rồi thử nghiệm, hoặc phát hiện nghiệm rồi chứng minh nghiệm đó là duy nhất hoặc sử dụng tính chất đồng biến, nghịch biến của hàm số.
Ví dụ 1: Giải phương trình: 
Giải
	Ta có nhận xét sau:
	Vậy phương trình đã cho vô nghiệm.
Ví dụ 2: Giải phương trình: 
Giải
	Điều kiện: 
	Từ đó, nghiệm của phương trình chỉ có thể là hoặc 
	Với , thay vào phương trình ban đầu ta được:
	phương trình thỏa mãn
	Với , thay vào phương trình ban đầu ta được:
	Nhận xét: Vì nên , suy ra phương trình không thỏa mãn.
	Vậy nghiệm của phương trình đã cho là .
Ví dụ 3: Giải phương trình: 
Giải
	Chia hai vế của phương trình cho ta được:
	 (1)
	Nhận thấy rằng là nghiệm của phương trình đã cho.
	Ta sẽ chứng minh là nghiệm duy nhất của phương trình này.
	Thật vậy:
	Đặt và 
	Dễ dàng thấy rằng là hàm nghịch biến và là hàm hằng. Do đó đồ thị của hai hàm số này sẽ cắt nhau tại một điểm duy nhất và điểm đó có hoành độ là .
	Vậy phương trình đã cho có duy nhất một nghiệm là .
Ví dụ 4: Cho là độ dài 3 cạnh của một tam giác vuông có cạnh huyền bằng . Giải các phương trình: 
	a. 	b. 
Giải
	a. Do là độ dài 3 cạnh của một tam giác vuông có cạnh huyền bằng nên ta có:
	Suy ra là một nghiệm của phương trình 
	Ta lại có: 
	Vì nên các hàm số nghịch biến. 
	Suy ra, nghịch biến trên .
	Hay là ngiệm duy nhất của phương trình .
	b. Đặt . Khi đó phương trình đã cho tương đương với:
	Theo câu a phương trình này có duy nhất một nghiệm là 
	Suy ra .
	Vậy phương trình có duy nhất một nghiệm là .
Ví dụ 5: Giải phương trình: 
Giải
	Điều kiện: .
	Biến đổi phương trình đã cho về dạng:
	So sánh với điều kiện ban đầu nhận nghiệm 
	Vậy nghiệm của phương trình đã cho là .
Ví dụ 6: Tìm tất cả các cặp số thực thỏa mãn (1) và (2)
Giải
	Ta có:
	(*)
	Với thay vào (2) ta được:
	(**)
	Từ (*) và (**) ta có 
	Thay vào (1) ta được 
	Vậy có hai cặp số thỏa mãn yêu cầu đề bài là và .
Ví dụ 7: Giải phương trình: 
Giải
	Đặt , khi đó ta nhận được phương trình:
	Ta xem phương trình trên là phương trình bậc hai theo có hai nghiệm là:
	Ta chỉ nhận nghiệm với điều kiện 
	Suy ra . Nhận thấy rằng là nghiệm của phương trình này.
	Thật vậy:
	Nếu ta có: nên phương trình vô nghiệm.
	Nếu ta có: nên phương trình vô nghiệm.
	Vậy phương trình đã cho có duy nhất một nghiệm là .
Ví dụ 8: Tìm số nguyên thỏa mãn 
Giải
	Với : Đây không là nghiệm của phương trình đã cho.
	Với : Lấy logarit thập phân hai vế ta có:
	 do 
	Với : Nếu là số nguyên chẵn thì là số lẻ, suy ra hay phương trình đã cho vô nghiệm. Do đó phải là số nguyên lẻ.
	Ta thấy là hai nghiệm của phương trình.
	Xét , lúc này:
	 không thỏa.
	Vậy phương trình đã cho có ba nghiệm phân biệt là .
III. BÀI TẬP VẬN DỤNG 
Bài 1: Giải phương trình: 
	a. 	b. 
	c. 	d. 
	e. 	f. 
Bài 2: Giải phương trình: 
	a. 	
	b. 
	c. 
	d. 
	e. 
	f. 
Bài 3: Giải phương trình: 
	a. 	b. 
	c. 	d. 
	e. 
Bài 4: Giải phương trình: 
	a. 	b. 
	c. 
Bài 5: Giải phương trình: 
Bài 6: Giải phương trình: 
	a. 	b. 
	c. 	d. 
	e. 	f. 
	g. 	h. 
	i. 
Bài 7: Giải phương trình: 
	a. 	b. 
	c. 	d. 
Bài 8: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
	e. 
Bài 9: Giải phương trình: 
	a. 	b. 
	c. 	d. 
	e. 	f. 
Bài 10: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
Bài 11: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
	e. 
Bài 12: Giải phương trình: 
	a. 	b. 
	c. 	d. 
Bài 13: Giải phương trình: 
	a. 	b. 
	c. 	d. 
Bài 14: Giải phương trình: 
	a. 	b. 
	c. 	d. 
Bài 15: Giải phương trình: 
	a. 	b. 
	c. 	d. 
Bài 16: Giải phương trình: 
	a. 	b. 
	c. 	d. 
Bài 17: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
Bài 18: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
Bài 19: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
Bài 20: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
Bài 21: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
Bài 22: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
Bài 23: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
Bài 24: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
Bài 25: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
Bài 26: Giải phương trình: 
	a. 
	b. 
	c. 
	d. 
Bài 27: Giải phương trình: 
	a. 
	b. 
	c. 
	d.