Một số phương pháp giải Phương trình− Bất phương trình− Hệ phương trình mũ-logarit

Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 1
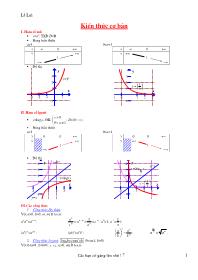
KiÕn thøc c¬ b¶n 
I .Hàm số mũ 
• y=ax; TXĐ D=R 
• Bảng biến thiên 
a>1 0<a<1 
x 
−∞ 0 +∞ x −∞ 0 +∞ 
y +∞ 
1 
 −∞ 
 y +∞ 
1 
 −∞ 
• Đồ thị 
-3 -2 -1 1
-2
-1
1
2
3
x
y
y=3x
-2 -1 1 2 3
-2
-1
1
2
3
x
y
x
y 





=
3
1
II .Hàm số lgarit 
• y=logax, ĐK:



≠<
>
10
0
a
x
; D=(0;+∞) 
• Bảng biến thiên 
a>1 0<a<1 
x 0 0 +∞ x 0 0 +∞ 
y +∞ 
1 
 −∞ 
 y +∞ 
1 
 −∞ 
• Đồ thị 
-1 1 2 3
-2
-1
1
2
3
4
x
y
y=x
y=3x
y=log3x
-1 1 2 3
-2
-1
1
2
3
4
x
y
x
y 





=
3
1
xy
3
1log=
y=x
III.Các công thức 
1. Công thức lũy thừa: 
Với a>0, b>0; m, n∈R ta có: 
a
n
a
m 
=a
n+m; mn
m
n
a
a
a
−
= ;(
na
1
=a−m ; a0=1; a−1=
a
1 ); 
(an)m =anm ; (ab)n=anbn; 
m
nn
b
a
b
a
=




 ; n mn
m
aa = . 
2. Công thức logarit: logab=c⇔ac=b (00) 
Với 00; α∈R ta có: 
Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 2
loga(x1x2)=logax1+logax2 ; loga
2
1
x
x
= logax1−logax2; 
xa
xa
=
log ; logaxα=αlogax; 
xx aa log
1log
α
α = ;(logaax=x); logax=
a
x
b
b
log
log
;(logab=
ablog
1 ) 
logba.logax=logbx; alogbx=xlogba. 
IV.Phương trình và bất phương trình mũ−logarit 
1. Phương trình mũ−logarit 
a. Phương trình mũ: 

Đưa về cùng cơ số 
+0<a≠1: af(x)=ag(x) (1) ⇔ f(x)=g(x). 
+ 0<a≠1: af(x)=b ⇔ ( )

=
>
bxf
b
alog
0
. 
Chú ý: Nếu a chứa biến thì (1) ⇔(a−1)[f(x)−g(x)]=0 

Đặt ẩn phụ: Ta có thể đặt t=ax (t>0), để đưa về một phương trình đại số.. 
Lưu ý những cặp số nghịch đảo như: (2 3± ), (7 4 3± ), Nếu trong một phương trình có chứa {a2x;b2x;axbx} ta có 
thể chia hai vế cho b2x(hoặc a2x) rồi đặt t=(a/b)x (hoặc t=(b/a)x. 

Phương pháp logarit hóa: af(x)=bg(x)⇔ f(x).logca=g(x).logcb,với a,b>0; 0<c≠1. 
b. Phương trình logarit: 

Đưa về cùng cơ số: 
+logaf(x)=g(x)⇔ ( ) ( )

=
≠<
xgaxf
a 10
 +logaf(x)= logag(x)⇔ ( ) ( )[ ]
( ) ( )



=
>>
≠<
xgxf
xgxf
a
00
10
. 

Đặt ẩn phụ. 
2. Bất phương trình mũ−logarit 
a. Bất phương trình mũ: 

 af(x)>ag(x) ⇔ ( ) ( ) ( )[ ]

>−−
>
01
0
xgxfa
a
; 
 af(x)≥ag(x) ⇔ ( ) ( ) ( )[ ]

≥−−
>
01
0
xgxfa
a
. 
Đặt biệt: 
* Nếu a>1 thì: af(x)>ag(x) ⇔ f(x)>g(x); 
a
f(x)≥ag(x) ⇔ f(x)≥g(x). 
* Nếu 0ag(x) ⇔ f(x)<g(x); 
 a
f(x)≥ag(x) ⇔ f(x)≤g(x). 
b. Bất phương trình logarit: 

logaf(x)>logag(x)⇔ ( ) ( )
( ) ( ) ( )[ ]



>−−
>>
≠<
01
0,0
10
xgxfa
xgxf
a
; 
logaf(x)≥logag(x)⇔ ( ) ( )
( ) ( ) ( )[ ]



≥−−
>>
≠<
01
0,0
10
xgxfa
xgxf
a
. 
Đặt biệt: 
+ Nếu a>1 thì: logaf(x)>logag(x) ⇔ ( ) ( )( )

>
>
0xg
xgxf
; 
+ Nếu 0logag(x) ⇔ ( ) ( )( )

>
<
0xf
xgxf
. 
Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 3
 MỘT SỐ PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH−BẤT PHƯƠNG TRÌNH−HỆ 
PHƯƠNG TRÌNH MŨ-LOGARIT 
I. Biến đổi thành tích 
Ví dụ 1: Giải phương trình: ( ) ( )2 2 22 22 4.2 2 4 0 2 1 . 2 4 0x x x x x x x x+ − −− − + = ⇔ − − = . 
Nhận xét: Mặc dù cùng cơ số 2 nhưng không thể biến đổi để đặt được ẩn phụ do đó ta phải phân tích thành 
tích: ( ) ( )2 22 1 . 2 4 0x x x− − − = . Đây là phương trình tích đã biết cách giải. 
Ví dụ 2: Giải phương trình: ( ) ( )29 3 32 log log .log 2 1 1x x x= + − . 
Nhận xét: Tương tự như trên ta phải biến đổi phương trình thành tích: ( )3 3 3log 2 log 2 1 1 .log 0x x x − + − =  . 
Đây là phương trình tích đã biết cách giải. 
Tổng quát: Trong nhiều trường hợp cùng cơ số nhưng không thể biến đổi để đặt ẩn phụ được thì ta biến đổi thành 
tích. 
II. Đặt ẩn phụ-hệ số vẫn chứa ẩn 
Ví dụ 1: Giải phương trình: 9 2( 2)3 2 5 0x xx x+ − + − = . Đặt t = 3x (*), khi đó ta có: 
( )2 2 2 2 5 0 1, 5 2t x t x t t x+ − + − = ⇒ = − = − . Thay vào (*) ta tìm được x. 
Lưu ý: Phương pháp này chỉ sử dụng khi ∆ là số chính phương. 
Ví dụ 2: Giải phương trình: ( ) ( ) ( )23 3log 1 5 log 1 2 6 0x x x x+ + − + − + = . Đặt t = log3(x+1), ta có: 
( )2 5 2 6 0 2, 3t x t x t t x+ − − + = ⇒ = = − ⇒ x = 8 và x = 2. 
III. Phương pháp hàm số 
Các tính chất: 
Tính chất 1: Nếu hàm f tăng (hoặc giảm) trên khoảng (a;b) thì phương trình f(x)=k (k∈R) có không quá một nghiệm 
trong khoảng (a;b). 
Tính chất 2: Nếu hàm f tăng (hoặc giảm) trên khoảng (a;b) thì ∀u, v ∈(a,b) ta có ( )( )f u f v u v= ⇔ = . 
Tính chất 3: Nếu hàm f tăng và g là hàm hằng hoặc giảm trong khoảng (a;b) thì phương trình f(x)=g(x) có nhiều 
nhất một nghiệm thuộc khoảng (a;b). 
Định lý Lagrange: Cho hàm số F(x) liên tục trên đoạn [a;b] và tồn tại F'(x) trên khoảng (a;b) thì 
( )bac ;∈∃ : ( ) ( ) ( )
ab
aFbF
cF
−
−
=' . Khi áp dụng giải phương trình nếu có F(b) – F(a) = 0 thì 
( ) ( ) ( ); : ' 0 ' 0c a b F c F x∃ ∈ = ⇔ = có nghiệm thuộc (a;b). 
Định lý Rôn: Nếu hàm số y=f(x) lồi hoặc lõm trên miền D thì phương trình f(x)=0 sẽ không có quá hai nghiệm 
thuộc D. 
Ví dụ 1: Giải phương trình: 2log2.3 3xx + = . 
Hướng dẫn: 2 2log log2.3 3 2.3 3x xx x+ = ⇔ = − , vế trái là hàm đồng biến, vế phải là hàm nghịch biến nên phương trình 
có nghiệm duy nhất x=1. 
IV. Một số bài toán (đặc biệt là các bài logarrit) ta thường phải đưa về phương trình – hệ phương trình – bất 
phương trình mũ rồi sử dụng các phương pháp trên. 
1.Dạng 1: Khác cơ số: 
Ví dụ: Giải phương trình 7 3log log ( 2)x x= + . Đặt t = 7log 7tx x⇒ = Khi đó phương trình trở thành: 
3
7 1log ( 7 2) 3 7 2 1 2.
3 3
t t
t t tt
   
= + ⇔ = + ⇔ = +   
  
. 
2.Dạng 2: Khác cơ số và biểu thức trong dấu log phức tạp 
Ví dụ 1: Giải phương trình ( )4 2 256log ( 2 2) 2 log 2 3x x x x− − = − − . 
Đặt t = x2 – 2x – 3 ta có ( )6 5log 1 logt t+ = . 
Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 4
Ví dụ 2: Giải phương trình ( )6log2 6log 3 logxx x+ = . Đặt 6logt x= , phương trình tương đương 
36 3 2 3 1
2
t
t t t t  + = ⇔ + = 
 
. 
3. Dạng 3: ( )logb x ca x+ = ( Điều kiện: b = a + c ) 
Ví dụ 1: Giải phương trình ( )7log 34 x x+ = . Đặt ( )7log 3 7 3tt x x= + ⇒ = + , phương trình tương đương 
4 14 7 3 3. 1
7 7
t t
t t    
= − ⇔ + =   
   
. 
Ví dụ 2: Giải phương trình ( ) 42 5log3 +=+ xx . Đặt t = x+4 phương trình tương đương ( ) tt =+1log32 
Ví dụ 3: Giải phương trình ( ) ( ) ( )3 3log 1 log 14 1 2 0x xx x+ +− − − = . 
4. Dạng 4: ( )logax b ss c dx e xα β+ = + + + , với ,d ac e bcα β= + = + 
Phương pháp: Đặt log ( )say b dx e+ = + rồi chuyển về hệ hai phương trình, lấy phương trình hai trừ phương trình 
một ta được: ax b ay bs acx s acy+ ++ = + . Xét ( ) at bf t s act+= + . 
Ví dụ: Giải phương trình 1 77 6log (6 5) 1x x− = − + . Đặt ( )71 log 6 5y x− = − . Khi đó chuyển thành hệ 
( )
( )
1 1
1 1
1
7
7 6 1 1 7 6 5
7 6 7 6
1 log 6 5 7 6 5
x x
x y
y
y y
x y
y x x
−
−
− −
−
 = − + = − 
⇔ ⇒ + = + 
− = − = − 
. Xét hàm số ( ) 17 6tf t t−= + suy ra x=y, Khi đó: 
17 6 5 0x x− − + = . Xét hàm số ( ) 567 1 +−= − xxg x Áp dụng định lý Rôn và nhẩm nghiệm ta được 2 nghiệm của 
phương trình là: x = 1, x = 2. 
5. Dạng 5: Đặt ẩn phụ chuyển thành hệ phương trình. 
Ví dụ: Giải phương trình 1 1 1
8 2 18
2 1 2 2 2 2 2
x
x x x x− − −
+ =
+ + + +
HD: Viết phương trình dưới dạng 1 1 1 1
8 1 18
2 1 2 2 2 2 2x x x x− − − −
+ =
+ + + +
, đặt 1 12 1, 2 1. , 0x xu v u v− −= + = + > . 
 Nhận xét: u.v = u + v. Từ đó ta có hệ: 
8 1 18
.
u v u v
u v u v

+ =
+
 = +
Bµi tËp 
 I Gi¶i c¸c ph−¬ng tr×nh mò 
 1) 13 86
2
=
+− xx ⇒x =2 vµ x=4. 
 2) xx −− = )
2
25,0(4.125,0 82 ⇒x =
3
38
 3) 52x-1+5x+1 - 250 = 0 ⇒x =2 
 4) 9x + 6x = 2.4x ⇒x =0 
 5) 4364 255 −− = xx ⇒x =7/5 
 6) 2243 93 −− = xx ⇒x = ? 
 7) 22x-3 - 3.2x-2 + 1 = 0 ⇒x =1 vµ x=2 
 8) 2442 )
2
5()
5
2( −− = xx ⇒x =1 
 9) 033.43 24 =+− xx ⇒x =0 vµ x=
4
1
Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 5
 10) 52x - 7x - 52x.35 + 7x.35 = 0 ⇒x =
2
1
− 
 11) 
4
410
2
9 2
2
x
x
+
=
−
 ⇒x =3 
 12) 33,0.2
100
32
+= x
x
x
 ⇒x =
13lg
3lg
−
 13) xx 1001,0.1000 = ⇒x =1 vµ x=
2
1
 14) 73 31 3 13 82 − −− − = x xx x ⇒x ∈Φ 
 15) 2x.5x=0,1(10x-1)5 ⇒x =
2
3
 16) 363.2 =xx ⇒x =4 
 17) 42
1)1(
39 =
−−xx
 ⇒x =
2
3
 vµ x=
2
1
− 
 18) 431 )
3
4(
2
1
3
4
.)
4
3( −− = xx ⇒x =2 
 19) 3x+3x+1+3x+2=5x+5x+1+5x+2 ⇒x =
43
31log
5
3 
 20) 2x+2x-1+2x-2=7x+7x-1+7x-2 ⇒x =
343
228log
7
2 
 21) 
44 xx xx = ⇒x =1 vµ x= 3 256 
 22) 161 42.2 ++ = xx ⇒x =
2
1
 23) 4)32()32( =++− xx ⇒x =? 
 24) 10)625()625( =++− xx ⇒x =2 vµ x=-2 
 23) xxx )22()154()154( =++− ⇒x =2 
 24) xxx )5()23()23( =++− ⇒x =? HvQHQTÕ:1997 
 25) 32)125(7)215( +=++− xxx ⇒x =0 vµ x= 7log
2
215+ §HQGHN: D
1997 
 26) 2)625()625( sinsin =−++ xx ⇒x= Πk víi: Zk ∈ §HcÇn th¬: D2000 
 27) 2653 +=+ xxx ⇒x=0 vµ x=1 §HSPHN: A2002 
 28) 21 )1(22 2 −=− −− xxxx ⇒x=1 §Hthuûlîi: A2002 
 29) 093.613.73.5 1112 =+−+− +−− xxxx ⇒x=
5
3log3 ;x= 5log3− §HHång ®øc: A2002 
 30) 112 323 −− += xx ⇒x=? §HDL ®«ng ®«: A-D 
 31) 11 34
2
=−
+− xx
x ⇒x=0;x=2;x=3 C§sp ®ång nai: 2002 
 32) xxx 6242.33.8 +=+ ⇒x=1 vµ x=3 §HQGHN: D2001 
 33) x
x
231 2 =+ ⇒x=2 §Hth¸i Nghuyªn: D2001 
 34) 022.92 2212
22
=+− +++ xxxx ⇒x=-1;x=2 §Hthuû lîi c¬ së II: 2000 
Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 6
 35) 8444)24(2 22
1
−−+=−−+ xxxxx ⇒x=1/2 §Hmë HN: D2001 
 36) 4x2+ x.3x + 3x+1 =2x2.3x + 2x + 6 ⇒x=-1;x=3/2; 3
31; ; log 2
2
 
∈ − 
 
 37) 4sinx-21+sinx.cosxy+
y2 =0 ⇒x=kΠ ;y=o vµ k∈Z 
 38) 
11
2
19
−++
−
=
xx
x ⇒x= 2log3± 
 39) 1
2
12
33
12.623 =+
−
−−
x
xx
x
 ⇒x=1 §HyHN: 2001 
 40) 12122 112 +=−− +++ xxx ⇒x∈ { } [ )∞−∪− ;13 
 41) 1)1( 342 =+ +− xxx ⇒x∈ { }3;1;0 
 42) 1313)1(3)4( 111 ++−+=−+ +−− xxx xxx ⇒x∈ { } [ ]1;01 ∪− 
 43) xx xx = ⇒x=1 vµ x=4 
 44) 232 14231 =+ +−−+ yxyx ⇒x=0,5 vµ y=0,5 
 45) 2 2 4 2 13 3 6 7 1 2.3x xx x+ ++ − + = + ⇒x=-1 
 46) 
)32(10
101)32()32( 1212 22
−
=−++ −−+− xxxx ⇒x=
)32lg(
)32(10lg1
+
+± 
Bài 2: Giải và biện luận phương trình: 
a . ( )2 .2 .2 0x xm m m−− + + = . b . .3 .3 8x xm m −+ = . 
Bài 3: Tìm m sao cho phương trình sau có nghiệm: ( 4).9 2( 2).3 1 0x xm m m− − − + − = . 
II: Giải các phương trình logarit 
1) 3loglog29log 222 3. xxx x −= ⇒x=2 
2) xx 32 log)1(log =+ ⇒x=9 
3) lg(x2-x-6) + x =lg(x+2) + 4 ⇒x=4 
4) )2(log2)2(log5log)1(log
25
15
5
1
2
5 −−+=++ xxx ⇒x= 21 /2 
5) 016)1(log)1(4)1(log)2( 323 =−+++++ xxxx ⇒x=2, x= 81
80
− . 
6) 5,1lg)1(log =+xx ⇒x Φ∈ 
7) 
2
1)213(log 23 =+−−+ xxx ⇒x 2
53 +−
= vµ x =
2
299 −
8) xx −=− 3)29(log2 ⇒x=0 vµ x =3 
9) x
x
x
x
2
3
323 log2
1
3
loglog3log +=− ⇒x=1 vµ x =
8
3
10) log2x + 2log7x = 2 + log2xlog7x ⇒x=7 vµ x = 4 
11) 2log)2(log 22 =++ + xx xx ⇒x=2 §HNNghiÖp I: B2002 
12) )32(log)44(log 1
2
12 −−=+
+xx x ⇒x=2 §HC§oµn: 2002 
13) 4)21236(log)4129(log 232273 =+++++ ++ xxxx xx ⇒x= -1/4 §HKTQD: 2002 
Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 7
14) )1(log2
2log
1)13(log 2
3
2 ++=+−
+
xx
x
 ⇒x=1 §HAn Ninh: 2002 
15) 1)69(loglog 3 =−xx ⇒x Φ∈ §HDL§«ng §«: 2002 
40) 13)23.49(log 13 +=−−+ xxx ⇒x=0 vµ x= 1)153(log3 −+ §HDLPh−¬ng §«ng: 2002 
41) 
2
22 4log6log ... 2)23(log
xy
yx
y
x
 ⇒ (5;5) 
 8) 



=−
=+
1loglog
272
33
loglog 33
xy
yx xy
 ⇒ (3;9) & (
9
1
;
3
1
) 
 9) 






+=+
+=+
3
2loglog12log
2
3loglog3log
333
222
yyxx
xyyx
 ⇒ (1;2) §H Thuû lîi: 2001 
 10) 



=−
=+
1loglog
4
44
loglog 88
yx
yx xy
 ⇒ (8;2) & (
2
1
;
8
1
) §H Tµi chÝnh: 2001 
 11) 



=
=+
8
5)log(log2
xy
yx xy
 ⇒ (4;2) & (2;4) §H DL hïng v−¬ng: 2001 
 12) 





−=+−+−+
+=+−+
1log)4224(log)1(log
)3(log12log)(log
4
2
44
44
22
4
y
x
xyyxy
yxxyx
 ⇒ (2;1) vµ (a;a) víi a *+∈ R §H Má:1999 
 13) 




=+
+−=−
1
)1)(log(log
22
22
yx
xyxyee yx
 ⇒ (
2
2
;
2
2
) §H Th¸i nguyªn: A-B1997 
 14) 



=+−
=−
045
0loglog
22
24
yx
yx
 ⇒ (1;1) vµ (4;2) 
Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 9
 15) 





=−
=−
6
7loglog
2)(log
4 yx
yx
x
x
 ⇒ (5;2) 
 16) 




=+−−
=+
5,0)213(log
7,1lg)1(log
2
3 xx
xx
 ⇒ (
2
53 +−
;
2
299 −
) 
 17) 




=−
=+
1lg3
3lg2
2 xy
xy
 ⇒ ( 10 ;4) 
 18) 



=
=
19log
0logloglog 2
y
xx y
 ⇒x=? 
 19) 



=+
=
+ 3)23(log
2log
1 y
y
x
x ⇒ (2;4) 
 20) 



=−−+
=−
1)(log)(log
2
32
22
yxyx
yx
 ⇒x=? 
 21) 



=−−+
=−
1)3(log)3(log
39
33
22
yxyx
yx
V .Giải bất phương trình mò 
Bµi 1: Gi¶i c¸c bÊtph−¬ng tr×nh sau 
 1) xxx 3413154 )
2
1()
2
1( 2 −+− < ⇒ x =? 
 2) 22x-1 + 22x-3 - 22x-5 >27-x + 25-x - 23-x ⇒ x>8/3 
 3) 8433
131
>+
+
xx ⇒ 0<x<1 
 4) 62.3.23.34 212 ++<++ + xxxx xxx ⇒ x =? 
 5) 1
1
1 )25()25( +
−
−
−≥+ x
x
x ⇒ x ≥1 
 6) 0
12
1221 ≤
−
+−−
x
x
x
 7) 7x+7x+1+7x+2=5x+5x+1+5x+2 
 8) 1)1( 22 2 ≤+− + xxxx 
 9) xxxxxx 21212
222
15.34925 +−++−++− ≥+ 
 10) 12
2
<
−−xx
x 
 11) 1
1
1 )25()25( +
−
−
−≥+ x
x
x 
 12) 623..233.4 212 ++<++ + xxxx xxx 
 13) xxxxxxxx x 3.4352.3.22352 222 +−−>+−− 
 14) 12)
3
1(3)
3
1(
112
>+
+
xx 
Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 10 
 15) xxxx ++ +≤ 142.34 
 16) xxxx 433.54 5,0125,0 −>− −−+ 
 17) (x2+x+1)x<1 
Bài 2: Giải bất phương trình sau: 
12 1 2 0
2 1
x x
x
− + − ≤
−
. 
Bài 3: Cho bất phương trình ( )14 . 2 1 0x xm− − + > a. Giải bất phương trình khi m= 169 . 
 b. Định m để bất phương trình thỏa x R∀ ∈ . 
Bài 4: a. Giải bất phương trình : 
2 1 21 19. 12
3 3
x x
+
   
+ >   
   
 (*) 
 b. Định m để mọi nghiệm của (*) đều là nghiệm của bất phương trình: ( )22 2 2 3 0x m x m+ + + − < 
VI .Giải bất phương trình logarit 
Bài 1: Giải bất phương trình: 
a. ( )28log 4 3 1x x− + ≤ b. 3 3log log 3 0x x− − < 
c. ( )21 4
3
log log 5 0x − >
  
 d. ( ) ( )21 5
5
log 6 8 2 log 4 0x x x− + + − < 
e. 1
3
5log log 3
2 x
x + ≥ f. ( )9log log 3 9 1xx  − <   
g. 2 2log 2.log 2.log 4 1x x x > h. 1
3
4 6log 0x
x
+ ≥ 
i. ( ) ( )2 2log 3 1 log 1x x+ ≥ + − j. 8 1
8
22 log ( 2) log ( 3)
3
x x− + − > 
k. 3 1
2
log log 0x
 
  ≥
 
 
 l. 5log 3 4.log 5 1xx + > 
m. 
2
3 2
4 3
log 0
5
x x
x x
− +
≥
+ −
 n. 1 3
2
log log 1x x+ >
o. ( )22log 5 6 1x x x− + 
q. 
2
2
3
1
5log 1 0
2x
x
x x
+
 
− + ≥ 
 
 r. 6 2
3
1log log 0
2x
x
x
+
− 
> + 
Bài 2) )2(log3log6log
3
1
3
1
2
3 +>−+−− xxxx ⇒x =? 
 Bài 3) 2)22(log)12(log 1
2
12 −>−−
+xx ⇒x ( )3log;5log2 22+−∈ 
 Bài 4 ) )3(log53loglog 242
2
1
2
2 −>−+ xxx ⇒x ( )16;82
1
;0 ∪




∈ 
Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 11 
Bài 5) 32log2log xx xx ≤ ⇒x [ )∞∪





∈ ;2
2
1
;0
3
Bài 6) 3)5(log
)35(log 3
≥
−
−
x
x
a
a víi: 0<a 1≠ ⇒x [ ]3;2∈ 
 Bài 7) )1(loglog)1(loglog 2
5
13
2
5
2
1 xxxx −+>++ ⇒x 





∞−∈
5
12
; 
 Bài 8) log2xlog32x + log3xlog23x o≥ ⇒x [ )∞∪






∈ ;1
6
6
;0 
 Bài 9) 
x
xxx
x x
3
35
5 log
)log2(log
3
loglog −<+ ⇒x ( )3;1
5
5
;0 ∪






∈ 
 Bài 10) 22
2
2
432 655log)(log65 xxxxxxxxxx −+++−>−++ ⇒x 




∈ 3;
2
5
 11) 0
352
)114(log)114(log
2
32
11
22
5 ≥
−−
−−−+−
xx
xxxx
 ⇒x ( )152;2 −−∈ 
 Bài 12) )112(logloglog2 3329 −+> xxx ⇒x ( )4;1∈ 
Bài 13) 0
132
5
5lg
<
+−
−
+
x
x
x
x
 ⇒x ( ) ( )3;10;5 ∪−∈ 
Bài 14: Cho bất phương trình: ( ) ( )2 2log 2 log 2 3a ax x x x− − > − + + thỏa mãn với: 94x = . Giải bất phương trình. 
Bài 15: Tìm m để hệ bất phương trình sau có nghiệm: 
2lg lg 3 0
1
x m x m
x

− + + ≤

>
. 
Bài 16: Cho bất phương trình: ( ) ( )2 1
2
3 3 logx m x m x m x− + + < − 
a. Giải bất phương trình khi m = 2. 
b. Giải và biện luân bất phương trình. 
Bài 17: Giải và biện luân bất phương trình: ( ) ( )log 1 8 2 1xa a x−− ≥ − 
VII. Gi¶i hÖ bÊt ph−¬ng tr×nh mò 
Gi¶i c¸c hÖ bÊt ph−¬ng tr×nh sau : 
1 .
2 22 1 2 2
2
2 9.2 2 0
2 5 4 3
x x x x
x x x
+ + +
− + =

− < − + −
 §S x=2 ; 2)
( ) ( )2 23 4
2
42 3 2 3
2 3
35
121
x x
x
x
x
− −
+ + − ≤
−

 + >

−
 §S 
5 2
3
x< ≤ 
3 
2 1 2 1
1 2 2
2 2
2 1
x y
x y
x y xy
x y
− −
+ +
 + + ≥ +

≥ + +
§S 
1
2
x y= = ; 4) ( )
2
22 2
3
2 2 2 1
log 2 2 0
x y
x y

− = −

− ≤
 §S 
( )
2
2
3log
2
0 1
1 2
y
y
x y
 ≠

≤ ≤

= ± − +

Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 12 
 5) 2 2 1
2
x y
x y
 + ≤

+ ≥ −
 6) 4 4 1
1
x y
x y
 + ≤

+ ≥ −
VIII .Gi¶i hÖ bÊt ph−¬ng tr×nh logarit 
Bµi 1: Gi¶i hÖ bÊt ph−¬ng tr×nh: 
 a. 
2
2
x 4
0
x 16x 64
lg x 7 lg(x 5) 2lg2
 +
>
− +
 + > − −
 b. 
( ) ( ) ( )
( )
x 1 x
x
x 1 lg2 lg 2 1 lg 7.2 12
log x 2 2
+
− + + < +

+ >
 c. 
( )
( )
2 x
4 y
log 2 y 0
log 2x 2 0
−
−
 − >

− >
 d 
( )
( )

>+
+<++− +
22log
)122.7lg()12lg(2lg1 1
x
x
x
xx
 IX .Gi¶i c¸c ph−¬ng tr×nh (cã ®iÒu kiÖn) sau: 
 1) T×m gÝa trÞ Min cña hµm sè: y= )1(log)3(log 2321 22 ++− −+ xx xx . 
 2) T×m tÊt c¶ c¸c nghiÖm cña ph−¬ng tr×nh: (2 xx =− 2)1 . 
 *) Thuéc miÒn x¸c ®Þnh cña hµm sè: y= lg(4x-1) ⇒x=1 
 *) Thuéc miÒn x¸c ®Þnh cña hµm sè: y= ln(x2- x-2) ⇒x=-5/3 
 3) Gi¶i: logaaxlogxax=
aa
1log 2 víi: 0<a≠ 1 ⇒x=1/a2 vµ x=
a
1
 4) X¸c ®Þnh m ®Ó ph−¬ng tr×nh: 0)22(log2)32(log4
2
1
22
2
2
=+−++− +−−− mxxx xxmx 
 cã ba nghiÖm? ⇒m=1/2 , m =3/2 vµ m=1 
 5) §Þnh m ®Ó ph−¬ng tr×nh: 0)122(log)4(log
3
1
2
3 =−−++ mxmxx cã nghiÖm duy nhÊt? 
 ⇒m=0 , ≤−
2
1
 m
10
1−≤ 
 6) §Þnh m ®Ó ph−¬ng tr×nh: 2)1(log
log
5
5
=
+x
mx
 cã nghiÖm duy nhÊt? ⇒m=? 
 7) T×m x ®Ó: )13(log)65(log 2222322 −−=−+− + xxxmxm m ®−îc nghiÖm ®óng víi mäi m? 
⇒x=5. 
 8) T×m x ®Ó: )15(log)535(log 22222 −−=−++− + xxmxxm m ®óng víi ∀m⇒x=? 
§HYHphßng:2001 
 9) T×m m ®Ó ph−¬ng tr×nh: lg(x2+mx) – lg(x-3) = 0 cã nghiÖm? 
10) Víi gi¸ trÞ nµo cña x th×: 
2lg
1lg 2
2
+
+=
x
xy ®¹t gi¸ trÞ nhá nhÊt? 
Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 13 
11) Cho hµm sè: )2(log
)1(
+−
−+
=
mmx
mxm
y
a
 víi: 0<a 1≠ 
 a) T×m miÒn x¸c ®Þnh cña hµm sè khi m=
2
1
− 
 b) T×m tÊt c¶ c¸c gi¸ trÞ cña m ®Ó hµm sè x¸c ®Þnh víi 1≥∀x . 
12) T×m m ®Ó c¸c nghiÖm x1,x2 cña : 0)2(log)422(log2 22
2
1
22
4 =−++−+− mmxxmmxx tho¶: 
122
2
1 >+ xx 
13) T×m tÊt c¶ c¸c gi¸ trÞ cña m ®Ó: 01)2(log)5()2(log)1(
2
1
2
2
1 =−+−−−−− mxmxm 
 cã 2 nghiÖm tho¶ mkn: 2<x1 ≤x2<4. 
14) T×m m ®Ó ph−¬ng tr×nh: )3(log3loglog 242
2
1
2
2 −=−+ xmxx cã nghiÖm thuéc [ )+∞;32 
15) Gi¶i vµ biÖn luËn ph−¬ng tr×nh: 4)2(log 2
2 2
=+
−
mx
x
 tuú theo m R∈ . 
16) Gi¶i vµ biÖn luËn : 
)
2
1(log)2(log)
2
1(log])13(1[)2(log])2(1[
2
11
2
3
2
11
22
3
2 xxx
x
mxxm −+−=−−++−++ 
17) Gi¶i vµ biÖn luËn ph−¬ng tr×nh: 2lgx - lg(x-1) = lga víi a∈R. 
18) Gi¶i vµ biÖn luËn ph−¬ng tr×nh: 2x2 +(1- log3m)x+ log3m – 1 = 0 víi m
*
+∈ R 
19) Gi¶i vµ biÖn luËn ph−¬ng tr×nh: 0logloglog 2 =++ aaa
xaaxx
 víi a *+∈ R 
20) T×m m ®Ó: 0log)1(log 25225 =++++ −+ xmmxx cã nghiÖm duy nhÊt? 
21) T×m m ®Ó: 0)(log)4(log 2
7
17 =−++− xmxxm cã ®óng hai nghiÖm ph©n biÖt? 
22) Cho ph−¬ng tr×nh: 04)1lg()1(2)1(lg)1( 22222 =+++−−+− mxxmxx 
 a) Gi¶i ph−¬ng tr×nh khi: m=-4 
 b) T×m m ®Ó ph−¬ng tr×nh cã ®óng hai nghiÖm tho¶: 31 ≤≤ x 
23) T×m a ®Ó: xaxx aa log)3(log 2 =−+ cã nghiÖm? 
24) T×m a ®Ó: log2(2
x+1).log2(2
x+1+2)=2+a cã nghiÖm? 
25) T×m a ®Ó: )2(log)2(log 22
2
2
++
=+++
xx
a
axx 
X Gi¶i c¸c bÊt ph−¬ng tr×nh (cã ®iÒu kiÖn) sau: 
1) Trong c¸c nghiÖm cña: 1)(log 22 ≥++ yxyx Hky t×m nghiÖm cã tæng: x+2y lín nhÊt? 
 2) Chøng minh r»ng: 
2
log2loglog 222
baba +≤+ Víi: a,b ≥ 1 
 3) T×m nghiÖm cña: 32sin
2
1
sin3 2 ≥+ xx Tho¶ mkn: lg(x2+x+1)<1 
 4) Gi¶i: loga(x
2-x-2)>loga(-x
2+2x+3) biÕt nã cã mét nghiÖm x=9/4. 
 5) Cho 03log)6(log)15(log 2521 ≥++++++ a
a
axxaxx .T×m a ®Ó bpt cã nghiÖm duy nhÊt? t×m 
nghiÖm ®ã? 
 6) Víi gi¸ trÞ nµo cña a th× bpt: log2a+1(2x-1)+loga(x+3)>0. §−îc tho¶ mkn ®ång thêi t¹i x=1 vµ x=4. 
Lê Lợi 
C¸c b¹n cè g¾ng lªn nhÐ ! ↑ 14 
 7) Gi¶i vµ biÖn luËn theo a: logxa + logax + 2cosa 0≤ 
 8) Cho hai bÊt ph−¬ng tr×nh: logx(5x
2-8x+3)>2 (1) vµ x2 - 2x + 1 - a4 0≥ (2). 
 X¸c ®Þnh a sao cho: Mäi nghiÖm cña (1) còng lµ nghiÖm cña (2) ? 
 9) Gi¶i vµ biÖn luËn bÊt ph−¬ng tr×nh: logx100 - 2
1
logm100 > 0. 
10) Víi gi¸ trÞ nµo cña m th× bpt: 3)2(log 2
2
1 −>+− mxx cã nghiÖm vµ mäi nghiÖm cña nã ®Òu thuéc 
miÒn 
 x¸c ®Þnh cña hµm sè: 2log)1(log 13 −+= + xxy xx 
11) Gi¶i vµ biÖn luËn: xax xa 21log >+ 
12) Cho: xmxmxmx
2
1
2 log)(3)3( −<++− (1). 
 a) KiÓm nghiÖm r»ng víi m=2 th× bÊt ph−¬ng tr×nh kh«ng cã nghiÖm? 
 b) Gi¶i vµ biÖn luËn (1) theo m! 
13) Cho 3)5(log
)35(log 3
>
−
−
x
x
a
a (1). Víi: 0<a≠ 1 vµ 1+log5(x
2+1)-log5(x
2+4x+m)>0 (2). 
 T×m tÊt c¶ c¸c gi¸ trÞ cña m sao cho mäi nghiÖm cña (1) ®Òu lµ nghiÖm cñ (2)? 
14) T×m c¸c gi¸ trÞ x tho¶: x>1 nghiÖm ®óng bpt: 
 1)1(log 22 2 <−++ mx
m
xx
 Víi: .40 ≤3 §HGTVT¶i: 2002 
15) Gi¶i vµ biÖn luËn: 2log
2
1loglogloglog 22 aaaaa xx ≥+ ⇒x=? §HNNI: A
2002 
16) Gi¶i vµ biÖn luËn: 1)1(log 2
2
1 <++ axx ⇒x=? §HTh¨ng long: A
2002 
17) T×m m sao cho: logm(x
2-2x+m+1)>0. §óng víi mäi x. ⇒x=? §H®µ n½ng: A2002 
18) T×m m ®Ó: 02)5(log6)5(log3)5(log
25
155
5
1 ≤+−+−+− xxx vµ: 0)35)(( ≥−− xmx 
 chØ cã 1 nghiÖm chung duy nhÊt? ⇒x=? ViÖn §HMëHN: A2002 
19) T×m m ®Ó [ ]2;0∈∀x ®Òu tho¶: 5)2(log2log 2422 ≤+−++− mxxmxx ⇒x=? §HspHN: A2001 
20) Cho bÊt ph−¬ng tr×nh: xax 22 loglog >+ 
 a) gi¶i khi a=1? ⇒x 








∈
+
2
51
2;
2
1
 b) X¸c ®Þnh a ®Ó bpt cã nghiÖm? ⇒ a
4
1
−≥ HViÖn BCVT: A2002 
21) §Þnh m ®Ó: logx-m(x
2-1)>logx-m(x
2+x-2) cã nghiÖm? ⇒x =? §H®µ l¹t: A-B2002 
22) T×m m ®Ó: 0)
1
log1(2)
1
log1(2)
1
log2( 2222 ≥
+
+−
+
++
+
−
m
m
m
m
x
m
m
x cã nghiÖm duy nhÊt? 
⇒m=
31
32
− 
23) T×m m ®Ó: xmxmxmx
2
1
2 log)(3)3( −≤++− cã nghiÖm duy nhÊt? t×m nghiÖm ®ã? ⇒m=2. 
24) §Þnh m ®Ó: xxx m
222 sincossin 3.32 ≥+ cã nghiÖm? ⇒x =? §HQGHN: 1999