Một số công thức Toán cần nhớ

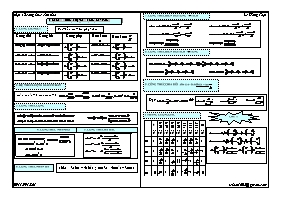
7. CÔNG THỨC BIẾN ĐỔI TỔNG è TÍCH
I. CÔNG THỨC LƯỢNG GIÁC CƠ BẢN
Cos – đối ; sin – bù ; phụ - chéo
1. CUNG LIÊN KẾT
Cung đối
Cung bù
Cung phụ
Hơn kém p
Hơn kém 
5. CÔNG THỨC BIẾN ĐỔI TỔNG -> TÍCH
8. CÔNG THỨC BIẾN ĐỔI TÍCH è TỔNG
9. CÔNG THỨC CHIA ĐÔI .sin – cos – tan theo t = tan
2. HỆ THỨC LƯỢNG GIÁC CƠ BẢN
sin2a+cos2a = 1; tana.cota = 1;	
Đặt: thì: ; ;	 
3. CÔNG THỨC CỘNG
CHÚ Ý
10. BẢNG LƯỢNG GIÁC
; 
0
00
300
450
600
900
1200
1350
1500
1800
sin
0
1
0
cos
1
0
–1
tan
0
1
–1
0
cot
1
0
–1
; 
4. CÔNG THỨC NHÂN ĐÔI 5. CÔNG THỨC HẠ BẠC
; 
6. CÔNG THỨC NHÂN BA 
sin3a = 3sina – 4sin3a ; cos3a = 4cos3a – 3cosa
5.	Một số điều cần lưu ý khi giải phương trình:
	a/	Khi khi giải các phương trình có chứa các hàm tan, cot, có mẫu hoặc chứa căn bậc chẵn, thì phải đặt ĐIỀU KIỆN để phương trình xác định:
*	Phương trình chứa tanx đk : 
*	Phương trình chứa cotx đk : 
*	Phương trình chứa cả tanx và cotx đk :
	b/	Khi tìm được nghiệm phải kiểm tra điều kiện. thường dùng một trong các cách sau:
1.Kiểm tra trực tiếp bằng cách thay x vào biểu thức điều kiện.
2.Dùng đường tròn lượng giác.
II. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
1.	PHƯƠNG TRÌNH sinx = sina
a/
b/ 
c/ 
d/
Trường hợp đặc biệt:
2.	PHƯƠNG TRÌNH cosx = cosa
a/
b/ 
c/
d/
Trường hợp đặc biệt:
3.	PHƯƠNG TRÌNH tanx = tana
a/
b/
c/
d/ 
Trường hợp đặc biệt:
4.	PHƯƠNG TRÌNH cotx = cota
a/
b/
CÔNG THỨC MŨ: y = ax ( 0< a 1)
CÔNG THỨC LOGARIT : y =logax (x>0; 0<a1)
CÔNG THỨC ĐẠO HÀM
S
-S
C
-C
Hàm số sơ cấp
Hàm số hợp
CÔNG THỨC NGUYÊN HÀM
 BẤT PHƯƠNG TRÌNH MŨ
BẤT PHƯƠNG TRÌNH LOGARIT
ð 0 av u < v.
ð a > 1	: au > av u > v.
Bpt
Đk
Tập nghiệm
a>1
0< a < 1
ax> b
b 0
R
R
b > 0
x > logab
x < logab
ax< b
b 0
b > 0
x < logab
x > logab
ð a >1: logaf(x) >logag(x) f(x) >g(x) >0
ð 0logag(x)0<f(x)<g(x).
ð logaf(x) ³ logag(x)Û 
Bpt
Tập nghiệm
a > 1
0< a < 1
loga x > b
x > ab
0 < x < ab
loga x < b
0 < x <ab
x > ab