Một số cách tính thể tích khối tứ diện gần đều

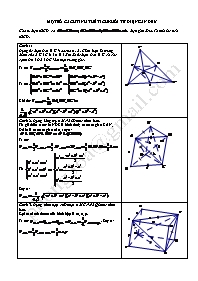
MỘT SỐ CÁCH TÍNH THỂ TÍCH KHỐI TỨ DIỆN GẦN ĐỀU
Cho tứ diện ABCD có (tứ diện gần đều). Ta tính thể tích ABCD.
Cách 1: 
Dựng tứ diện D.A’B’C’ sao cho A, B, C lần lượt là trung điểm của B’C’, C’A’, A’B’. Khi đó tứ diện D. A’B’C có các cạnh DA’, DB’, DC’ đôi một vuông góc.
Ta có 
Ta có 
Khi đó: 
Cách 2: Dựng lăng trụ AMNBCD như hình bên. 
Từ giả thiết ta có: MNDC là hình thoi; các tam giác CAN, DAM là các tam giác cân, suy ra: 
Ta có: 
Từ 
Suy ra:
Cách 3: Dựng hình hộp chữ nhật AMCN.PBQD như hình bên. 
Gọi các kích thước của hình hộp là m, n, p. 
Ta có: . Suy ra: 
Ta có: 
Cách 4: Sử dụng công thức 
Gọi I, J lần lượt là trung điểm của AB và CD. Ta chứng minh được IJ là đường vuông góc chung của AB và CD. Gọi là góc giữa AB và CD.
Ta có 
+ 
+ (*)
Tính (**)
Tương tự: 
Thay vào (**) ta được: 
Từ (*) ta có 
Ta có: 
Cách 5: Gọi I, J, M, N, P, Q lần lượt là trung điểm của AB, CD, AC, BD, AD, BC. 
Ta thấy tứ giác MINJ là hình thoi. Ta chứng minh được PQ vuông góc với AD và BC nên PQ vuông góc với mp(IMJN).
Gọi G là giao điểm của các đường IJ, MN, PQ. 
Ta có 
Vì nên 
Suy ra 
Ta tính được:
Tương tự: 
; 
Từ đó: