Lý thuyết và Bài tập về Số phức

SỐ PHỨC
I – LÝ THUYẾT CHUNG
1. Khái niệm số phức
	· Tập hợp số phức: 	C
	· Số phức (dạng đại số) : 
	(a, b, a là phần thực, b là phần ảo, i là đơn vị ảo, i2 = –1)
	· z là số thực 	Û phần ảo của z bằng 0 (b = 0)
	 z là thuần ảo 	Û phần thực của z bằng 0 (a = 0)
	 Số 0 vừa là số thực vừa là số ảo.
	· Hai số phức bằng nhau: 	
Chú ý: 
O
M(a;b)
y
x
a
b
.
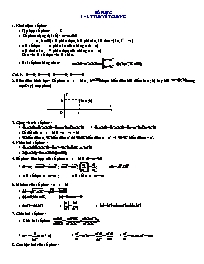
2. Biểu diễn hình học: Số phức z = a + bi (a, b được biểu diễn bởi điểm M(a; b) hay bởi trong mp(Oxy) (mp phức) 
3. Cộng và trừ số phức: 
	· · 
	· Số đối của z = a + bi là –z = –a – bi 
	· biểu diễn z, biểu diễn z' thì biểu diễn z + z’ và biểu diễn z – z’.
4. Nhân hai số phức :
	· 
	· 
5. Số phức liên hợp của số phức z = a + bi là 
 	· ;	
 · z là số thực Û ; 	z là số ảo Û 
6. Môđun của số phức : z = a + bi 
 · 
	· 
	· 	· 	· 
7. Chia hai số phức:
 Chia hai số phức: .
	· (z ¹ 0)	· 	· 
8. Căn bậc hai của số phức: 
	· là căn bậc hai của số phức Û Û 
	· w = 0 có đúng 1 căn bậc hai là z = 0
	· w có đúng hai căn bậc hai đối nhau 
 · Hai căn bậc hai của a > 0 là 
 · Hai căn bậc hai của a < 0 là 
9. Phương trình bậc hai Az2 + Bz + C = 0 (*) (A, B, C là các số phức cho trước, A ).
 · : (*) có hai nghiệm phân biệt , ( là 1 căn bậc hai của D)
 	· : (*) có 1 nghiệm kép: 
	Chú ý: Nếu z0 Î C là một nghiệm của (*) thì cũng là một nghiệm của (*).
10. Dạng lượng giác của số phức (dành cho chương trình nâng cao)
a) Acgumen của số phức z ≠ 0:
	Cho số phức z ≠ 0. Gọi M là điểm biểu diễn số z. Số đo (radian) của mỗi góc lượng giác tia đầu Ox, tia cuối OM được gọi là một acgumen của z. Nếu j là một acgumen của z thì mọi acgumen của z có dạng j + k2p (kÎZ).
b) Dạng lượng giác của số phức :
	Dạng z = r(cosj + isinj) (r > 0) là dạng lượng giác của z = a + bi (a, bÎR) (z ≠ 0)
	Û (j là acgumen của z, j = (Ox, OM).
c) Nhân, chia số phức dưới dạng lượng giác :
Nếu z = r(cosj + isinj), z’ = r’(cosj’ + isinj’) thì:
z.z’ = rr’[cos(j + j’) + isin(j +j’)]
.
d) Công thức Moa-vrơ : 
	Với n là số nguyên, n ³ 1 thì : 
Khi r = 1, ta được : 
e) Căn bậc hai của số phức dưới dạng lượng giác :
	Các căn bậc hai của số phức z = r(cosj + isinj) (r > 0) là : và .
II – CÁC DẠNG BÀI TẬP
PHẦN 1: SỐ PHỨC VÀ CÁC PHÉP TOÁN TRÊN SỐ PHỨC
A – CÁC VÍ DỤ
Ví dụ 1: Cho số phức z = . Tính các số phức sau: ; z2; ()3; 1 + z + z2 
Giải:
Vì z = Þ = 
Ta có z2 = ==
Þ ()2 = 
()3 =()2 . = 
Ta có: 1 + z + z2 = 
Ví dụ 2: Tìm các số thực x, y thoả mãn: 
 3x + y + 5xi = 2y – 1 +(x – y)i
Giải: Theo giả thiết: 3x + y + 5xi = 2y – 1 +(x – y)i
Û (3x + y) + (5x)i = (2y – 1) +(x – y)i
Û Giải hệ này ta được: 
Ví dụ 3: Tính:
 i105 + i23 + i20 – i34
Giải: Để tính toán bài này, ta chú ý đến định nghĩa đơn vị ảo để từ đó suy ra luỹ thừa của đơn vị ảo như sau:
Ta có: i2 = -1; i3 = -i; i4 = i3.i = 1; i5 = i; i6 = -1
Bằng quy nạp dễ dàng chứng minh được: i4n = 1; i4n+1 = i; i4n+2 = -1; i4n+3 = -i; " n Î N*
	Vậy in Î {-1;1;-i;i}, " n Î N.
	Nếu n nguyên âm, in = (i-1)-n = .
	Như vậy theo kết quả trên, ta dễ dàng tính được: 
 i105 + i23 + i20 – i34 = i4.26+1 + i4.5+3 + i4.5 – i4.8+2 = i – i + 1 + 1 = 2
Ví dụ 4: Tính số phức sau: z = 
Giải: Ta có: 
Þ . Vậy =i16 +(-i)8 = 2
Ví dụ 5: Tìm phần ảo của z biết: 
Giải: Giả sử z=a+bi
.
Vậy phần ảo của z bằng -10
Ví dụ 6: Cho Tính 
Giải:
Ví dụ 7: Cho . Tính ; ; 
Giải:
+) 
+) 
+) 
Ví dụ 8: Tìm các căn bậc hai của số phức 
Giải: Giả sử m+ni (m; nR) là căn bậc hai của z
Ta có: 
Thay (2) vào (1) ta có: 
Vậy z có hai căn bậc hai là 3+2i và -3-2i
Ví dụ 9: Tính số phức sau: z = (1+i)15
Giải:
	Ta có: (1 + i)2 = 1 + 2i – 1 = 2i Þ (1 + i)14 = (2i)7 = 128.i7 = -128.i
	z = (1+i)15 = (1+i)14(1+i) = -128i (1+i) = -128 (-1 + i) = 128 – 128i.
C. BÀI TẬP TRẮC NGHIỆM
DẠNG 1: Tìm phần thực, phần ảo của số phức:
Mức độ 1:
Câu 1. Phần ảo của số phức là.
	A. .	B. .	C. .	D. .
Chọn D
Câu 2. Cho số phức . Tìm phần ảo của số phức 
	A. .	B. .	C. .	D. .
Chọn B
Câu 3. Cho số phức thỏa mãn . Tìm phần thực và phần ảo của số phức .
	A. Phần thực bằng , phần ảo bằng .	B. Phần thực bằng , phần ảo bằng .
	C. Phần thực bằng -3, phần ảo bằng .	D. Phần thực bằng , phần ảo bằng .
Chọn B Vì . Do đó số phức có phần thực bằng , phần ảo bằng .
Câu 4. Phần thực và phần ảo của số phức .
	A. và .	B. và .	C. và .	D. và .
Chọn C
Ta có.Vậy phần thực của số phức là và phần ảo là .
Câu 5. Tìm phần ảo của số phức biết .
	A. .	B. .	C. .	D. .
Chọn C
Ta có: .Vậy phần ảo của số phức là .
Câu 6. Điểm trong hình vẽ bên là điểm biểu diễn số phức . Tìm phần thực và phần ảo của số phức .
	A. Phần thực là và phần ảo là .	B. Phần thực là và phần ảo là .
	C. Phần thực là và phần ảo là .	D. Phần thực là và phần ảo là .
Chọn D Điểm biểu diễn số phức . Có phần thực là và phần ảo là .
Câu 7. Cho số phức . Phần ảo của là
	A. .	B. .	C. .	D. .
Chọn B Số phức có phần ảo là .
Câu 8. Cho số phức . Xác định phần thực và phần ảo của số phức .
	A. Phần thực bằng 5 và phần ảo bằng .	B. Phần thực bằng 5 và phần ảo bằng .
	C. Phần thực bằng 5 và phần ảo bằng .	D. Phần thực bằng 5 và phần ảo bằng 7.
Chọn D
Số phức liên hợp của là . Suy ra, phần thực của bằng 5 và phần ảo của bằng 7.
Câu 9. Cho số phức . Tìm phần thực và phần ảo của số phức .
	A. Phần thực bằng và phần ảo bằng .	B. Phần thực bằng và phần ảo bằng .
	C. Phần thực bằng và phần ảo bằng .	D. Phần thực bằng và phần ảo bằng .
Chọn B .Phần thực bằng và phần ảo bằng .
Câu 10. Phần ảo của số phức là
	A. .	B. .	C. .	D. .
Chọn D Số phức có phần thực , phần ảo nên chọn A.
Câu 11: Phần thực và phần ảo của số phức lần lượt là:
A. và 	B. và .	C. và .	D. và .
Chọn C Số phức có phần thực và phần ảo lần lượt là và .
Câu 12: Phần ảo của số phức là
A. .	B. .	C. .	D. .
Chọn C Phần ảo của số phức là .
Câu 13: Xác định phần ảo của số phức .
A. .	B. .	C. .	D. .
Chọn A Phần ảo của số phức là .
Câu 14: Tìm phần ảo của số phức , biết .
A. .	B. .	C. .	D. .
Chọn B Ta có: .
Vậy phần ảo của số phức bằng .
Câu 15: Phần thực của số phức là
A. .	B. .	C. .	D. .
Chọn A Ta có: .
Câu 16: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Số phức có phần thực là , phần ảo là .
B. Số phức có phần thực là , phần ảo là .
C. Số phức có phần thực là , phần ảo là .
D. Số phức có phần thực là , phần ảo là .
Chọn A Mỗi số phức có phần thực là , phần ảo là .
Câu 17: Phần thực và phần ảo của số phức liên hợp của số phức là:
A. Phần thực là , phần ảo là .	B. Phần thực là , phần ảo là .
C. Phần thực là , phần ảo là .	D. Phần thực là , phần ảo là .
Chọn A
Ta có số phức liên hợp của số phức là , suy ra Phần thực và phần ảo của số phức liên hợp của số phức là và .
Câu 18: Cho số phức có số phức liên hợp . Tổng phần thực và phần ảo của số phức bằng.
A. .	B. .	C. .	D. .
Chọn C Ta có: . Vậy tổng phần thực và phần ảo của số phức bằng .
Câu 19: Cho số phức . Hiệu phần thực và phần ảo của bằng.
A. .	B. .	C. .	D. .
Chọn C Phần thực và phần ảo lần lượt là và . Vậy hiệu phần thực và phần ảo của bằng .
Câu 20: Cho số phức . Tìm phần thực của số phức .
A. .	B. .	C. .	D. .
Chọn A Ta có . Vậy phần thực của số phức là .
Câu 21: Số phức nào dưới đây là số thuần ảo ?
A. .	B. .	C. .	D. .
Chọn B 
MỨC ĐỘ 2:
Câu 1: Cho số phức . Số phức có phần ảo là:
A. .	B. .	C. .	D. .
Chọn A Ta có . Vậy số phức có phần ảo là .
Câu 2: Cho hai số phức và . Phần ảo của số phức là
A. .	B. .	C. .	D. .
Chọn C Ta có . Vậy phần ảo của số phức là 12.
Câu 3: Cho số phức . Số phức có phần ảo là
A. .	B. .	C. .	D. .
Chọn A có phần ảo là .
Câu 4. Nghiệm có phần ảo dương của phương trình là
	A. .	B. .	C. .	D. .
Chọn B Ta có .PT có hai nghiệm là và . Ta chọn .
Câu 5: Phần thực và phần ảo của số phức lần lượt là 
A. và .	B. và .	C. và .	D. và .
Chọn B 
Ta có . Vậy phần thực của số phức bằng và phần ảo của số phức bằng .
Câu 6: Tìm phần ảo của số phức biết .
A. .	B. .	C. .	D. .
Chọn D
Ta có: . Vậy phần ảo của số phức là .
Câu 7: Tổng phần thực và phần ảo của số phức là 
A. .	B. .	C. .	D. .
Chọn B 
Ta có 
phần thực , phần ảo .Vậy .
Câu 8: Tìm phần ảo của số phức , biết .
A. 	B. 	C. 	D. 
Chọn C Ta có: Vậy phần ảo của số phức là 
Câu 9. Cho hai số phức: Phần ảo của số phức bằng:
	A. .	B. .	C. .	D. .
Chọn A .
Câu 10. Cho số phức . Số phức có phần thực là:
	A. .	B. .	C. .	D. .
Chọn C . Vậy số phức có phần thực là .
Câu 11. Cho số phức khác . Tìm phần ảo của số phức .
	A. .	B. .	C. .	D. .
Chọn D
Ta có . Vậy phần ảo của là .
Câu 12. Cho số phức thỏa mãn: . Hiệu phần thực và phần ảo của số phức là:
	A. .	B. .	C. .	D. .
Chọn A Ta có .
. Suy ra hiệu phần thực và phần ảo của bằng .
Câu 13. Cho hai số phức , . Tìm phần ảo của số phức .
	A. .	B. .	C. .	D. .
Chọn A ; . Vậy phần ảo của số phức bằng .
Mức độ 3:
Câu 1: Cho số phức thỏa mãn . Tính tích phần thực và phần ảo của số phức .
A. .	B. .	C. .	D. .
Chọn B Gọi (với ), ta có .
Theo giả thiết, ta có 
 . Vậy .
Câu 2: Tìm phần thực, phần ảo của số phức , biết là một căn bậc hai của và có phần thực lớn hơn phần ảo. 
A. Phần thực bằng , phần ảo bằng .	B. Phần thực bằng , phần ảo bằng .
C. Phần thực bằng , phần ảo bằng .	D. Phần thực bằng , phần ảo bằng .
Chọn D 
Gọi . Ta có .
Suy ra .
Do phần thực của lớn hơn phần ảo của nên .
Câu 3: Cho số phức thỏa mãn điều kiện . Tìm phần ảo của số phức .
A. .	B. .	C. .	D. .
Chọn B .
 . Vậy phần ảo của bằng .
Câu 4. Phần thực và phần ảo của số phức lần lượt là:
	A. và .	B. và .	C. và .	D. và .
Chọn B .
Câu 5. Cho hai số phức và , Tìm tập hợp tất cả các giá trị để là số thực.
	A. .	B. .	C. .	D. .
Chọn B Ta có: Để là số thực.
Câu 6. Số phức thỏa mãn có phần thực bằng.
	A. .	B. .	C. .	D. .
Chọn C Ta có: nên số phức có phần thực bằng .
Câu 7. Cho số phức với là tham số thực. Với giá trị nào của thì có phần thực bằng .
	A. .	B. .	C. .	D. .
Chọn C
Cách 1:
Bước 1: Dùng CASIO chuyển sang số phức (mode 2).
Bước 2: Nhập biểu thức: ( Ở đây biến là ).
Bước 3: CALC với là các giá trị trong các phương án, xem số phức nào có phần thực là .
Cách 2:
Viết về dạng: . Giải phương trình .
Câu 8. Cho số phức . Tìm phần thực và phần ảo của số phức ?
	A. Phần thực bằng và phần ảo bằng .	B. Phần thực bằng và phần ảo bằng .
	C. Phần thực bằng và phần ảo bằng .	D. Phần thực bằng và phần ảo bằng .
Chọn C Ta có .
Vậy số phức có phần thực bằng và phần ảo bằng .
Câu 9. Cho số phức . Khi đó phần thực và phần ảo của số phức là.
	A. , .	B. , .
	C. , .	D. , .
Chọn B
Ta có: .
.
DẠNG 2 : SỐ PHỨC LIÊN HỢP
Mức độ 1 :
Câu 1. Số phức liên hợp của số phức là
	A. .	B. .	C. .	D. .
Chọn A Số phức liên hợp của số phức , là số phức . Do đó số phức liên hợp của số phức là .
Câu 2. Số phức liên hợp của số phức là
	A. .	B. .	C. .	D. .
Chọn B
Hai số phức liên hợp có phần thực bằng nhau và phần ảo đối nhau nênsuy ra 
Câu 3. Số phức liên hợp của là
	A. .	B. .	C. .	D. .
Chọn B Số phức liên hợp của là .
Câu 4. Số phức z thỏa mãn là
	A. z = 1 –2i.	B. z = –2 – i.	C. z = 2 + i.	D. z = –2 + i.
Chọn C Ta có: 
Câu 5: Cho số phức . Số phức liên hợp của là
A. .	B. .	C. .	D. .
Chọn D Số phức liên hợp của là .
Câu 6: Số phức liên hợp của số phức là
A. .	B. .	C. .	D. .
Chọn A Số phức liên hợp của số phức là  ...  phức nào dưới đây? 
	A. .	B. .	C. .	D. .
Chọn C Điểm nên nó biểu diễn cho số phức .
Câu 8. Trong mặt phẳng , điểm nào sau đây biểu diễn số phức ?
	A. .	B. .	C. .	D. .
Chọn A Số phức có điểm biểu diễn nên số phức có điểm biểu diễn là .
Câu 9. Điểm biểu diễn cho số phức trong mặt phẳng tọa độ phức là:
	A. .	B. .	C. .	D. .
Chọn D Ta có: Phần thực là và phần ảo là .
Câu 10: Số phức liên hợp của số phức có điểm biểu diễn là điểm nào dưới đây?
A. .	B. .	C. .	D. .
Chọn A Ta có: nên điểm biểu diễn của số phức là .
Câu 11: Điểm trong hình vẽ bên dưới biểu diễn cho số phức . Mệnh đề nào sau đây đúng?
A. Phần thực là , phần ảo là .	B. Phần thực là , phần ảo là .
C. Phần thực là , phần ảo là .	D. Phần thực là , phần ảo là .
Lời giải
Chọn A 
Câu 12: Điểm trong hình bên là điểm biểu diễn cho số phức 
A. .	B. .	C. .	D. .
Chọn B Điểm biểu diễn cho số phức . 
Câu 13: Tìm tọa độ điểm là điểm biểu diễn số phức .
A. .	B. .	C. .	D. .
Chọn A Ta có điểm biểu diễn số phức .
Câu 14: Số phức có điểm biểu diễn trên mặt phẳng tọa độ là . Tìm tọa độ điểm 
A. .	B..	C..	D. .
Chọn A Số phức có điểm biểu diễn trên mặt phẳng tọa độ là.
Câu 15: Điểm M trong hình vẽ dưới đây biểu thị cho số phức 
A. .	B. .
C. .	D. .
Chọn B
Câu 16: Trong mặt phẳng phức, cho số phức . Điểm biểu diễn cho số phức là điểm nào sau đây
A. .	B. .	C. .	D. .
Chọn B Ta có: nên có điểm biểu diễn là .
Câu 17: Trong mặt phẳng , điểm trong hình vẽ bên là điểm biểu diễn số phức . Số phức là
A. .	B. .	C. .	D. .
Chọn C Ta có .
Câu 18: Điểm trong hình vẽ dưới đây biểu diễn số phức .
Số phức bằng
A. .	B. .	C. .	D. .
Chọn A Theo hình vẽ thì . 
Mức độ 2:
Câu 1. Trong mặt phẳng tọa độ cho các điểm , như hình vẽ bên. Trung điểm của đoạn thẳng biểu diễn số phức
	A. .	B. .	C. .	D. .
Chọn C Điểm , . Gọi là trung điểm đoạn thẳng suy ra . Vậy điểm biểu diễn số phức .
Câu 2. Điểm trong hình vẽ bên là điểm biểu diễn của số phức .
Khi đó mệnh đề nào sau đây là đúng?
	A. .	B. .	C. .	D. .
Chọn C Điểm biểu diễn số phức .
Câu 3. Cho số phức . Biểu diễn số phức là điểm:
	A. .	B. .	C. .	D. .
Chọn A Ta có: .
Do đó, điểm biểu diễn số phức là điểm .
Câu 4. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức liên hợp của số phức ?
	A. .	B. .	C. .	D. .
Chọn D Điểm biểu diễn số phức liên hợp của số phức là điểm .
Câu 5: Cho số phức . Điểm nào dưới đây là điểm biểu diễn của số phức trên mặt phẳng toạ độ?
A. .	B. .	C. .	D. .
Chọn A .
Vậy điểm biểu diễn của số phức là .
Câu 6: Điểm biểu diễn của số phức là . Tọa độ của điểm biểu diễn cho số phức là
A. .	B. .	C. .	D. .
Chọn C Ta có: nên .
Do đó, số phức có điểm biểu diễn là .
Câu 7: Cho hai số phức và . Điểm biểu diễn số phức trong mặt phẳng có tọa độ là
A. .	B. .	C. .	D. .
Chọn A Ta có .
Câu 8: Cho bốn điểm , , , trên hình vẽ biểu diễn 4 số phức khác nhau. Chọn mệnh đề sai.
A. là biểu diễn số phức .	B. là biểu diễn số phức .
C. là biểu diễn số phức .	D. là biểu diễn số phức .
Chọn B Theo hình vẽ thì điểm là biểu diễn số phức . Suy ra B sai
Câu 9: Tìm tọa độ điểm biểu diễn của số phức .
A. .	B. .	C. .	D. 
Chọn A Ta có .
Do đó điểm biểu diễn cho số phức có tọa độ .
Câu 10: Cho số phức thoả mãn . Hỏi điểm biểu diễn của là điểm nào trong các điểm , , , ở hình dưới đây? 
A. Điểm .	B. Điểm .	C. Điểm .	D. Điểm .
Chọn C Ta có . Do đó điểm biểu diễn số phức là điểm . 
Câu 11: Điểm biểu diễn của các số phức với nằm trên đường thẳng có phương trình là:
A. .	B. .	C. .	D. .
Chọn B Điểm biểu diễn của các số phức với là .
Rõ ràng điểm thuộc đường thẳng .
Mức độ 3
DẠNG 5:TÌM TẬP HỢP CÁC SỐ PHỨC THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC
MỨC ĐỘ 2:
 Câu 18. (STRONG TEAM TOÁN VD-VDC-ĐỀ MINH HỌA THI THPT QUỐC GIA 2018-2019Cau18) Tìm hai số thực và thỏa mãn với là đơn vị ảo.
A. , .	B. , .	C. , .	D. , .
Lời giải
Chọn D
Ta có: 
Vậy , là hai số cần tìm.
Câu 1. Cho số phức thỏa mãn điều kiện . Số phức liên hợp của là
	A. .	B. .	C. .	D. .
Chọn A
Câu 2. Tìm số phức thỏa mãn .
	A. .	B. .	C. .	D. .
Chọn A Ta có .
Câu 3. Tính môđun của số phức thỏa mãn: 
	A. .	B. .	C. .	D. .
Chọn D Gọi , với 
Ta có 
 .
Câu 4. Có bao nhiêu số phức thỏa mãn ?
	A. .	B. 	C. .	D. .
Chọn B Gọi , . 
.
Vậy có một số phức thỏa mãn yêu cầu bài toán
Câu 5. Cho số phức thỏa mãn điều kiện . Tính .
	A. .	B. .	C. .	D. .
Chọn A Ta có 
Vậy .
Câu 6. Cho số phức thỏa mãn . Tính 
	A. .	B. .	C. .	D. .
Chọn D 
. Vậy 
Câu 7. Cho 2018 phức (trong đó , là các số thực thỏa mãn . Tính .
	A. .	B. .	C. .	D. .
Chọn A Ta có .
Khi đó 
. Vậy .
Câu 8. Cho số phức và thỏa mãn điều kiện . Tính tổng 
	A. .	B. .	C. .	D. .
Chọn A Ta có 
 . Khi đó .
Câu 9. Tìm các số thực , thỏa mãn 
	A. ,.	B. , .	C. , .	D. , .
Chọn C Ta có .
Câu 10. Trên tập số phức cho với . Tính giá trị của biểu thức .
	A. .	B. .	C. .	D. .
Chọn A Ta có .
Vậy .
Câu 11: Tìm các số thực thỏa mãn .
A. .	B. .	C. .	D. .
Chọn D 
Câu 12: Cho hai số thực , thỏa mãn . Khi đó giá trị của bằng
A. .	B. .	C. .	D. .
Chọn A Ta có: 
.
Câu 13: Cho số phức thỏa mãn . Giá trị của bằng
A. .	B. .	C. .	D. .
Chọn A Ta có .
Mà nên .
Câu 14: Có bao nhiêu số phức thỏa mãn ?
A. .	B. .	C. .	D. .
Chọn A Đặt thì 
.
Câu 15: Trong mặt phẳng tọa độ, Gọi , , lần lượt là các điểm biểu diễn số phức , , . Số phức biểu diễn trọng tâm tam giác là
A. .	B. .	C. .	D. .
Chọn B Ta có , , nên trọng tâm của tam giác ABC có tọa độ là . Do đó, số phức biểu diễn điểm là .
MỰC ĐỘ 3:
 Câu 37. (STRONG TEAM TOÁN VD-VDC-ĐỀ MINH HỌA THI THPT QUỐC GIA 2018-2019Cau37) Xét các số phức thỏa mãn là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn số phức là một đường tròn, tâm của đường tròn đó có tọa độ là
A. .	B. .	C. .	D. .
Lời giải
Chọn D
Gọi số phức , .
Ta có:
 là số thuần ảo .
Suy ra tập hợp các điểm biểu diễn số phức là đường tròn có phương trình:
. Tâm của đường tròn là .
Câu 42. (STRONG TEAM TOÁN VD-VDC-ĐỀ MINH HỌA THI THPT QUỐC GIA 2018-2019Cau42) Có bao nhiêu số phức thỏa mãn và ?
A. 4.	B. 3.	C. 1.	D. 2.
Lời giải
Chọn B
Đặt .
	(1)
	(2)
Từ (1) và (2) suy ra 
.
Với , .
Với , .
Với , .
Vậy có tất cả 3 số phức thỏa mãn.
Câu 1: Có bao nhiêu số phức thỏa mãn là số thuần ảo và 
A. .	B. .	C. .	D.Vô số.
Chọn A Đặt với ta có : .
Mà là số thuần ảo nên .Mặt khác 
nên .
Ứng với mỗi ta tìm được một duy nhất, vậy có 2 số phức thỏa mãn yêu cầu bài toán.
Câu 2: Trên mặt phẳng phức tập hợp các số phức thỏa mãn là đường thẳng có phương trình
A. .	B. .	C. .	D. .
Chọn D 
Từ 
Do đó 
.
Câu 3: Biết là số phức thỏa mãn . Tổng là 
A. .	B. .	C. .	D. .
Chọn A Ta có . Theo đề bài ta có 
. Vậy .
Câu 4: Cho số phức , thỏa mãn . Tính .
A. .	B. .	C. .	D. .
Chọn A Ta có : 
. Vậy .
Câu 5: Cho hai số phức và . Biết . Tính . 
A. .	B. .	C. .	D. .
Chọn A Ta có . Vậy .
Câu 6: Tổng phần thực và phần ảo của số phức thoả mãn bằng
A. .	B. .	C. .	D. .
Chọn C Đặt . Khi đó 
, suy ra .
Câu 7: Có bao nhiêu số phức thỏa mãn ?
A. .	B. .	C. .	D. 
Chọn D Gọi , . 
. 
Vậy có một số phức thỏa mãn yêu cầu bài toán.
Câu 8: Có bao nhiêu số phức thỏa mãn ?
A. .	B. .	C. .	D. .
Chọn C Giả sử .
Bài ra ta có Với .
Do đó có 4 số phức thỏa mãn là , , , . 
Câu 9: Cho số phức thỏa mãn và là một số thực. Tính 
A. 	B. 	C. 	D. 
Chọn B 	 
 là số thực nên .
Thay vào ta được 
Câu 10: Cho số phức thỏa mãn và . Tính .
A. .	B. .	C. .	D. .
Chọn D 
Lấy trừ theo vế ta được . Thay vào ta được
. Suy ra .
Do đó có (thỏa điều kiện ). Vậy .
Câu 11: Tập hợp tất cả các điểm biểu diễn các số phức thỏa mãn: là đường tròn có tâm và bán kính lần lượt là:
A. ;.	B. ;.	C. ;.	D. ;.
Chọn A Gọi số phức 
Ta có: 
Vậy tập hợp tất cả các điểm biểu diễn các số phức thỏa mãn: là đường tròn có tâmvà có bán kính .
Câu 12: Cho số phức thoả mãn . Biết rằng tập hợp điểm trong mặt phẳng toạ độ biểu diễn các số phức là một đường tròn. Tìm toạ độ tâm và bán kính của đường tròn đó.
A. , .	B. , .	C. , .	D. , .
Chọn D Đặt . Khi đó .
Vậy tập điểm biểu diễn số phức là đường tròn tâm , bán kính .
Câu 13: Cho là số phức thay đổi thỏa mãn . Trong mặt phẳng phức, các điểm biểu diễn số phức chạy trên đường nào?
A. Đường tròn tâm , bán kính .
B. Đường tròn tâm , bán kính .
C. Đường tròn tâm , bán kính .
D. Đường tròn tâm , bán kính .
Chọn A Gọi là điểm biểu diễn số phức .
Ta có .
Vậy tập hợp điểm cần tìm là đường tròn tâm , bán kính .
Câu 14: Cho số phức thỏa mãn: . Tập hợp các điểm biểu diễn số phức là
A. Đường tròn tâm , bán kính .
B. Đường thẳng có phương trình .
C. Đường thẳng có phương trình .
D. Đường thẳng có phương trình .
Chọn C Gọi ; (, ).
Ta có: .
Vậy tập hợp các điểm biểu diễn số phức là đường thẳng có phương trình .
Câu 15: Đường nào dưới đây là tập hợp các điểm biểu diễn số phức trong mặt phẳng phức thỏa mãn điều kiện ?
A. Một đường thẳng.	B. Một đường tròn.	C. Một đường elip.	D. Một đoạn thẳng.
Chọn A 
Gọi , (với ) được biểu diễn bởi điểm trong mặt phẳng tọa độ .
Ta có 
 (phương trình một đường thẳng).
Câu 16: Tìm tập hợp điểm biểu diễn số phức thoả .
A. Đường tròn tâm , bán kính .	B. Đường tròn tâm , bán kính .
C. Đường tròn tâm , bán kính .	D. Đường tròn tâm , bán kính .
Chọn D Gọi .
Ta có: .
Vậy tập hợp điểm biểu diễn số phức là đường tròn tâm , bán kính .
Câu 17: Xét các số phức thỏa điều kiện . Trong mặt phẳng tọa độ , tập hợp các điểm biểu diễn số phức là?
A. Đường tròn tâm , bán kính .	
B. Đường tròn tâm , bán kính .
C. Đường tròn tâm , bán kính .	
D. Đường tròn tâm , bán kính .
Chọn A Gọi là điểm biểu diễn số phức .
Ta có .
Vậy tập hợp điểm cần tìm là đường tròn tâm , bán kính .
Câu 18: Cho các số phức thỏa mãn . Biết rằng tập hợp điểm biểu diễn số phức là đường tròn. Tính bán kính của đường tròn đó.
A. .	B. .	C. .	D. .
Chọn D Gọi , . Ta có: .
Mà .
Câu 19: Cho số phức thỏa . Biết rằng tập hợp số phức là một đường tròn. Tìm tâm của đường tròn đó.
A. .	B. .	C. .	D. .
Chọn A Đặt 
Ta có .
Mặt khác ta có suy ra hay .
Vây tập hợp số phức là đường tròn tâm .
Câu 20: Cho số phức thỏa mãn và là điểm biểu diễn số phức . Điểm thuộc đường tròn nào sau đây?
A. .	B. .	
C. .	D. .
Chọn B Ta có .
Vậy điểm thuộc đường tròn .
Câu 21: Cho biết có hai số phức thỏa mãn , kí hiệu là và . Tính .
A. .	B. .	C. .	D. .
Chọn D Giả sử: , .
Ta có: .
Ta có . Từ , thay vào , ta được:
.
* (vô nghiệm).
* .
Vậy , . Suy ra .
Câu 22: Cho số phức , thỏa mãn và . Tính .
A. .	B. .	C. .	D. .
Chọn D 
Ta có (1).
 (2). Từ (1) và (2) ta có . Vậy .
Câu 23: Cho số thỏa mãn các điều kiện và . Tìm số phức .
A. .	B. .	C. .	D. .
Chọn D Đặt , với . Ta có
· 
.
· 
.
Ta có hệ phương trình: .
Như vậy .
Câu 24: Cho số phức thỏa mãn và . Tính giá trị của biểu thức .
A. .	B. .	C. .	D. .
Chọn B Theo giả thiết ta có 
Thay vào ta được 
Vì nên . Do đó .
Câu 25: Trong mặt phẳng tọa độ , cho số phức thỏa mãn . Tập hợp các điểm biểu diễn cho số phức là đường tròn
A. Tâm , .	B. Tâm , .	
C. Tâm , .	D. Tâm , .
Chọn A Ta có .
Giả sử 
, .
Câu 26: Cho số phức thỏa mãn . Gọi và lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của . Khi đó bằng
A. .	B. .	C. .	D. .
Chọn C Đặt . Ta có: .
Tập hợp điểm biểu diễn số phức thỏa đề là đường tròn tâm , bán kính .
Khi đó: .