Kiểm tra chất lượng học kì I môn: Toán - Lớp 12 ban cơ bản

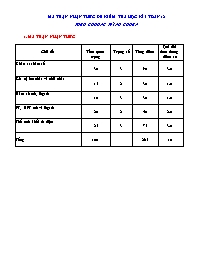
MA TRẬN NHẬN THỨC ĐỀ KIỂM TRA HỌC KÌ I TOÁN 12 
THEO CHƯƠNG TRÌNH CHUẨN
1. MA TRẬN NHẬN THỨC
Chủ đề
Tầm quan trọng
Trọng số
Tổng điểm
Qui đổi theo thang điểm 10
Khảo sát hàm số
30
3
90
3.0
Giá trị lớn nhất và nhỏ nhất
15
2
30
1.0
Hàm số mũ, lôgarit
10
3
30
1.0
PT, BPT mũ và lôgarit
20
2
40
2.0
Thể tích khối đa diện
25
3
75
3.0
Tổng
100
265
10
2. MA TRẬN ĐỀ KIỂM TRA 
Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng điểm
Cấp độ thấp
Cấp độ cao
Khảo sát hàm số
Câu 1a
 2.0
Câu 1b
 1.0
2
 3.0
Giá trị lớn nhất và nhỏ nhất
Câu 3
 1.0
1
 1.0
Hàm số mũ, lôgarit
Câu 5a
 1.0
1
 1.0
PT, BPT mũ và lôgarit
Câu 2
 2.0
2
 2.0
Thể tích khối đa diện
Câu 4a
 1.0
Câu 4b, 5b
 2.0
3
 3.0
Tổng
5 
 6.0
4 
 4.0
9
 10.0
3. MÔ TẢ ĐỀ THI 
Câu
Nội dung
Mức độ
Điểm
1a
Xét tính ĐB, NB của hàm số
Thông hiểu
2.0
Tìm cực trị của hàm số
Thông hiểu
1.0
1b
- Tìm giá trị của tham số để hàm số ĐB, NB trên R
- BL theo m số nghiệm của PT dựa vào đồ thị
Vận dụng
1.0
- Tìm giá trị của tham số để hàm số đạt cực trị tại điểm x = x
- Tìm giá trị của tham số để hàm số có cực trị, không có cực trị
Vận dụng
1.0
2
Giải PT, BPT mũ và lôgarit
Thông hiểu
 2.0
3
Tìm GTLN và GTNN
Thông hiểu
 1.0
4a
Thể tích khối đa diện
Thông hiểu
1.0
5a
Hàm số mũ và lôgarit
Thông hiểu
1.0
4b,5b
Thể tích khối đa diện
Thông hiểu
2.0
KIỂM TRA CHẤT LƯỢNG HỌC KÌ I
Môn: Toán - Lớp 12. Ban cơ bản Năm học: 2011 - 2012
Họ và tên : ..................................... Số báo danh : ............. 
ĐỀ BÀI
Câu 1 ( 3 điểm ): Cho hàm số y = x3 + 3x2 – 2 (1)
	a) Khảo sát và vẽ đồ thị (C) của hàm số.
	b) Tìm m để phương trình 
	 x3 + 3x2 - 1 - m = 0 có 3 nghiệm phân biệt.
Câu 2 ( 2 điểm ) :
	a) Giải phương trình : 
	b) Giải bất phương trình : 
Câu 3 ( 1 điểm ): Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x4 - 2x2 +1
 trên đoạn 
Câu 4 ( 2 điểm ) : Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại đỉnh B, và .Đường thẳng SA vuông góc với mặt phẳng (ABC).
Tính thể tích của khối chóp S.ABC theo a.
Gọi M là trung điểm của SB, N nằm trên cạnh SC sao cho SN = 2NC. Tính thể tích khối chóp S.AMN
Câu 5 (2 điểm) 
Cho hàm số .Chứng minh rằng: .
 b) Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông tâm O, cạnh a, góc SAO bằng 600. Xác định tâm và tính bán kính mặt cầu ngoại tiếp hình chóp .
ĐÁP ÁN
Câu
Nội dung
Điểm
1
+)TXĐ : D=R
0,25
+)BBT: 
x
 -2 0 
 + 0 - 0	+
y
 2 
	(-2)
+)Hàm số đồng biến trên (;-2) và (0; )
+)Hàm số nghịch biến trên (-2;0)
+)Hàm số đạt cực đại tại x=-2 
+) Hàm số đạt cực tiểu tại x=0 
0,25
0,25
0,25
0,25
0,25
*) Vẽ đồ thị: 
+)giao với trục Oy : A(0;-2)
+)giao với trục Ox: là nghiệm của phương trình x3 + 3x2 – 2 =0
+)đồ thị (C): GK tự vẽ
0,25
0,25
Phương trình : x3 + 3x2 – 1- m =0 
Số nghiệm của phương trình đã cho là số giáo điểm của đồ thị (C) và đường thẳng (d): y= m-1.
Để phương trình đã cho có 3 nghiệm thì đường thẳng (d) cắt (C) tại 3 điểm phân biệt tức là : -2< m-1 <2 
Vậy với m thì phương trình đã cho có 3 nghiệm phân biệt
0,25
0,25
0,25
0,25
2
Đặt = t ( Đk: x>0)
Với 
Với 
Vậy phương trình có hai nghiệm x=8 và 
0,25
0,25
0,25
0,25
(1)
Đặt =t (Đk: t >0)
Vậy BPT có tập nghiệm là : T= (0; )
0,25
0,25
0,25
0,25
3
+) TXĐ: D=R
Ta có: y(1)=0; y(3)=64; y(1/2)= 9/16
0,25
0,5
0,25
0,25
4
a)Tính thể tích khối chóp S.ABC.
Ta có: 
----------------------------------------------------------------
b) Ta có 
0,25
0,25
0,25
0,25
1,0
5
a) Chứng minh rằng........: 
Ta có: 
0,25
0,25
0,25
0,25
b) Ta có 
.
Gọi M là trung điểm SA, mặt phẳng trung trực của SA cắt SO tại I suy ra I là tâm mặt cầu cần tìm.
Bán kính R = IS.
Ta có 
R = .
0,25
0,25
0,25
0,25
( Nếu hs làm cách khác đúng vẫn cho điểm tối đa)
--------------------------------------Hết----------------------------