Hướng dẫn ôn tập Toán 12 kì 1

HƯỚNG DẪN ÔN TẬP HỌC KÌ I NĂM HỌC 2008-2009
LỚP 12
GIẢI TÍCH-ĐẠI SỐ
CHƯƠNG I:
☻☻☻1/ Ứng dụng đạo hàm khảo sát và vẽ đồ thị hàm số:
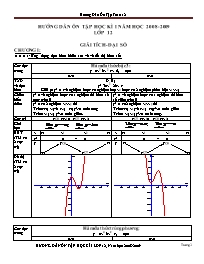
Các đặc trưng
Hàm đa thức bậc 3:
y= ax3+bx2+cx+d, a≠0
a>0
a<0
TXĐ 
và đạo hàm
D=R; 
y’=3ax2+2bx+c
Giải pt y’=0 (vô nghiệm hoặc có nghiệm kép x0 hoặc có 2 nghiệm phân biệt x1<x2)
Chiều biến thiên
y’=0 vô nghiệm hoặc có 1 nghiệm thì hàm số tăng trên R
y’=0 vô nghiệm hoặc có 1 nghiệm thì hàm số giảm trên R
y’=0 có 2 nghiệm x1<x2 thì
Trên (-∞; x1)và (x2; +∞) y’>0 Þhs tăng
Trên ( x1; x2) y’<0 Þ hs giảm.
y’=0 có 2 nghiệm x1<x2 thì
Trên (-∞; x1)và (x2; +∞)y’<0 Þhs giảm
Trên ( x1; x2) y’>0 Þ hs tăng.
Cực trị
yCĐ=y(x1); yCT=y(x2)
yCT=y(x1); yCĐ=y(x2)
Giới hạn
BBT (TH có 2 cực trị)
x
–∞ x1
x2
+∞
x
–∞ x1
x2
+∞
y’
+ 0
– 0
+
y’
+ 0
– 0
+
y
yCĐ
–∞
yCT
+∞
y
+∞
yCT
yCĐ
–∞
Đồ thị
(TH có 2 cực trị)
Các đặc trưng
Hàm đa thức trùng phương:
y= ax4+bx2+c, a≠0
a>0
a<0
TXĐ 
và đạo hàm
D=R;
y’=4ax3+2bx
Giải pt y’=0 (có nghiệm duy nhất bằng 0 hoặc có 2 nghiệm phân biệt -x0<0<x0)
Chiều biến thiên
y’=0 có nghiệm duy nhất x=0 thì
trên(-∞;0) y’<0Þhs giảm
trên(0;+∞)y’>0 Þhs tăng.
y’=0 có nghiệm duy nhất x=0 thì
trên(-∞;0) y’>0Þhs tăng
trên(0;+∞)y’<0 Þhs giảm.
y’=0 có 3 nghiệm -x0<0<x0 thì
Trên (-∞; -x0)và (0; x0) y’<0 Þhs giảm
Trên (-x0; 0)và (x0; +∞) y’>0 Þ hs tăng.
y’=0 có 3 nghiệm -x0<0<x0 thì
Trên (-∞; -x0)và (0; x0) y’>0 Þhs tăng
Trên (-x0; 0)và (x0; +∞) y’<0 Þ hs giảm.
Cực trị
yCT=y(±x0); yCĐ=y(0)=c
yCĐ=y(±x0); yCT=y(0)=c
Giới hạn
BBT
(TH có 3 cực trị)
x
–∞ –x0
0
x0
+∞
x
–∞ –x0
0
x0
+∞
y’
– 0
+ 0
– 0
+
y’
– 0
+ 0
– 0
+
y
+∞
yCT
yCĐ
yCT
+∞
y
yCĐ
–∞
yCT
yCĐ
–∞
Đồ thị
(TH có 3 cực trị)
Các đặc trưng
Hàm hữu tỉ:
 ; ab’-a’b≠0
ab’-a’b>0
ab’-a’b<0
TXĐ 
và đạo hàm
Chiều biến thiên
y’>0 "x Þ Hs tăng trên TXĐ.
y’<0 "x Þ Hs giảm trên TXĐ.
Giới hạn
Tiệm cận
ÞTCĐ ; TCN 	
ÞTCĐ ; TCN 	
Bảng biến thiên
x
–∞ +∞
x
–∞ +∞
y’
+
+
y’
–
–
y
+∞
–∞
y
–∞
+∞
Đồ thị
☻☻2/ Các bài toán liên quan:
a/ Viết phương trình tiếp tuyến của đường cong y=f(x) tại điểm có hoành độ x0:
	Phương trình tiếp tuyến: y=f’(x0)(x-x0)+ f(x0)
b/ Dựa vào đồ thị (C): y=f(x) biện luận số nghiệm của phương trình theo tham số m
	Biến đổi phương trình bề dạng f(x)=g(m); 
	Suy ra số nghiệm của phương trình là số điểm chung của 2 đường: (C) và đường y=g(m) ( là đường thẳng song song với trục hoành.
	Biện luận số giao điểm của hai đường theo vị trí của đường thẳng y=g(m).
c/ Biện luận theo m số cực trị của một hàm số.
	Số cực trị của một hàm số y=f(x) phụ thuộc vào số nghiệm của phương trình y’=0:
	+Hàm bậc 3 chỉ có cực trị (một cực đại và một cực tiểu) khi phương trình y’=0 có 2 nghiệm phân biệt. 
	+Hàm trùng phương có số cực trị bằng số nghiệm của phương trình y’=0 (1 hoặc 3 cực trị).
	+Hàm hữu tỉ không có cực trị.
d/ Tìm giá trị lớn nhất của hàm số trên một đoạn, khoảng.
	Các bước tìm GTLN, GTNN của hàm số y=f(x) trên đoạn [a; b]:
	+Tìm y’=f’(x),
	+Tìm các điểm tới hạn xi ( các điểm mà tại đó y’ không tồn tại hoặc bằng 0),
	+Tính các giá trị f(a), f(b), và f(xi),
	+So sánh các giá trị đó, tìm ra số lớn nhất, số nhỏ nhất.
II. CHƯƠNG II:
☻1. Khảo sát sự biến thiên và vẽ đồ thị hàm số lũy thừa, hàm số mũ và hàm số lôgarit:
	*Tự đọc lại các trường hợp khảo sát và vẽ đồ thị trong SGK.
	Hàm số mũ luôn nằm trên trục hoành và đi qua điểm (0;1).
	Hàm số logarit luôn nằm bên phải trục tung và đi qua điểm (1;0)
	*Lưu ý:Điều kiện của cơ số của lũy thừa và cơ số của lôgarit là số dương và khác 1.
	Điều kiện của biểu thức dưới dấu lôgarit là số dương.
	Mũ của một lũy thừa không có điều kiện.
	*Nắm vững tính đơn điệu của hàm số mũ y=ax, hàm số lôgarit y=logax.
a>0
Hàm số mũ y=ax
Hàm số lôgarit y=logax.
0<a<1
Hàm số giảm
Hàm số giảm
1<a
Hàm số tăng
Hàm số tăng
☻☻2. Giải phương trình, bất phương trình mũ và lôgarit:
 a/ các phương pháp giải phương trình, bất phương trình mũ và lôgarit:
	Đưa về cùng cơ số.
	Đặt ẩn số phụ.
	Lôgarit hóa (phương trình mũ).
	Mũ hóa (phương trình lôgarit).
 b/ Các điểm cần lưu ý khi giải một phương trình, bất phương trình bất kì: 
	Khi chuyển vế một biểu thức, phải đổi dấu biểu thức đó.
	Khi nhân hoặc chia hai vế của một bất đẳng thức với cùng một số âm, phải đổi chiều dấu bất đẳng thức.
	Không được rút gọn nhân tử chung ở hai vế của một phương trình.
	Không được rút gọn nhân tử chung ở hai vế hoặc khử mẫu có chứa ẩn của một bất phương trình.
	Khi tìm được nghiệm của các phương trình, bất phương trình hệ quả, phải kiểm tra lại điều kiện ban đầu.
 c/ Các điểm cần lưu ý khi giải phương trình, bất phương trình mũ và lôgarit:
	Điều kiện của biểu thức dưới dấu logarit.
	Điều kiện của ẩn số phụ. Nếu đặt t=au thì điều kiện là t>0, vì a>0 nên au>0.
	Cần quan sát và nhận xét mối quan hệ của các cơ số, các biểu thức mũ, các biểu thức dưới dấu lôgarit trước khi bắt đầu giải.
 d/ Các công thức thường dùng trong giải phương trình, bất phương trình:
 (an)u=(au)n	dùng để đưa các lũy thừa về cùng cơ số.
 au+m=am.au	làm cho các biểu thức mũ giống nhau, dùng trong phương pháp đặt ẩn phụ
 	đưa các lôgarit về cùng cơ số.
 logaua=alogau	làm cho các biểu thức dưới dấu lôgarit giống nhau®đặt ẩn phụ.
 loga(u.v)=logau+logav	làm giảm số biểu thức lôgarit, hoặc tách một biểu thức lôgarit thành các 	biểu thức lôgarit, tùy theo nhu cầu của bài giải
 logax=bÛx=ab	b=axÛx=logab
 *Tính đơn điệu của hàm số mũ và lôgarit.
HÌNH HỌC
☻1/ Các khái niệm: 
	+Tứ diện, hình chóp, lăng trụ, hình hộp; 
	+Mặt nón, hình nón, mặt trụ, hình trụ, mặt cầu.
	+Đường cao của hình chóp, hình nón, hình trụ; đường sinh của mặt tròn xoay, bán kính của mặt cầu.
	+Các hình đặc biệt: tứ diện đều, hình chóp đều, lăng trụ đứng, hình hộp chữ nhật, hình lập phương, bát diện đều.
	+Mặt cầu ngoại tiếp đa diện là mặt cầu đi qua tất cả các đỉnh của đa diện đó.(lưu ý không phải đa diện nào cũng có mặt cầu ngoại tiếp)
	+Tiếp diện và tiếp tuyến của mặt cầu. 
	 Điều kiện tiếp xúc là khoảng cách từ tâm mặt cầu đến mặt phẳng(đường thẳng) bằng bán kính.
	 Tiếp diện(tiếp tuyến) vuông góc với bán kính tại tiếp điểm.(Nếu O là tâm mặt cầu, H là tiếp điểm thì OH vuông góc với tiếp diện(tiếp tuyến).)
☻2/ Các kết quả:
	+Thiết diện(nếu có) của hình nón cắt bởi mặt phẳng đi qua đỉnh là một tam giác cân.
	+Thiết diện(nếu có) của hình nón cắt bởi mặt phẳng vuông góc với trục là một đường tròn.
	+ Thiết diện(nếu có) của hình trụ cắt bởi mặt phẳng song song với trục là một hình chữ nhật.
	+Giao tuyến(nếu có) của mặt cầu S(O;R) và mặt phẳng(P) là một đường tròn tâm H, bán kính r.
	 Trong đó H là hình chiếu của O lên (P); 
☻☻3/ Các công thức tính diện tích và thể tích: 
Các hình, khối đa diện
Công thức tính thể tích
Chú thích
Hình chóp
B_Diện tích đáy
h_chiều cao
Lăng trụ
Bh
Các hình, khối tròn xoay
Diện tích xung quanh
Thể tích
Chú thích
Nón
Sxq=pRl
B_Diện tích đáy
h_chiều cao; 
l_đường sinh
(trong hình trụ thì h=l)
R_bán kính đường tròn đáy
Trụ
Sxq=2pRl
Bh
Cầu
S=4pR2
R_bán kính
☻4/ Cách xác định tâm mặt cầu ngoại tiếp một hình chóp đều, tứ diện:
	+Xác định trục d của mặt đáy (là đường thẳng đi qua tâm ngoại tiếp của đáy và vuông góc với mặt phẳng đáy).
	+Trong mặt phẳng chứa một cạnh bên, dựng đường trung trực a của cạnh bên đó.
	+Tâm mặt cầu ngoại tiếp là giao điểm của 2 đường thẳng d và a.
☻5/Các kiến thức liên quan:
	+Định lí Pitago trong tam giác vuông: bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
	+Diện tích tam giác bằng nửa tích cạnh đáy với chiều cao tương ứng.
	+Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông.
	+Các công thức diện tích tam giác khác có thể gặp:
	 Trong đó a,b,c là các cạnh đối của các đỉnh A,B,C; p là nửa chu vi tam giác.
☻☻6/ Các bài tập cần lưu ý:
	+Thể tích của hình lập phương, hình hộp chữ nhật,tứ diện, tứ diện đều, tứ diện vuông, hình chóp tam gíac đều, hình chóp đều và các bài toán liên quan đến các hình trên.
	+Diện tích xung quanh, thể tích của các hình(khối) nón, trụ, cầu và các bài toán liên quan đến thiết diện.
	+Tìm tâm và bán kính của hình cầu ngoại tiếp một hình đa diện.