Giáo án môn Giải tích 12 tiết 82: Chỉnh hợp – hoán vị – tổ hợp
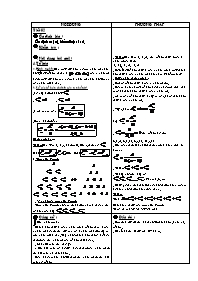
. Thí dụ Cho A = {a, b, c}, các tổ hợp chập 2 của 3 phần tử của A là:
{a, b}, {b, c}, {c, a}
. Hỏi: Một tổ hợp chập k của n phần tử và một chỉnh hợp chập k của n phần tử khác nhau ở điểm nào?
. Hướng dẫn chứng minh :
. Gọi số tổ hợp chập k của n phần tử là s.
. Nếu ta hoàn vị mỗi tổ hợp đó theo đủ mọi cách thì ta có k! chỉnh hợp chập k của n phần tử.
. mà ta có s tổ hợp chập k vậy ta có s.k! số chỉnh hợp chập k của n phần tử
Bạn đang xem tài liệu "Giáo án môn Giải tích 12 tiết 82: Chỉnh hợp – hoán vị – tổ hợp", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
NỘI DUNG
PHƯƠNG PHÁP
Tiết 82
. Ổn định lớp :
Ổn định trật tự, kiểm diện sĩ số.
. Kiểm tra :
. Nội dung bài mới:
4. Tổ hợp
a. Định nghĩa Cho một tập hợp gồm n phần tử phân biệt. Một tổ hợp cha6p k của n phần tử đó là một tập hợp con gồm k phần tử phân biệt trong số n phần tử đã cho.
b. Số các tổ hợp chập k của n phần tử
. Số này được kí hiệu
. .
. 0 < k < n ta có :
. Dạng khai triển:
Chứng minh:
Thí dụ Cho T = {a, b, c, d} tìm C. Các c.thức về
(1) (2)
d. Tam giác Pascal
. Ý nghĩa của tam giác Pascal
Tam giác Pascal giúp ta tính được nhanh chóng các số hãng của dãy
. Thí dụ Cho A = {a, b, c}, các tổ hợp chập 2 của 3 phần tử của A là:
{a, b}, {b, c}, {c, a}
. Hỏi: Một tổ hợp chập k của n phần tử và một chỉnh hợp chập k của n phần tử khác nhau ở điểm nào?
. Hướng dẫn chứng minh :
. Gọi số tổ hợp chập k của n phần tử là s.
. Nếu ta hoàn vị mỗi tổ hợp đó theo đủ mọi cách thì ta có k! chỉnh hợp chập k của n phần tử.
. mà ta có s tổ hợp chập k vậy ta có s.k! số chỉnh hợp chập k của n phần tử.
. Vậy s.k! =
hay
. các tổ hợp đó là :
(a,b,c), (a,b,d), (a,c,d), (b,c,d)
. Các công thức (1) và (2) chứng minh bằng cách áp dụng:
. Thí dụ
. Ta hãy viết các dãy số
với n = 1, 2,
. Nhận xét do tính chất (2) nên biết được hàng trên ta dễ dàng viết được hàng tiếp theo.
Thí dụ
Tính
Nhìn hàng thứ 4 của tam giác Pascal
Ta có : S = 1+ 4 + 6 + 4 + 1 = 16
. Củng cố :
. Cần nhấn mạnh:
Chỉnh hợp chập k của n phần tử và tổ hợp chạp k của n phần tử đều là các tập con có k phần tử được lấy ra từ n phần tử đã cho. Tuy nhiên chỉnh hợp thì có kể đến thứ tự của các phần tử còn tổ hợp thì không.
. Khi giải toán cần chú ý:
- Các bài toán có đề cập đến thứ tự của phần tử là các bài toán và chỉnh hợp.
Nếu không phân biệt thứ tự các phần tử là các bài toán về tổ hợp.
. Dặn dò :
. Học sinh lập lại các khai niệm chỉnh hợp, hoán vị, tổ hợp.
. Chuẩn bị các ài tập mà GV đã ra.
Tài liệu đính kèm:
 GT-T82.doc
GT-T82.doc





