Giáo án môn Giải tích 12 tiết 36: Khảo sát hàm số. Bài tập
Tiết 36 Phần luyện tập:
. Ổn định lớp :
Ổn định trật tự, kiểm diện sĩ số.
. Kiểm tra:
. Nội dung bài mới:
Bài tập 1 Cho (Cm) : y = -x4 + mx2 + 1 – m
1) CMR: (Cm) luôn qua 2 điểm cố định A,B (giả sử xa > 0)
2) Định m để tiếp tuyến tại A song song với đường thẳng (D) : y = -2x
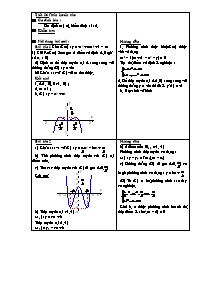
30 Khảo sát vẽ (C) với m tìm được.
Bạn đang xem tài liệu "Giáo án môn Giải tích 12 tiết 36: Khảo sát hàm số. Bài tập", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Tiết 36 Phần luyện tập: . Ổn định lớp : Ổn định trật tự, kiểm diện sĩ số. . Kiểm tra: . Nội dung bài mới: Bài tập 1 Cho (Cm) : y = -x4 + mx2 + 1 – m 1) CMR: (Cm) luôn qua 2 điểm cố định A,B (giả sử xa > 0) 2) Định m để tiếp tuyến tại A song song với đường thẳng (D) : y = -2x 30 Khảo sát vẽ (C) với m tìm được. Kết quả 1. A(1, 0), B(-1, 0) ; 2. m = 1 ; 3. (C) : y – x4 + x2 Hướng dẫn 1. Phương trình thực hiện(Cm) được viết về dạng (x2 – 1)m + (1 – x4 – y) = 0 Tọa độ điểm cố định là nghiệm : 2. Để tiếp tuyến tại A(1,0) song song với đường thẳng y = -2x thì đk là y’(1) = -2 3. Học sinh vẽ hình Bài tập 2 a) Khảo sát và vẽ (C) : y = x4 – 3x2 + b) Viết phương trình tiếp tuyến của (C) tại điểm uốn. c) Tìm các tiếp tuyến của (C) đi qua A(0,) Kết quả b) Tiếp tuyến tại (-1,-1) (D1) : y = 4x + 3 Tiếp tuyến tại (1,-1) (D2) = y2 – 4x + 3 c) Các tiếp tuyến qua A(0,) (D1,2) : y = ± ; (D3) : y = Hướng dẫn b) 2 điểm uốn M1,2 (±1, -1) Phương trình tiếp tuyến có dạng : (D) : y – y0 = f’(x0).(x –x0) c) Đường thẳng (D) đi qua A(0,) có bsg k phương trình có dạng : y = kx + (D) Tx (C) Û hệ phương trình sau đây có nghiệm. Khử k, ta được phương trình hoành độ tiếp điểm là : 3x2.(x – 2) = 0 Bài tập 3 : Cho hàm số y = -x4 + 2mx2 – 2m + 1 có đồ thị (Cm) a) Biện luận theo m số cực trị của (Cm) b) Định m sao cho (Cm) cắt Ox tại 4 điểm có hoành độ lập thành cấp số cộng. c) Khảo sát và vẽ (C5) Kết quả a) m £ 0 : một cực đại (tại x = 0) m > 0 : hai cực đại (tại x = 2) và một cực tiểu tại x = 0 b) . m = 5 -3, -1, 1, 3 . m = -1, -,, 1 Hướng dẫn a) y’ = -4x(x2 – m) . Cho HS xét các trường hợp m £ 0, m> 0. b) Phương trình hoành độ giao điểm (Cm) và Cx. x4 – 2mx2 + 2m – 1 = 0 (1) Điều kiện là phương trình (2) phải có 2 nghiệm t1, t2 > 0 sao cho t2 = 9t1. Suy ra : 9m2 – 50m + 25 = 0 . Củng cố : Bài tập (bổ sung) Cho (Cm) : y = x4 – mx2 + 2m + 5 a) Khảo sát vẽ (C) khi m = -2 b) Tìm các điểm cố định của (Cm) c) Biện luận theo m số giao điểm của (Cm) và Ox Hướng dẫn câu c) Ta cần nghiên cứu số N0 của pt x4 – mx2 + 2m + 5 = 0 (*) Đặt t = x2 pt (*) trở thành :t2 – mt + 2m + 5 = 0 (1) Muốn biến số nghiệm (*) ta cần khảo sát số nghiệm t ³ 0 của (1) Bài toán trở thành biện luận số nghiệm t ³ 0 của (1) . Ta phải tính D, P, S . Dặn dò : - Xem lại các qui tắc tìm tiệm cận. - Đọc trước bài khảo sát hàm số y = D. RÚT KINH NGHIỆM . . . . . . . . . . . . .
Tài liệu đính kèm:
 C2-36.doc
C2-36.doc





