Giáo án lớp 12 môn Hình học - Tiết 11: Đề kiểm tra 1 tiết chương I

Tiết 11
ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG I
I/ MỤC ĐÍCH YÊU CẦU
a/ Kiến thức:
Học sinh biết khái niệm lăng trụ, khối chop, các khối đa diện
HS biết phép đối xứng qua mặt phẳng và sự bằng nhau của hai khối đa diện 
HS biết khái niệm của các khối đa diện đều 
Biết các công thức tính thể tích các khối lăng trụ và chóp
b/ Kỷ năng:
HS giải được dạng bài tập liên quan
Tính được thể tích khối lăng trụ và chop
II/ MỤC TIÊU
Nhận biết được các khối đa diện và khối đa diện đều
Biết cách phân chia và lắp ghép
Nắm vững các công thức vận dụng và tính được thể tích
Nắm vững lý thuyết rèn luyện kỷ năng giải bài tập và giúp cho bài giảng chương sau.
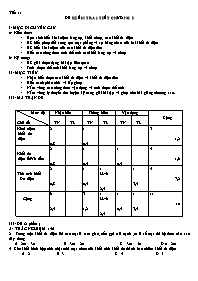
III/ MA TRẬN ĐỀ
 Mức độ
Chủ đề 
 Nhận biết
 Thông hiểu
 Vận dụng
 Cộng 
 TN
 TL
 TN
 TL
 TN
 TL
Khái niệm
 khối đa 
 diện 
2
 0,8
1
 0,4
3
 1,2
Khối đa 
 diện lồiVà đều
2
 0,8
1
 0,4
1
 0,4
4
 1,6
Thể tích khối 
 Đa diện
2
 0,8
1
 0,4
1+ H.vẽ
 2,5
1
 3,5
4
 7,2
 Cộng
6
 2,4
3
 1,2
1+ H.vẽ
 2,5
1
 0,4
1
 3,5
11
 10
III/ ĐỀ (2 phần )
A/ TRẮC NGHIỆM : 4đ
2 Trong một khối đa diện lồi các mặt là tam giác, nếu gọi c là cạnh ,m là số mặt thì hệ thức nào sau đây đúng
 A 2m = 3c B 3m = 2c C 3m = 5c D c = 2m
4 Cho khối hình hộp chữ nhật mỗi mặt chéo của khối chia khối đó thành bao nhiêu khối đa diện 	 A 2 B 3 C 4 D 5
5 Tìm mệnh đề đúng trong các mệnh đề sau :
 I Số cạnh của khối đa diện lồi lớn hơn hoặc bằng sáu
 II Số mặt của khối đa diện luôn lớn hơn hoặc bằng năm 
 III Số đỉnh của khối đa diện lớn hơn bốn
 A Chỉ I B Chỉ II C I và II D I và III 
6 Cho khối lăng trụ tam giac đều ABC.A’B’C’.Về phía ngoài của khối lăng trụ này ta ghép thêm một khối lăng trụ tam giác đều bằng với khối lăng trụ đã cho sao cho hai khối lăng trụ có chung một mặt bên. Hỏi khối đa diện mới lâp thành có mấy cạnh ?
 A 9 B 12 C 15 D 18
7 Cho khối lăng trụ tam giác ABC.A’B’C’có thể tích V .Trên (A’B’C’)lấy M bất kỳ .Thể tích khối chóp M.ABC Tính theo V bằng
 A V/2 B 2V/3 C V/3 D 3V/4
9 Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
 A 1 B 2 C 3 D 4
Câu 2 : (NB) Số mặt phẳng đối xứng của hình tứ diện đều :
	A/ 4	B/ 6	C/8	D/ 10
Câu 4 : (TH ) Trong một khối đa diện lồi với các mặt là tam giác. Nếu gọi C là số
cạnh và M là số mặt thì hệ thức nào sau đây đúng ?
	A/ 2M = 3C	B/ 3M = 2C	C/ 3M = 5C	D/ C = 2M
Câu 5 : (NB) Khối 12 mặt thuộc loại nào:
	A/ { 3;5 }	B/ { 3; 6 }	C/ { 5; 3 }	D/ { 4 ; 4}
Câu 6 : ( VD ) Một hình chóp tam giác đều có cạnh bên bằng b và chiều cao bằng h .Khi đó thể tích hình chóp là :
 A/	B/ 	C/ D/	
Câu 7 : ( VD ) Cho hình lập phương ABCD.A’B’C’D’ cạnh a tâm O khi đó thể tích khối tứ diện AA’B’O là :
	A/ 	B/ 	C/ 	D/ 
Câu 10 : (VD ) Cho hình hộp ABCD.A’B’C’D’. Gọi O là giao điểm của AC & BD
tỉ số thể tích khối chóp O.A’B’C’D’ và khối hộp ABCD.A’B’C’D’ bằng :
	A/ 	B/	C/ 	D/ 
Câu 2(NB): Chọn khẳng định sai. Trong một khối đa diện:
	A/ Hai mặt bất kỳ luôn có ít nhất một điểm chung;	B/ Mỗi đỉnh là đỉnh chung của ít nhất 3 mặt;
	C/ Mỗi mặt có ít nhất ba cạnh;	D/ Mỗi cạnh của một khối đa diện cũng là cạnh chung của đúng 2 mặt;
.
II TỰ LUẬN : 6đ
 Cho hình chóp S.ABC vơi ABC là tam giác đều cạnh a SA vuông góc với (ABC), SA= h .Gọi H,I là trựctâm
 của tam giác ABC và tam giác SBC 
 1 chứng minh IH vuông góc (SBC)
 2 Tính thể tich tứ diện IHBC theo a và h 
 ĐÁP ÁN
 I/ Trắc nghiệm :
 Gồm 10 câu mỗi câu 0,4đ 
Câu 1
Câu2
Câu3
Câu4
Câu5
Câu6
Câu7
Câu8
Câu9
Câu10
C
B
D
A
A
B
C
D
D
A
 II / Tự luận: (6đ)
S
A
B
C
E
F
H
I
+ Vẽ hình đúng (0,5đ)
 1/ (2đ)
Gọi E là trung điểm của BC ta có I € SE, H € AE (0,5 đ) 
- Chứng minh được BC IH (0,5 đ)
- Chứng minh được SC IH (0,5đ)
 Suy ra IH (SBC) (0,5đ)
2) 
 Chứng minh được ASE và IHE đồng dạng (0,5đ)
HE
SE
IE
AE
IH
SA
	Suy ra 
	= = (0,5đ)
IH = 
3
ah 
4h2 + 3a2
(0,5đ)
3
Tính đúng 	 	 
IE = 
4h2 + 3a2
a2
2
(0,5đ)
(0,5đ)
 = 
4h2 + 3a2
a3
4
S
BIC
BIC
(0,5đ)
S
BIC
BIC
HI.
1
3
=
V
 H.IBC
Viết đúng công thức: 
Kết luận đúng (0,5đ)