Giáo án Hình học lớp 12 - Chương 3: Phương pháp toạ độ trong không gian

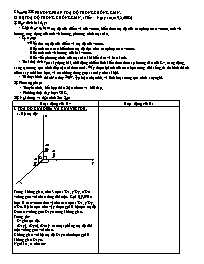
Chương III: PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN.
Œ HỆ TOẠ ĐỘ TRONG KHÔNG GIAN. (Tiết: Ngaøy soaïn: 9.8.2008)
I. Mụcđñích baøi dạy:
 - Kiến thức cơ bản: toạ độ của điểm và của vector, biểu thức toạ độ của các phép toán vector, tích vô hướng, ứng dụng của tích vô hướng, phương trình mặt cầu, 
 - Kỹ năng: 
 + Biết tìm toạ độ của điểm và toạ độ của vector.
 + Biết tính toán các biểu thức toạ độ dựa trên các phép toán vector.
 + Biết tính tích vô hướng của hai vector.
 + Biết viết phương trình của mặt cầu khi biết tâm và bán kính.
 - Thaùi ñoä: tích cực xây dựng bài, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của Gv, năng động, sáng tạo trong quá trình tiếp cận tri thức mới, thấy được lợi ích của toán học trong đời sống, từ đó hình thành niềm say mê khoa học, và có những đóng góp sau này cho xã hội.
 - Tö duy: hình thành tư duy logic, lập luận chặt chẽ, và linh hoạt trong quá trình suy nghĩ.
II. Phương phaùp: 
 - Thuyết trình, kết hợp thảo luận nhoùm vaø hỏi ñaùp.
 - Phöông tieän daïy hoïc: SGK. 
III. Nội dung vaø tiến trình leân lớp:
Hoạt đñộng của Gv
Hoạt đñộng của Hs
I. TOẠ ĐỘ CỦA ĐIỂM VÀ CỦA VECTOR. 
x
y
z
O
 1. Hệ toạ độ:
Trong không gian, cho 3 trục x’Ox, y’Oy, z’Oz vuông góc với nhau từng đôi một. Gọi lần lượt là các vector đơn vị trên các trục x’Ox, y’Oy, z’Oz. Hệ ba trục như vậy được gọi là hệ trục toạ độ Decarst vuông góc Oxyz trong không gian.
Trong đó:
+ O: gốc tọa độ.
+ (Oxy), (Oyz), (Ozx): các mặt phẳng toạ độ đôi một vuông góc với nhau.
Không gian với hệ toạ độ Oxyz còn được gọi là không gian Oxyz.
Ngoài ra, ta còn có:
 Hoạt động 1:
 Trong không gian Oxyz, cho điểm M. Hãy phân tích vector theo ba vector không đồng phẳng đã cho trên các trục Ox, Oy, Oz.
2. Toạ độ của một điểm:
 Trong không gian Oxyz, cho điểm M tuỳ ý. Vì ba vetor không đồng phẳng nên có một bộ ba số (x; y; z) duy nhất sao cho:
 = x. + y. + z. (H.3.2, SGK, trang 63)
 Ngược lại, với bộ ba số (x; y; z) ta có một điểm M duy nhất thoả : = x. + y. + z. 
 Khi đó ta gọi bộ ba số (x; y; z) là toạ độ của điểm M. Ta viết: M(x; y; z) (hoặc M = (x; y; z))
 x: hoaønh ñoä ñieåm M.
 y: tung ñoä ñieåm M.
 z: cao ñoä ñieåm M. 
3. Toạ độ của vector:
 Trong không gian Oxyz cho vector , khi đó luôn tồn tại duy nhất bộ ba số (a1; a2; a3) sao cho: = a1. + a2. + a3. . Ta gọi bộ ba số (a1; a2; a3) là toạ độ của vector . Ta viết : 
 = (a1; a2; a3) hoặc (a1; a2; a3)
* Nhận xét: M (x; y; z) Û 
 Hoạt động 2:
 Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O, có 
; ; theo thứ tự cùng hướng với và có AB = a, AD = b, AA’ = c. Hãy tính toạ độ các vector ; ; và với M là trung điểm của cạnh C’D’.
II. BIỂU THỨC TOẠ ĐỘ CỦA CÁC PHÉP TOÁN VECTOR.
 Gv giới thiệu với Hs nội dung định lý sau:
“Trong không gian Oxyz cho hai vector và . Ta có:
a) .
b) .
c) Vôùi k Î R Þ 
Phần chứng minh, Gv hướng dẫn Hs xem SGK, trang 64.
 * Hệ quả:
 a/ Cho hai vector và . Ta có:
b/ Vector có toạ độ là (0; 0; 0)
c/ Với thì hai vector và cùng phương khi và chỉ khi có một số k sao cho :
d/ Ñoái vôùi heä toïa ñoä Oxyz cho hai ñieåm baát kyø A(xA ; yA ; zA) vaø B(xB ; yB ; zB) thì ta coù coâng thöùc sau : 
 + Toïa ñoä trung ñieåm I cuûa ñoaïn AB là 
III. TÍCH VÔ HƯỚNG. 
 1. Biểu thức toạ độ của tích vô hướng:
 Ñònh lyù : Trong không gian vôùi heä toïa ñoä Oxyz, bieåu thöùc toïa ñoä cuûa tích voâ höôùng hai veùctô , được xác định bởi công thức : 
 2. Ứng dụng:
 a/ Độ dài của một vector: 
 b/ Khoảng cách giữa hai điểm:
 c/ Góc giữa hai vector:
 Neáu goïi j laø goùc hôïp bôûi hai veùctô , vôùi thì 
Vaäy ta coù coâng thöùc tính goùc giöõa hai veùctô , vôùi nhö sau :
 Suy ra: 
 Hoạt động 3:
 Với hệ toạ độ Oxyz trong không gian, cho = (3; 0; 1), = (1; - 1; - 2), = (2; 1; - 1). Hãy tính 
 và .
IV. MẶT CẦU.
 Gv giới thiệu với Hs nội dung định lý sau:
“Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c) bán kính r có phương trình là: ”
 Gv giới thiệu với Hs phần chứng minh (SGK, trang 67) để Hs hiểu rõ và biết cách viết phương trình mặt cầu khi biết toạ độ tâm và bán kính r.
 Hoạt động 4:
 Em hãy viết phương trình mặt cầu tâm I(1; - 2; 3) và có bán kính r = 5.
* Nhận xét:
Mặt cầu trên có thể viết dưới daïng :
x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0 vôùi 
d = a2 + b2 + c2 – r2.
 Người ta đã chứng minh được rằng phương trình 
x2 + y2 + z2 + 2Ax + 2By + 2Cz + D = 0 vôùi 
A2 + B2 + C2 – D > 0 là phương trình mặt cầu tâm I(- A; - B; - C), bán kính . 
 Gv giới thiệu với Hs vd (SGK, trang 67, 68) để Hs hiểu rõ và biết cách viết phương trình mặt cầu ở dạng triển khai.
Hs thảo luận nhóm để phân tích vector theo ba vector không đồng phẳng đã cho trên các trục Ox, Oy, Oz.
Hs thảo luận nhóm để tính toạ độ các vector ; ; và với M là trung điểm của cạnh C’D’.
Hs thảo luận nhóm để tính và .
Hs thảo luận nhóm để viết phương trình mặt cầu tâm I(1; - 2; 3) và có bán kính r = 5.
IV. Củng cố:
	+ Gv nhắc lại các khái niệm và quy tắc trong bài để Hs khắc sâu kiến thức.
	+ Dặn BTVN: 1..6, SGK, trang 68.
 PHƯƠNG TRÌNH CỦA MẶT PHẲNG. (Tiết: Ngaøy soaïn: 10.8.2008)
I. Mụcđñích baøi dạy:
 - Kiến thức cơ bản: vector pháp tuyến của mặt phẳng, phương trình tổng quát của mặt phẳng, điều kiện để hai mặt phẳng song song, vuông góc, khoảng cách từ một điểm đến một mặt phẳng.
 - Kỹ năng: 
 + Biết tìm toạ độ của vector pháp tuyến của mặt phẳng.
 + Biết viết phương trình tổng quát của mặt phẳng.
 + Biết chứng minh hai mặt phẳng song song, hai mặt phẳng vuông góc.
 + Biết tính khoảng cách từ một điểm đến một mặt phẳng.
 - Thaùi ñoä: tích cực xây dựng bài, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của Gv, năng động, sáng tạo trong quá trình tiếp cận tri thức mới, thấy được lợi ích của toán học trong đời sống, từ đó hình thành niềm say mê khoa học, và có những đóng góp sau này cho xã hội.
 - Tö duy: hình thành tư duy logic, lập lu
 PHƠNG TRÌNH CỦA MẶT PHẲNG. (Tiết: Ngaøy soaïn: 10.8.2008)
I. Mụcđñích baøi dạy:
 - Kiến thức cơ bản: vector pháp tuyến của mặt phẳng, phương trình tổng quát của mặt phẳng, điều kiện để hai mặt phẳng song song, vuông góc, khoảng cách từ một điểm đến một mặt phẳng.
 - Kỹ năng: 
 + Biết tìm toạ độ của vector pháp tuyến của mặt phẳng.
 + Biết viết phương trình tổng quát của mặt phẳng.
 + Biết chứng minh hai mặt phẳng song song, hai mặt phẳng vuông góc.
 + Biết tính khoảng cách từ một điểm đến một mặt phẳng.
 - Thaùi ñoä: tích cực xây dựng bài, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của Gv, năng động, sáng tạo trong quá trình tiếp cận tri thức mới, thấy được lợi ích của toán học trong đời sống, từ đó hình thành niềm say mê khoa học, và có những đóng góp sau này cho xã hội.
 - Tö duy: hình thành tư duy logic, lập luận chặt chẽ, và linh hoạt trong quá trình suy nghĩ.
II. Phương phaùp: 
 - Thuyết trình, kết hợp thảo luận nhoùm vaø hỏi ñaùp.
 - Phöông tieän daïy hoïc: SGK. 
III. Nội dung vaø tiến trình leân lớp:
Hoạt đñộng của Gv
Hoạt đñộng của Hs
I. VECTOR PHÁP TUYẾN CỦA MẶT PHẲNG.
 Định nghĩa:
 Cho mặt phẳng (a). Nếu vector khác và có giá vuông góc với mặt phẳng (a) thì được gọi là vector pháp tuyến của (a).
 * Chú ý: Nếu vector là vector pháp tuyến của mặt phẳng (a) thì vector k cũng là vector pháp tuyến của (a).
 Gv giới thiệu với Hs bài toán (SGK, trang 70) để Hs hiểu rõ và biết cách tìm vector pháp tuyến của mặt phẳng bằng cách tính tích có hướng của hai vector có giá song song hoặc nằm trong mp (a).
 Hoạt động 1:
 Trong không gian Oxyz, cho ba điểm A(2; - 1; 3), B(4; 0; 1), C(- 10; 5; 3). Hãy tìm vector pháp tuyến của mp (ABC)?
II. PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG.
 Qua việc giới thiệu hai bài toán 1, 2 (SGK, trang 71, 72) cho Hs , Gv làm nổi bật lên hai vấn đề sau cho Hs nắm được:
+ Vấn đề 1: Điều kiện cần và đủ để điểm M(x; y; z) thuộc mp (a) là 
A(x – x0) + B(y – y0) + C(z – z0) = 0
+ Phương trình Ax + By + Cz + D = 0 là một mặt phẳng nhận vector = (A; B; C) làm vector pháp tuyến của mp.
 Từ đó, đi đến định nghĩa sau:
1. Định nghĩa:
“Phương trình có dạng Ax + By + Cz + D = 0, (1) trong đó A, B, C không đồng thời bằng 0, được gọi là phương trình tổng quát của mặt phẳng.” 
* Nhận xét:
a) Neáu (a) coù pt : Ax + By + Cz + D = 0 thì laø moät veùctô phaùp tuyeán cuûa noù .
b) Neáu mp(a) ñi qua ñieåm M0(x0 ; y0 ;z0) vaø coù veùctô phaùp tuyeán thì phöông trình cuûa noù coù daïng :
 Hoạt động 2:
 Em hãy tìm một vector pháp tuyến của mặt phẳng (a): 4x – 2y – 6z + 7 = 0.
 Hoạt động 3:
 Em hãy lập phương trình tổng quát của mặt phẳng (MNP) với M(1; 1; 1), N(4; 3; 2), P(5; 2; 1).
2. Các trường hợp riêng:
 a) Neáu D = 0 thì mp(1) ñi qua goác taïo ñoä (H3.6, SGK, trang 72)
b) Neáu thì mp(1) chöùa hoaëc song song vôùi truïc Ox. (H3.7, SGK, trang 72)
 Hoạt động 4:
 Nếu B = 0 hoặc C = 0 thì mặt phẳng (1) có đặc điểm gì? 
c) Neáu ptrình mp coù daïng : Cz + D = 0 thì maët phaúng ñoù song song hoaëc truøng vôùi mp (Oxy). (H3.8, SGK, trang 72)
 Hoạt động 5:
 Nếu A = C = 0 và B ≠ 0 hoặc B = C = 0 và A ≠ 0 thì mặt phẳng (1) có đặc điểm gì? 
* Nhận xét:
 Neáu A , B , C , D ¹ 0 thì baèng caùch ñaët nhö sau : ta coù phöông trình daïng : vaø ñöôïc goïi laø phöông trình cuûa maët phaúng theo ñoaïn chaén (Hay noùi caùch khaùc phöông trình treân laø phöông maët phaúng ñi qua 3 ñieåm naèm treân 3 truïc Ox , Oy , Oz laàn löôït laø : (a ; 0 ; 0) , (0 ; b ; 0) , (0 ; 0 ;c)) .
 Gv giới thiệu với Hs vd (SGK, trang 74) để Hs hiểu rõ và biết cách viết phöông trình cuûa maët phaúng theo ñoaïn chaén.
III. ĐIỀU KIỆN ĐỂ HAI MẶT PHẲNG SONG SONG, VUÔNG GÓC.
 Hoạt động 6:
 Cho hai mặt phẳng (a) và (b) có phương trình:
(a): x – 2y + 3z + 1 = 0
(b): 2x – 4y + 6z + 1 = 0
Em có nhận xét về toạ độ hai vector pháp tuyến của hai mặt phẳng này ?
1. Điều kiện để hai mặt phẳng song song :
 Ta thấy hai mặt phẳng song song với nhau khi và chỉ khi hai vector pháp tuyến của chúng cùng phương. (H.3.10)
 Khi đó ta có : 
 Nếu D1 = kD2 thì ta có hai mặt phẳng trùng nhau.
 Nếu D1 ≠ kD2 thì hai mặt phẳng song song với nhau.
 Từ đó ta có :
* Chú ý:
 Hai mặt phẳng cắt nhau 
 Gv giới thiệu với Hs vd (SGK, trang 76) để Hs hiểu rõ và biết cách viết phöông trình cuûa maët phaúng khi biết nó song song với mặt phẳng khác.
2. Điều kiện để hai mặt phẳng vuông góc: 
 Ta thấy hai mặt phẳng vuông góc với nhau khi và chỉ khi hai vector pháp tuyến của chúng vuông góc với nhau.
 Do đó ta có:
 Gv giới thiệu với Hs vd (SGK, trang 76) để Hs hiểu rõ và biết cách viết phöông trình cuûa maët phaúng khi biết nó vuông góc với mặt phẳng khác.
IV. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG.
 Gv giới thiệu với Hs nội dung định lý sau:
“Trong khoâng gian vôùi heä toïa ñoä Oxyz cho maët phaúng (a) coù phöông trình : Ax + By + Cz + D = 0 vaø ñieåm M0(x0 ; y0 ; z0). Khoaûng caùch töø ñeåm M0 ñeán mp(a) ký hiệu là d(M0 , (a)), được tính bởi công thức :
 Gv hướng dẫn Hs đọc phần chứng minh của SGK, trang 78, để hiểu rõ định lý vừa nêu.
 Gv giới thiệu với Hs vd 1, 2 (SGK, trang 79) để Hs hiểu rõ và biết cách tính khoaûng caùch töø ñeåm M0 ñeán mp(a).
 Hoạt động 7:
 Em hãy tính khoảng cách giữa hai mặt phẳng sau:
(a): x – 2 = 0
(b):x – 8 = 0
Hs thảo luận nhóm để tìm vector pháp tuyến của mp (ABC).
+ Tính 
+ Tính 
+ Tính (hay 
Hs thảo luận nhóm để
+ Tìm một vector pháp tuyến của mặt phẳng (a): 4x – 2y – 6z + 7 = 0.
+ Lập phương trình tổng quát của mặt phẳng (MNP) với M(1; 1; 1), N(4; 3; 2), P(5; 2; 1).
 . Tính 
 . Tính 
 . Tính (hay 
 . Lập phương trình mặt phẳng.
Hs thảo luận nhóm để tìm xem khi B = 0 hoặc C = 0 thì mặt phẳng (1) có đặc điểm gì. (Dựa vào trường hợp A = 0)
Hs thảo luận nhóm để tìm toạ độ hai vector pháp tuyến của hai mặt phẳng này và nhận xét.
Hs thảo luận nhóm để tính khoảng cách giữa hai mặt phẳng sau:
(a): x – 2 = 0
(b): x – 8 = 0
IV. Củng cố:
	+ Gv nhắc lại các khái niệm và quy tắc trong bài để Hs khắc sâu kiến thức.
	+ Dặn BTVN: 1..10, SGK, trang 80, 81.