Giáo án Hình học 12: Khối đa diện lồi – khối đa diện đều

§ 2 : KHỐI ĐA DIỆN LỒI – KHỐI ĐA DIỆN ĐỀU
Mục đích – Yêu cầu : HS hiểu thế nào là khối đa diện lồi , khối đa diện đều , Nhận biết các khối đa diện đều.
Trọng tâm : Các định nghĩa .
Các bước lên lớp :
Ổn định lớp.
Kiểm tra bài cũ : Vẽ một khối lập phương và chia khối đó thành 4 khối tứ diện
Bài học:
Hoạt động của thầy và trò
Nội dung bài học
GV phát biểu định nghĩa và giải thích.
HS cho thêm ví dụ về khối đa diện lồi và khối đa diện không lồi.
GV nhận định và kết luận
Cho HS chứng minh các mặt của bát diện là các tam giác đều.
·
·
·
·
·
·
·
·
·
·
·
·
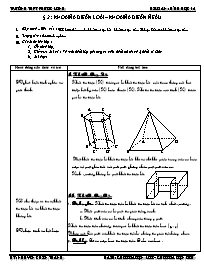
I. Khối Đa Diện Lồi 
Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kỳ của (H) luôn thuộc (H). Khi đó đa diện xác định (H) được gọi là đa diện lồi.
 A F S 
 B E
 C D 
 A’ F’ A D 
 B’ E’
 C’ D’ B C 
 Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng chứa một mặt của nó.
Hình sau đây không là một khối đa diện lồi.
II. Khối Đa Diện Đều
1. Định nghĩa : Khối đa diện đều là khối đa diện lồi có tính chất sau đây :
	a. Mỗi mặt của nó là một đa giác đều p cạnh.
	b. Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p ; q}
Nhận xét: Các mặt của khối đa diện đều là những đa giác đều bằng nhau.
2. Định lý : Chỉ có năm loại đa diện đều. Đó là các loại : 
	{3;3} : Tứ diện đều 
	{4;3} : Lập phương
	{3;4} : Bát diện đều
	{5;3} : Mười hai mặt đều
	{3;5} : Hai mươi mặt đều.
Bảng tóm tắt của năm loại khối đa diện đều : 
Loại
Tên gọi
Số đỉnh
Số cạnh
Số mặt
{3 ; 3}
{4 ; 3}
{3 ; 4}
{5 ; 3}
{3 ; 5}
Tứ diện đều 
Lập phương
Bát diện đều
Mười hai mặt đều
Hai mươi mặt đều
4
8
6
20
12
6
12
12
30
30
4
6
8
12
20
3. Ví dụ : Chứng minh rằng
a. Trung điểm các cạnh của một tứ diện đều là các đỉnh của một bát diện đều.
b. Tâm các mặt của một hình lập phương là các đỉnh của một bát diện đều.
Giải :
a. Cho tứ diện đều ABCD cạnh a. Gọi M, N , P , Q , R , S lần lượt là trung điểm các cạnh AC , BD , AB , BC , CD , DA.
Nối các trung điểm ta được một hình bát diện MNPQRS, trong đó các mặt của của nó là các tam giác đều và mỗi đĩnh của nó là đỉnh chung của đúng 4 tam giác đều vậy đa diện ấy chính là bát diện đều.
b. Sáu tâm cũng chính là 6 trung điểm của tứ diện đều AB’CD’ nên theo câu a đa diện ấy chính là bát diện đều.
Dạng bài tập chứng minh tính chất một hình đa diện : Chứng minh 
PQRS là một hình vuông.
Củng cố : 
	1 . Nhắc lại các khái niệm. 
	2. Phân chia một khối chóp S.ABCD thành ba khối có đỉnh là các đỉnh của khối chóp ban đầu không ?
Dặn dò : Về nhà học bài và làm đầy đủ bài tập trong SGK.