Giáo án Hình học 12: Khái niệm về khối đa diện

Chương I
KHỐI ĐA DIỆN
§ 1 : KHÁI NIỆM VỀ KHỐI ĐA DIỆN
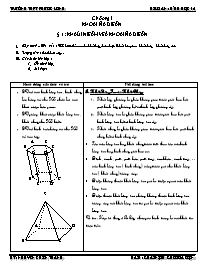
Mục đích – Yêu cầu : HS hiểu thế nào là khối hộp chữ nhật. Khối lăng trụ, khối chóp , khối chóp cụt.
Trọng tâm : Các khái niệm.
Các bước lên lớp :
Ổn định lớp.
Bài học:
Hoạt động của thầy và trò
Nội dung bài học
GV vẽ các hình lăng trụ , hình chóp lên bảng và cho HS nhắc lại các khái niệm liên quan.
GV giảng khái niệm khối lăng trụ , khối chóp cho HS hiểu. 
GV vẽ hình trên bảng và cho HS vẽ vào tập.
 A F 
 B E
 C D 
 A’ F’
 B’ E’
 C’ D’ 
 S 
 A D 
 B C 
GV giải thích tại sao hình bên không là khối đa diện.
Cho HS nhắc lại các phép biến hình trong mặt phẳng đã học ở lớp 11.
GV giảng các phép biến hình trong không gian cho HS nắm.
GV cần nhấn mạnh việc đối xứng qua đường thẳng D phải dựng mặt phẳng (P) chứa M và vuông góc với đường thẳng D.
GV vẽ một khối chóp và thực hiện hai phép dời hình cho HS xem.
I. Khối Lăng Trụ và Khối Chóp :
Khối lập phương là phần không gian được giới hạn bởi một hình lập phương kể cả hình lập phương ấy.
Khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ ấy.
Khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy.
Tên của lăng trụ hay khối chóp được đặt theo tên của hình lăng trụ hay hình chóp giới hạn nó.
Đỉnh , cạnh , mặt , mặt bên , mặt đáy , cạnh bên , cạnh đáy , . . của hình lăng trụ ( hình chóp) cũng được gọi cho khối lăng trụ ( khối chóp )tương ứng.
Điểm không thuộc khối lăng trụ gọi là điểm ngoài của khối lăng trụ. 
Điểm thuộc khối lăng trụ nhưng không thuộc hình lăng trụ tương ứng với khối lăng trụ đó gọi là điểm ngoài của khối lăng trụ. 
Ví dụ : Kim tự tháp ở Ai Cập chúng có hình dáng là các khối đa diện đều.
II. Khái niệm về hình đa diện và khối đa diện :
Khái niệm về hình đa diện :
Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Ví dụ : Hình sau đây là một hình đa diện:
Khái niệm về khối đa diện :
 Khối đa diện là phần không gian đực giới hạn bởi một hình đa diện , kể cả hình đa diện đó.
 Ví dụ : Các hình sau là các khối đa diện : 
 Các hình sau không là khối đa diện :
III. Hai đa diện bằng nhau:
Phép dời hình trong không gian : Trong không gian , quy tắc đặt tương ứng mỗi điểm M với điểm M’xác định duy nhất được gọi là phép biến hình trong không gian. Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tuỳ ý.
Các phép dời hình :
Phép tịnh tiến theo véctơ : 
 M M’ 
 	 Biến mỗi điểm M thành M’sao cho : 
Phép đối xứng qua mặt phẳng (P):
·
·
·
 M
 P
 M’
	Biến mỗi điểm thuộc (P) thành chính nó.
	Biến mỗi điểm M Ï (P) thành điểm M’ sao cho (P) là mặt phẳng trung trực của đoạn MM’
Phép đối xứng tâm O :
·
 M’
 O
·
·
 M
	Biến điểm O thành chính nó.
	Biến mỗi điểm M khác O thành điểm M’ sao cho O là trung điểm MM’
Phép đối xứng qua đường thẳng D :
	 D	
·
·
 M M’ 
 P
	Biến mọi điểm thuộc D thành chính nó.
	Biến mỗi điểm M không thuộc D thành điểm M’ sao cho D là đường trung trực của MM’
Nhận xét :
	Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.
	Phép dời hình biến đa diện (H) thành đa diện (H’) , biến đỉnh , cạnh , mặt của đa diện (H) thành đỉnh , cạnh , mặt tương ứng của hình (H’).
Hai hình bằng nhau : Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
Đặc biệt : Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.
IV. Phân chia và lắp ghép các khối đa diện :
Củng cố : 
	1 . Nhắc lại các khái niệm. 
	2. Phân chia một khối chóp S.ABCD thành ba khối có đỉnh là các đỉnh của khối chóp ban đầu không ?
Dặn dò : Về nhà học bài và làm đầy đủ bài tập trong SGK.