Giáo án Giải tích 12 NC - Tiết 4: Cực trị của hàm số

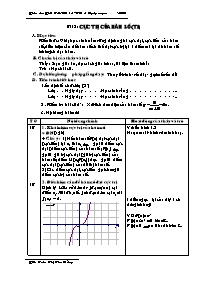
Bài 2: CựC TRị CủA HàM Số (t1)
 A. Mục tiêu 
Kiến thức: Giúp học sinh nắm vững định nghĩa cực đại, cực tiểu của hàm số, điều kiện cần để hàm số có thể đạt cực trị tại 1 điểm mà tại đó hàm số không có đạo hàm .
 B. Chuẩn bị của thầy và trò 
Thầy : Soạn giáo án, đọc sách giáo khoa, tài liệu tham khảo 
Trò : Học bài cũ.
 C. Dự kiến phương pháp giảng dạy: Thuyết trình-vấn đáp - gợi mở vấn đề
 D. Tiến trình tiết học 
1.ổn định tổ chức lớp (2’)
LớpNgày dạyHọc sinh vắng..
LớpNgày dạyHọc sinh vắng..
2 . Kiểm tra bài cũ 5’: Xét tích đơn điệu của hàm số .
3. Nội dung bài mới 
T G
Nội dung chính
Hoạt động của thầy và trò
10’
10’
15’
3’
1. Khái niệm cực trị của hàm số
+ ĐN (sgk)
+ Chú ý: 1) Nếu hàm số f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số ; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số; điểm M(x0;f(x0)) được gọi là điểm cực đại (cực tiểu) của đồ thị hàm số.
2) Các điểm cực đại, cực tiểu gọi chung là điểm cực trị của hàm số. 
2. Điều kiện cần để hàm số đạt cực trị 
Định lý 1.Giả sử hàm hs f đạt cực trị tại điểm x0. Khi đó, nếu f có đạo hàm tại x0 thì f’(x0) = 0.
Chú ý: 
Một hàm số chỉ có thể đạt cực trị tại 1 điểm mà tại đó đạo hàm của hs bằng 0 hoặc không xác định.
3. Điều kiện đủ để hàm số đạt cực trị:
Định lý 2: 
Giả sử hàm số f liên tục trên khoảng (a;b) chứa điểm x0 và có đạo hàm trên khoảng (a;x0) và (x0; b). Khi đó
Nếu f’(x) 0 với mọi thì hàm số f đạt cực tiểu tại điểm x0 . 
Nếu f’(x) > 0 với mọi và f’(x) < 0 với mọi thì hàm số f đạt cực đại tại điểm x0 . 
Định lý 2 được viết gọn trong 2 bbt:
x
a	x0	b
f’(x)
	-	+
f(x)
 CT
x
a	x0	b
f’(x)
	+	-
f(x)
	CĐ
IV. Củng cố:
-Hs nắm được k/n về cực trị, đk cần để hàm số có cực trị.
V. Công việc về nhà:
Học thuộc đn và điều kiện cần để hàm số có cực trị.
Vẽ sẵn hình 1.2
Hs quan sát hình vẽ minh hoạ.
? điều ngược lại của đlý 1 có đúng không?
VD: f(x)= x3 
f’(x) =3x2 0 .
f’(x) =0 x= 0 hs đb trên R.
Cho hàm số f(x) = hàm số không có đạo hàm tại điểm x=0
Nhưng : hs trên xác định trên R và vì f(0) =0 , nên hs đạt cực tiểu tại x=0
? Như vậy 1 hs có thể đạt cực trị tại những điểm nào?
Nếu f’(x) >0 thì so sánh f(x) và f(x0) ?
Nhận xét và chữ kí của tổ trưởng: