Giáo án Giải tích 12 - Chương I: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số (20 tiết)

Chương I
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
(20tiết)
§1. SỰ ĐỒNG BIẾN VÀ NGHỊCH BIẾN CỦA HÀM SỐ (2t)
Tiết: 1 – 2
I/. Mục đích và yêu cầu:
- Rèn cho HS kiến thức và kĩ năng: 
+ Biết tính đơn điệu của hàm số
+ Biết mối liên hệ giữa sự đồng biến, nghịch bến của hàm số và dấu đạo hàm cấp một của nó
+ Biết quy tắc xét tính đơn điệu của hàm số
+ Biết cách xét sự đồng biến, nghịch biến trên một khoảng dựa vào dấu đạo hàm cấp một của nó.
II/. Phương pháp:
Nêu vấn đề, giải quyết vấn đề, đàm thoại và hoạt động nhóm
Nội dung bài
Hoạt động của GV
Hoạt động của HS
§1. SỰ ĐỒNG BIẾN VÀ NGHỊCH BIẾN 
 CỦA HÀM SỐ
I/. Tính đơn điệu của hàm số:
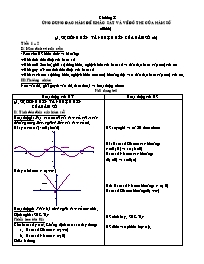
Hoạt động1: Dựa vào đồ thị của hàm số, chỉ ra các khoảng đồng biến, nghịch biến của hàm số đó.
H1: y = cosx / [ -p/2 ; 3p/ 2]
H2: y = |x| trên (- ¥; +¥ ) 
Hoạt động2: Nhắc lại định nghĩa hàm số đơn điệu.
Định nghĩa: SGK Tr.4
Phiếu học tập 01:
Cho hàm số y = x2. Khẳng định nào sau đây đúng:
Hàm số Đb trên (- ¥; +¥)
Hàm số Nb trên (- ¥; 0)
Đ/A: b đúng
Nhận xét: SGK Tr.5
Hoạt động3: Mối liên hệ giữa tính đơn điệu và dấu của đạo hàm.
¨Cho HS làm theo nhóm HĐ2 trong sgk/ 5.
Kết quả:
y’ > 0 trong khoảng nào thì hàm số Đb trên khoảng đó và y’ < 0 trong khoảng nào thì hàm số Nb trên khoảng đó.
Định lí: sgk/ 6: HS đọc
Ghi nhớ:
Trên khoảng K
 + f’(x) > 0 thì f(x) đồng biến
 + f’(x) < 0 thì f(x) nghịch biến
 + f’(x) = 0 "x Ỵ K thì f(x) không đổi trên K
Ví dụ: Tìm các khoảng đơn điệu của hàm số: y = 1 – 2x4 
Giải :
Ta có: D = R, y’ = - 8x3. Bảng biến thiên
 x - ¥ 0 + ¥ 
 y’ + 0 - 
 y 1
 - ¥ - ¥ 
Vậy: Hàm số Đb trên (- ¥ ; 0) và Nb trên 
(0 ; + ¥) 
Hoạt động4: Xét xem khẳng định ngược lại của định lí trên có đúng hay không ? đưa ra chú ý.
Cho HS làm HĐ3 sgk/ 7.
Hàm số Đb trên R và y’chưachắc > 0 trên R
y’ = 3x2 > 0 " x ¹ 0
Chú ý: Nếu không bổ sung giả thiết thì ngược lại của định lí là không đúng.
Ta có định lí mở rộng: sgk/ 7
Ví dụ: Tìm các khoảng đơn điệu của hàm số: y = 2x3 – 6x2 + 6x – 10
Giải :
Ta có: D = R, y’ = 6(x - 1)2 ³ 0 " x Ỵ R
Nên hàm số đã cho luôn luôn Đb trên R
II/. Quy tác xét tính đơn điệu của hàm số:
Hoạt động5: Hình thành quy tác 
 ? Qua các ví dụ trên hãy cho biết cách xét tính đơn điệu của một hàm số ?
Quy tác: SGK/ 8
Ghi nhớ
Tìm tập xác định
Tính đạo hàm f’(x) và tìm các điểm mà tại đó đạo hàm = 0 hoặc không XĐ
Lập bảng biến thiên
Kết luận
Hoạt động6: Luyện tập và củng cố
Bài 1: BT1/ 9 sgk
Chia lớp thành 4 nhóm, mỗi nhóm làm 1 câu
Kết quả:
Đb trên (-¥; 3/2), Nb trên (3/2; +¥) 
Đb trên (-¥;- 7), (1; +¥); Nb trên (-7;1) 
Đb trên (-1;0), (1;+¥); 
 Nb trên (-¥;- 1), (0 ; 1)
Đb trên (0 ; 2/ 3); 
 NB trên (-¥; 0), (2/ 3; + ¥)
Bài 2: BT 2a,c/ 10 sgk
Chia lớp thành 2 nhóm, mỗi nhóm làm 1 câu
Kết quả:
Ta có: y’ = > 0 " x ¹ 1 nên hàm Đb trên các khoảng: (-¥ ; 1), (1 ; + ¥)
Tập xác định: D =(- ¥ ; - 4 ] È [5 ; + ¥) và y’ = 
 Khi x Ỵ ( -¥; - 4) thì y’ < 0 
và khi x Ỵ (5 ; + ¥) thì y’ >0
Vậy hàm số Đb trên (5 ; + ¥); NB/ ( -¥; - 4) 
Þ Các bài tập còn lại HS tự làm.
Phiếu học tập 02: 
Câu1: 
HS y = f(x) Đb trên K Û "x1, x2Ỵ K, 
 x1 < x2 Þ f(x1) .f(x2) 
HS đồng biến hoặc nghịch biến trên K được gọi chung là .trên khoảng đó
f(x) Nb trên K Û .. 0 "x1, x2Ỵ K, (x1¹ x2)
Nếu hàm số Đb trên K thì đồ thị của nó. từ trái sang phải
Câu2: Hàm số nào sau đây là hàm số Đb trên R ?
y = (x2 - 1)2 – 3x + 2; b. y = 
c. y = ; d. y = tanx
Kết quả: câu b.
HS suy nghĩ và trả lời theo nhóm
H1: Hàm số Đb trên các khoảng:
(-p/2 ; 0 ) và (p ; 3p/2)
Hàm số Nb trên các khoảng:
(0; p/2) và (p/2; p) 
H2: Hàm số Nb trên khoảng: (- ¥; 0)
Hàm số Đb trên khoảng:(0; +¥ )
HS trình bày. SGK Tr.4
HS điền vào phiếu học tập.
HS sử dụng giấy để trình bày kết quả
HS ghi nhớ.
HS làm theo nhóm như VD1/ 6
1 HS đọc định lí mở rộng
HS làm theo nhóm như bài VD2 / 7
HS trả lời
HS ghi nhớ
HS làm theo nhóm, đại diện các nhóm trình bày.
HS làm theo nhóm, đại diện các nhóm trình bày.
HS làm theo nhóm.
Củng cố và dặn dò: về nhà xem lại các dạng toán đã giải và làm các bài tập còn lại
-----–—-----
Tiết 3,4:
§2. CỰC TRỊ CỦA HÀM SỐ (3tiết)
1/. Mục đích – yêu cầu:
- Rèn cho HS các kiến thức và các kĩ năng:
+ Biết các khái niệm điểm cực đại, điểm cực tiểu, điểm cực trị của hàm số.
+ Biết các điều kiện đủ để có điểm cực trị của hàm số.
+ Biết cách tìm điểm cực trị của hàm số
2/. Phương pháp: Nêu vấn đề - giải quyết vấn đề, sử dụng hoạt động nhóm và đàm thoại
3/. Kiểm tra bài cũ: Nêu quy tắc xét tính đơn điệu của hàm số ?
 Aùp dụng: y = x2 – 2x - 3
Đ/A: Hàm số Đb trên (1 ; + ¥) và Nb trên (-¥; 1)
Nội dung bài mới
Hoạt động của GV
Hoạt động của HS
§2. CỰC TRỊ CỦA HÀM SỐ
I/. Khái niệm cực đại, cực tiểu:
Hoạt động1: Hình thành khái niệm
Cho HS làm hoạt động 1 trong SGK/ 13
Kết quả: 
GTLN là y = 1 tại x = 0 và không có GTNN
GTLN trên (1/ 2; 3/ 2) là y = 4/ 3 tại 
 x = 1 và GTNN trên (3/2; 4)là y = 0 tại x = 3
¨ Ta có:
 a. y = - x2 + 1
Þ y’ = - 2x 0 với x Ỵ (-¥ ; 0) nên hàm số Đb / (-¥ ; 0) 
và Nb / (0 ; +¥)
b. y = Þ y’ = x2 – 4x + 3 nên
hàm số Đb / các khoảng (-¥; 1), (3 ; + ¥) và Nb/ (1;3)
¨ Điền dấu đạo hàm vào bảng biến thiên(SGK).
Định nghĩa: SGK/13
GV giải thích khoảng lân cận của điểm x0 .
Chú ý: Sgk/ 14
+ x0 : Đgl điểm CĐ(điểm CT) của hàm số
+ f(x0): Đgl giá trị CĐ(GTCT) của hàm số
Kí hiệu là: fCĐ(fCT)
+ M(x0; f(x0)): Đgl điểm CĐ(điểm CT ) của đồ thị hàm số.
+ Điểm CĐ và điểm CT được gọi chung là điểm cực trị. Giá trị CĐ(GTCT) còn gọi là CĐ(CT) và được gọi chung là cực trị của hàm số.
+. Nếu hàm số có đạo hàm và đạt CĐ hoặc đạt CT tại điểm x0 thì f ’(x0) = 0
¨ Tổ chức cho HS làm HĐ2/ 14 Sgk
GV: Ta có: y = f(x) CĐ tại điểm x0 nên 
Þ f(x0 + Dx) – f(x0) ? < 0
+ Với Dx > 0 Þ ? < 0
Lấy giới hạn vế phải, ta được:
f ’(x0) = ? £ 0 (1)
+ Với Dx 0
Lấy giới hạn vế trái, ta được:
f ’(x0) = ? ³ 0 (2)
Từ (1), (2) ta có: f ’(x0) = 0
II/. Điều kiện đủ để hàm số có cực trị:
Hoạt động 2: Hình thành định lí
Cho HS làm HĐ3/ 14 Sgk
Hình 8 có cực trị
Nếu y’ > 0 hoặc y’ < 0 thì hàm số không có cực trị; nếu y’ là một biểu thức chứa x và đổi dấu khi đi qua điểm x0 thì có cực trị.
¨Định lí: Sgk/ 14
Ví dụ: Tìm các điểm cực trị của các hàm số sau:
y = - 2x2 + 3
y = x3 – 2x2 + 3x + 5
y = ; d. y = 
Giải: Chia HS làm 4 nhóm mỗi nhóm làm 1 câu.
Kết quả:
y’ = - 4x, y’ = 0 Û x = 0, vậy hàm số đạt CĐ tại điểm x = 0 và không có ĐCT
y’ = x2 – 4x + 3; y’ = 0 Û x = 1; x = 3 
BBT: x - ¥ 1 3 + ¥
 y’ + 0 - 0 +
 y 5 
 Vậy hàm số đạt CĐ tại x = 1 và đạt CT tại 
x = 3 
c. ta có: D = R\ {1}, y’ = > 0 "x ¹ 1
nên hàm số không có cực trị.
d. Ta có: D = R, y’ = 
 y’ = 0 Û x = ± 1 đổi dấu khi đi qua điểm đó nên có cực trị và hàm số đạt CĐ tại x = 1, đạt CT tại x = - 1
III/. Quy tắc tìm cửc trị:
1/. Quy tắc I:
Từ các VD trên cho HS nhắc lại các bước làm ?
Quy tắc I: Sgk/ 16
GV hướng dẫn Cho HS làm HĐ5 / 16 
Kết quả: y’ = 3(x2 - 1), y’ = 0 Û x = ± 1 
Hàm số đạt CĐ tại x = - 1 và đạt CT tại x = 1 
Định lí 2: Sgk/ 16, cho HS đọc 
2/. Quy tắc II: 
Ví dụ: Cho hàm số y = x4 + 2x2 + 6
Tìm tập xđ ?
Tính y’ = ?, y’ = 0 Û x = ? x0
Tính y’’ = ? và y’’(x0) = ?
Dựa vào định lí 2 Þ cực trị 
Giải : Cho HS làm theo nhóm
Þ Quy tắc II: Sgk/ 17
1 Hs đọc ĐN
1HS đọc chú ý
HS ghi nhớ
HS suy nghĩ và làm theo sự gọi ý của GV.
HS làm theo nhóm
HS làm theo nhóm và đại diện các nhóm trình bày.
HS đọc quy tắc I Sgk / 16 và ghi nhớ
HS làm theo nhóm.
HS tính toán theo yêu cầu của GV.
Củng cố và dặn dò: 
Các em về nhà cần: Học thuộc định nghĩa cực trị, định lí 1, 2 và các quy tắc tìm cực trị của hàm số. Làm bài tập: 1,2,4,6 sgk / 18 và đọc trước bài 3 / 19 sgk.
BÀI TẬP: (1tiết)
Tiết 5:
Rèn cho HS các kĩ năng giải toán dạng: Tìm các điểm cực trị của hàm số và xác định tham số m thoả điều kiện cho trước.
Nội dung bài
Hoạt động của GV
Hoạt động của HS
Bài 1/ 18: Sgk
+ Mời 1 HS phát biểu quy tắc I ?
+ Mời 3 HS lên làm bài 1a,c,e
ØKết quả:
1a. y’ = 6x2 + 6x - 36
Hàm số đạt cực đại tại x = - 3 và yCĐ= 71
Hàm số đạt cực tiểu tại x = 2 và yCT = - 54
1c. y’ = , TXĐ: D = R\ {0}
Hàm số đạt cực đại tại x = - 1 và yCĐ= - 2
Hàm số đạt cực tiểu tại x = 1 và yCT = 2
1e. y’ = , D = R vì x2 – x + 1 > 0
Hàm số đạt cực tiểu tại x = 1/ 2 và yCT = và hàm số không có cực đại
Bài 2/ 18: Sgk
+ Mời 1 HS phát biểu quy tắc II ?
+ Mời 2 HS lên làm bài 1a,c
ØKết quả:
2a. y’ = 4x(x2 - 1); y’’ = 12x2 – 4
y’ = 0 Û x = 0, x = ± 1
y’’(0) = - 4 < 0 Þ h/ số đạt cực đại tại x = 0
y’’(±1) = 8 > 0Þ h/ số đạt cực tiểu tại x = ± 1
2c. ta có: y = sinx + cosx = 
y’ = ; y’’ = - 
y’ = 0 Û x = , k Ỵ Z
y’’() = - = - nếu k chẵn và = nếu k lẻ
Vậy h/số đạt CĐ tại các điểm x = và đạt CT tại các điểm x = ,k Ỵ Z
Bài 4/ 18: Sgk
+. HD cho HS làm theo nhóm
+. Hàm số có 1 CĐ và 1 CT khi phương trình 
y’ = 0 có hai nghiệm phân biệt và đổi dấu khi đi qua các nghiệm đó.
ØKết quả:
D’ = m2 + 6 > 0 "m Ỵ R Þ đpcm
Bài 6/ 18: Sgk
GV hướng dẫn cho HS tự làm
ØKết quả: y’ = 
Nếu h/số đạt CĐ tại x = 2 thì y’(2) = 0
Û m2 + 4m + 3 = 0 Û 
m = - 1 không thoả ĐK, chỉ có m = - 3 thoả
¨Các bài tập còn lại HS tự làm.
HS trình bày
HS trình bày và đánh giá
Đại diện các nhóm trình bày
Củng cố và dặn dò:
Học thuộc và vận dụng tốt quy tắc I và quy tắc II.
§3. GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
(3tiết)
Tiết : 6, 7
1/. Mục đích – yêu cầu:
+. Nắm vững khái niệm GTLN – GTNN; Quy tắc tìm GTLN – GTNN.
+. Rèn cho HS các kĩ năng: Tính được các GTLN- GTNN trên một đoạn của một hàm số thường gặp; Phương pháp tính GTLN – GTNN của một hàm số trên một đoạn, trên một khoảng.
2/. Phương pháp: Đàm thoại(Hoạt động nhóm), gợi mở và giải quyết vấn đề
3/. Tiến trình bài học:
+. Ổn định lớp:
+. Kiểm tra bài cũ: (Lồng với bài dạy)
+. Bài mới:
Nội dung bài mới
Hoạt động của GV
Hoạt động của HS
§3. GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ 
 NHỎ NHẤT CỦA HÀM SỐ
Ví dụ1: Tìm cực trị của hàm số: y = x –  ... nghịch biến trên các khoảng (- ¥; 0)
 và ( 2 ; + ¥); đồng biến trên (0; 2)
 +. Cực trị:
 H/số đạt CĐ tại x = 2; yCĐ = 0
 H/số đạt CT tại x = 0 ; yCT = - 4
 +. Giới hạn tại vô cực:
 = + ¥ ; = - ¥
 +. BBT:
 x - ¥ 0 2 + ¥ 
 y’ - 0 + 0 -
 y +¥ 0
 - 4 - ¥
- Đồ thị:
Ta có: - x3 + 3x2 – 4 = 0 Û 
Đồ thị cắt trục ox tại (2 ; 0), (- 1 ; 0) và cắt trục tung tại (0 ; - 4)
NX: Đồ thị nhận điểm I(1 ; - 2) làm tâm đối xứng.
Ví dụ2: Khảo sát sự biến thiên và vẽ đồ thị của h/ số y = x3 - x2 + x + 1
Giải: Tổ chức cho HS làm theo nhóm 
Đồ thị như hình sau:
¨ Dạng của đồ thị hàm số bậc ba: 
y = ax3 + bx2 + cx + d (a ¹ 0): (Sgk/ 35)
2/. Hàm số y = ax4 + bx2 + c (a ¹ 0):
Ví dụ3: Khảo sát sự biến thiên và vẽ đồ thị của h/ số y = x4 – 2x2 – 3
Giải: Tổ chức cho HS làm theo nhóm 
- TXĐ: D = R
- Sự biến thiên:
 + Chiều biến thiên:
 y’ = 4x3 – 4x = 4x(x2 - 1)
 y’ = 0 Û 4x(x2 - 1) = 0 Û 
 Trên các khoảng (- 1; 0), (1 ; +): H/số 
 Đbiến và Nbiến trên (-¥; - 1), (0 ; 1)
 + Cực trị:
 H/số đạt CĐ tại x = 0; yCĐ = - 3
 H/số đạt CT tại x =± 1 ; yCT = - 4
 + Giới hạn tại vô cực: = +¥
 + BBT:
 x - ¥ -1 0 1 + ¥
 y’ - 0 + 0 - 0 +
 y +¥ -3 +¥ 
 - 4 - 4
3. Đồ thị:
Đồ thị nhận trục oy làm trục đối xứng; cắt trục ox tại (; 0), (-; 0); cắt trục tung tại (0; - 3)
Ví dụ4: Khảo sát sự biến thiên và vẽ đồ thị của h/ số y = - x4 + 2x2 + 3
Dựa vào đồ thị biện luận theo m số nghiệm của phương trình: - x4 + 2x2 + 3 = m
Giải: Tổ chức cho HS làm theo nhóm 
+. Đồ thị như hình sau:
+. Số nghiệm của PT là số giao điểm của đồ thị (C) và đường thẳng y = m
Dựa vào đồ thị ta có:
 - Nếu m > 4 thì PT vô nghiệm
 - Nếu 3 < m < 4 thì PT có 3 nghiệm
 - Nếu m < 3 thì PT có 2 nghiệm
 - Nếu m = 4 thì PT có 2 nghiệm
 - Nếu m = 3 thì PT có 3 nghiệm
¨ Dạng của đồ thị hàm số
y = ax4 + bx2 + c (a ¹ 0): (SGK)
3/. Hàm số y = (c ¹ 0, ad – bc ¹ 0):
Ví dụ5: Khảo sát sự biến thiên và vẽ đồ thị của h/ số y = 
Giải: Tổ chức cho HS làm theo nhóm 
TXĐ: D = R\ {- 1}
Sự biến thiên:
+. Chiều biến thiên:
y’ = < 0 "x Ỵ D Þ H/số NB trên các khoảng (- ¥; - 1), (- 1 ; + ¥) 
+. H/ số không có cực trị.
+. Tiệm cận: = + ¥ ; = - ¥
Þ Đường thẳng x = - 1 là TCĐ
Mặt khác: = - 1 Þ y = - 1 là TCN
+. BBT: 
 x - ¥ - 1 + ¥
 y’ - -
 y - 1 +¥ 
 - ¥ -1
 - Đồ thị:
Đồ thị nhận giao điểm của hai đường tiệm cận làm tâm đối xứng và đi qua các điểm:
(2 ; 0), (0 ; 2) như hình bên.
Ví dụ6: Khảo sát sự biến thiên và vẽ đồ thị của h/ số y = 
Giải: Tổ chức cho HS làm theo nhóm 
Ta có: y’ = > 0 "x Ỵ D 
Đồ thị như hình sau:
¨ Dạng đồ thị của hàm số
 y = (c ¹ 0, ad – bc ¹ 0): (Sgk / 41).
III/. SỰ TƯƠNG GIAO CỦA CÁC ĐỒ THỊ:
¨Tổ chức cho HS làm HĐ6/ 42(sgk)
ØKết quả: Hoành độ giao điểm của hai đường là nghiệm của PT: 
x2 + 2x – 3 = - x2 - x + 2 Û 2 x2 + 3x – 5 = 0
Û Þ 
Ví dụ 7: (sgk/ 42). Cmr đồ thị (C) của h/số:
y = luôn luôn cắt đường thẳng (d): 
y= m – x với mội giá trị của m.
Giải: Tổ chức cho HS làm theo nhóm 
(C) luôn cắt (d) khi PT: = m – x có nghiệm với mọi m
Thật vậy: PT Û 
Và D = m2 + 8 > 0 "m và x = - 1 không thoả PT trên Þ đpcm
Ví dụ 8: bài tập 5/ 44 (sgk)
Giải: Tổ chức cho HS làm theo nhóm tương tự như ví dụ 8 trong sgk/ 42.
a). Đồ thị của h/số y = - x3 + 3x + 1 như hình bên:
 b). Ta có: x3 – 3x + m = 0 
 Û - x3 + 3x + 1 = m + 1
Từ đồ thị ta thấy:
+ Nếu m + 1 > 3 hoặc m + 1 < -1
Û m > 2 hoặc m < - 2: PT có một nghiệm;
+ m = 2 hoặc m = - 2: PT có hai nghiệm
+ - 2 < m < 2: PT có ba nghiệm.
HS vận dụng Sgk và ghi nhớ.
HS làm theo nhóm và đại diện các nhóm trình bày.
HS làm theo 2 nhóm, đại diện các nhóm lên làm.
HS học trong Sgk
HS làm theo 2 nhóm, đại diện các nhóm lên làm.
HS làm theo 2 nhóm, đại diện các nhóm trình bày.
HS xem SGK/ 38
HS làm theo nhóm, đại diện các nhóm trình bày.
HS xem trong sgk / 41.
HS làm theo 2 nhóm và đại diện các nhóm trình bày.
HS làm theo 2 nhóm và đại diện các nhóm trình bày.
HS làm theo 2 nhóm và đại diện các nhóm trình bày.
Củng cố và dặn dò:
Các bước khảo sát h/số ? ; sự tương giao của hai đồ thị ?; xem lại các VD đã làm.
Bài tập về nhà: 1, 2,3, 6, 8, 9/ 43,44(sgk)
Xem trước bài tập và các kiến quan trọng trong chương I.
-----–—-----
BÀI TẬP: (2t); Tiết: 16,17
Rèn cho HS các kĩ năng giải dạng toán: Khảo sát và vẽ đồ thị của các hàm số và các bài toán liên quan.
Kiểm tra bài cũ: Các bước khảo sát hàm số ? và phương trình tiếp tuyến của đồ thị hàm số tại điểm M0(x0 ; y0) ?
Nội dung bài tập.
Hoạt động của GV
Hoạt động của HS
Bài 1/ 43(sgk):
Mời 02 HS lên làm.
ØKết quả:
a). y = 2 + 3x – x3 ; 
+ D = R
+ y’ = 3(1 – x2) 
y’ = 0 Û x = ± 1; 
+ 
+ BBT:
 x - ¥ -1 1 + ¥ 
 y’ - 0 + 0 - 
 y +¥ 4
 0 - ¥
H/s Đb trên (- 1 ; 1); Nb trên các khoảng
(- ¥ ; - 1), (1 ; + ¥) và CĐ tại x = 1 Þ yCĐ = 4
CT tại x = - 1 Þ yCT = 0
+ Đồ thị: đồ thị như hình bên
b). y = x3 + 4x2 + 4x
Tương tự như trên ta có đồ thị như sau:
Bài 2/ 43(sgk): Mời 02 HS lên làm câu b ;d.
ØKết quả:
Làm tương tự như bài 1 ta có các đồ thị như sau:
b). y = x4 – 2x2 + 2
Ta có BBT:
 x -¥ -1 0 1 +¥
 y’ - 0 + 0 - 0 +
 y +¥	 1 2 1 +¥ 
d). y = - 2x2 – x4 + 3
Đồ thị như hình bên
Bài 3/ 43(sgk): Mời 02 HS lên làm câu a ;b.
a). y = ; 
+ D = R\ {1}
+ y’ = < 0 "xỴ D
H/s Nb trên (-¥; 1); (1 ; + ¥); không có ctrị
+ Tiệm cận:
Vì = - ¥ ; = + ¥
Nên x = 1 là đường TCĐ
Mặt khác: = 1 nên y = 1 là TCN
+ BBT: x -¥ 1 +¥
 y’ - -
 1 +¥
 -¥ 1
+ Đồ thị: như hình bên
b). y = 
Ta có: y’ = > 0 "x Ỵ D
Làm tương tự ta có đồ thị như hình bên.
Bài 8/ 44(sgk): HD cho HS làm theo nhóm
ØKết quả: y = x3 + (m + 3)x2 + 1 – m
a). Ta có: y’ = 3x2 + 2(m + 3)x
và y’’ = 6x + 2(m + 3)
H/s đạt CĐ tại x = - 1 Û 
Û 
b). Đồ thị cắt trục hoành tại x = - 2 
Û y(-2) = 0 Û m = 
Bài 6/ 44(sgk): HD cho HS làm theo nhóm.
 y = 
a). D= R \ {- }; y’ = > 0 "mỴ R 
Þ Đpcm
b). Phương trình tiệm cận đứng của đồ thị là: x = - 
TCĐ đi qua điểm A(- 1; ) -1 = - Û m = 2
c). Với m = 2 thì y = (HS tự làm).
02 HS lên bảng làm câu a, b.
02 HS trình bày trên bảng câu b, d.
02 HS lên bảng làm câu a, b.
HS làm theo nhóm và đại diện các nhóm lên trình bày.
HS làm theo nhóm và đại diện các nhóm lên trình bày.
Củng cố và dặn dò:
Về nhà xem lại các bài và các câu tương tự chưa giải và xem lại các phần quan trọng chương
Bài tập ôn chương: 1, 2, 3, 4, 7, 9, 11/ 45, 46.
-----–—-----
ƠN TẬP CHƯƠNG I
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT 
VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ 
I. Mục tiêu: 
+ Kiến thức: Củng cố lại những kiến thức quan trọng của chương I như các vấn đề đồng biến, nghịch biến, cực đại, cực tiểu, giá trị lớn nhất, giá trị nhỏ nhất, tiệm cận. Khảo sát thành thạo một số hàm số thường gặp và giải một số bài tốn liên quan.
+ Kĩ năng: Rèn luyện cho HS kĩ năng vận dụng các dấu hiệu về đồng biến, nghịch biến, cực trị tiệm cận trong các bài tốn cụ thể
	Vận dụng thành thạo sơ đồ khảo sát sự biến thiên và vẽ đồ thị hàm số.
	Rèn luyện phương pháp giải một số bài tốn liên quan như viết phương trình tiếp tuyến, biện luận số nghiệm của phương trình bằng phương pháp đồ thị.
+ Tư duy và thái độ:
	- Rèn luyện tư duy logic
	- Rèn luyện thái độ: Cẩn thận, nghiêm túc.
II. Chuẩn bị của giáo viên và học sinh:
1) Giáo viên: Giáo án, bảng phụ.
2) Học sinh: Ơn lại lý thuyết cơ bản trọng tâm của chương và chuẩn bị bài tập chương.
III. Phương pháp dạy học: 
	Gợi mở, nêu vấn đề và giải quyết vấn đề .
IV. Tiến trình bài học: 
1) Ổn định tổ chức:
2) Kiểm tra bài cũ: (5’)
Câu hỏi 1: Nêu sơ đồ bài tốn khảo sát sự biến thiên và vẽ đồ thị hàm số ?
Câu hỏi 2: Nêu phương pháp viết phương trình tiếp tuyến ?.
3) Bài mới: 
Hoạt động 1: 
Hoạt động của giáo viên 
Hoạt động của học sinh 
Ghi bảng, trình chiếu
GV: gọi 2 HS giải
GV gọi 2 HS nhận xét và đánh giá bài làm từng học sinh
. 1HS nêu điều kiện để H/SĐBNB và tìm khoảng đơn điệu của H/S y = -x3 + 2x2 – x + 7.
. 1HS nêu qui tắc xét tính đơn điệu của H/S và tìm khoảng đơn điệu của H/S y = .
Bài 1 (Trang 45)
Hoạt động 2: 
Hoạt động của giáo viên 
Hoạt động của học sinh 
Ghi bảng, trình chiếu
GV: gọi 2 HS giải
GV gọi 2 HS nhận xét và đánh giá bài làm từng học sinh
. 1HS nêu qui tắc 1 về tìm cực trị của H/S nhờ đạo hàm và áp dụng tìm các điểm cực trị của H/S.
y = x4 – 2x2 + 2 
. 1HS nêu qui tắc 2 về tìm cực trị của H/S nhờ đạo hàm và áp dụng tìm các điểm cực trị của H/S 
 y = x4 – 2x2 + 2
Bài 2 (Trang 45)
Hoạt động 3: 
Hoạt động của giáo viên 
Hoạt động của học sinh 
Ghi bảng, trình chiếu
GV: gọi HS khảo sát sự biến thiên và vẽ đồ thị (C) của y = x3 + 3x2 + 1
GV nhận xét và đánh giá.
GV: yêu cầu HS nhắc lại tính chất đồ thị y = C
GV dẫn dắt cách giải câub. Nghiệm của PT:
x3 + 3x2 + 1 = (*)
là số hồnh độ giao điểm của (C) và đt y = 
GV yêu cầu HS nêu điểm cực đại, cực tiểu của (C).
GV yêu cầu HS viết pt đường thẳng đi qua 2 điểm.
GV nhận xét và đánh giá
GV gọi 2 HS nhận xét và đánh giá bài làm từng học sinh
HS khảo sát và vẽ đồ thị.
HS nghe rõ câu hỏi và trả lời.
HS biện luận số nghiệm của pt (*)
HS nêu toạ độ điểm cực đại và điểm cực tiểu của (C).
HS viết pt đường thẳng theo yêu cầu.
Bài 7 (Trang 45)
b) Dựa vào (C), biện luận số nghiệm của pt : 
x3 + 3x2 + 1 = 
c) Viết pt đường thẳng đi qua điểm cực đại và điểm cực tiểu của (C).
ĐCĐ (-2 ; 5)
ĐCT (0; 1)
PT cần tìm: 
y = - 2x + 1
Hoạt động 4: 
Hoạt động của giáo viên 
Hoạt động của học sinh 
Ghi bảng, trình chiếu
a) 
GV gọi HS giải câu a
GV gọi HS nhận xét và đánh giá.
b) GV gọi HS giải câu b
GV gọi HS nhận xét và đánh giá.
c) GV hướng dẫn HS giải.
- HS khảo sát sự biến thiên và vẽ đồ thị (C) của H/S y = 
- HS chứng minh
- HS giải theo hướng dẫn
Bài 11: Trang 46 
a). y’ = < 0
b). PT hồnh độ giao điểm: = 2x + m
Û
Thoả với " mỴ R
c).Ta cĩ điểm N(x1;2x1+m)
và M(x2 ; 2x2+m)
MN2 = (x2 – x1)2 + (y2 – y1)2
= 5(x2 – x1)2 
= 5[(x1 + x2)2 - 4 x1 x2] 
= 5[ - 2(m - 3)]
= [(m - 3)2 + 16]
Û MN = 
Đẳng thức xảy ra khi m = 3
Vậy min(MN) = khi m=3
4) Củng cố tồn bài: (5’)
	Giáo viên ra câu hỏi trắc nghiệm ở bảng phụ và học sinh trả lời.
5) Hướng dẫn học sinh giải các bài tập cịn lại của phần ơn chương.
V/ PHỤ LỤC:
	Bảng phụ: 
Câu 1: Số điểm cực trị của hàm số y = x3 – x + 2 là:
	A. 1	B. 0	C. 3	D. 2
Câu 2: Số đường tiệm cận của đồ thị hàm số y = là: 
	A. 1	B. 2	C. 3	D. 4
Câu 3: Hàm số y = đồng biến trên.
	A. R 	B. (-¥ ; 1) 	C. (1 ; +¥) 	D. R \ {1}
Câu 4: Tiếp tuyến tại điểm cực đại của hàm số y = x4 – 2x2 + 1.
Song song với đường thẳng x = 0
Song song với trục hồnh
Cĩ hệ số gĩc dương
Cĩ hệ số gĩc bằng 1.