Đề thi thử tốt nghiệp trung học phổ thông môn Toán 12

ĐỀ THI THỬ TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG
Thời gian làm bài 150 phút
Lê Duy Thiện - THPT Lang Chánh
Ngày soạn 14/3/2011
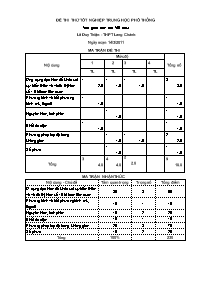
MA TRẬN ĐỀ THI
Nội dung
Mức độ
Tổng số
1
2
3
4
TL
TL
TL
TL
Ứng dụng đạo hàm để khảo sát sự biến thiên và vẽ đồ thị hàm số - Bài toán liên quan
1
2.0
1
1.0
1
1.0
3
3.0
Phương trình và bất phương trình mũ, lôgarit
1
1.0
1
1.0
Nguyên hàm, tích phân
1
1.0
1
1.0
Khối đa diện
1
1.0
1
1.0
Phương pháp toạ độ trong không gian
1
1.0
1
1.0
2
2.0
Số phức
1
1.0
1
1.0
Tổng
3
4.0
4
4.0
2
 2.0
9
10.0
MA TRẬN NHẬN THỨC
Nội dung - Chủ đề
Tầm quan trọng
Trọng số
Tổng điểm
Ứ dụng đạo hàm để khảo sát sự biến thiên và vẽ đồ thị hàm số - Bài toán liên quan
30
3
90
Phương trình và bất phương trình mũ, lôgarit
15
1
15
Nguyên hàm, tích phân
10
2
20
Khối đa diện
10
1
10
Phương pháp toạ độ trong không gian
25
3
75
Số phức
10
2
20
Tổng
100%
230
BẢNG MÔ TẢ
1. Hình thức:
	Tự luận 100%, trong đó
	- Nhận biết 3 ý (4 điểm): 40%
	- Thông hiểu 4 ý (4 điểm): 40%
	- Vận dụng 2 ý (2 điểm): 20%
2. Mô tả chi tiết:
Câu 1a. Khảo sát sự biến thiên của hàm số hữu tỷ b1/b1
Câu 1b. Xét sự tương giao giữa đồ thị hàm số với đường thẳng chứa tham số m
Câu 2a. Giải phương trình mũ (sử dụng pp đặt ẩn phụ) hoặc phương trình lôgarit
Câu 2b. Tính tích phân (sử dụng pp đặt ẩn phụ)
Câu 2c. Tìm GTLN, GTNN của hàm số.
Câu 3. Tìm diện tích của mặt cầu ngoại tiếp hình chóp
Câu 4a1. Viết phương trình mặt phẳng đi qua ba điểm cho trước phân biệt
Câu 4a2. Tìm toạ độ hình chiếu của một điểm cho trước trên một mặt phẳng cho trước
Câu 5a. Xác định môđun, tìm phần thực, phần ảo của số phức; giải phương trình bậc hai với hệ số thực; tìm điều kiện để hai số phức bằng nhau
Câu 4b1. Xét vị trí tương đối của hai đường thẳng trong không gian
Câu 4b2. Viết phương trình mặt phẳng biết đi qua môt điểm đồng thời song song với hai đường thẳng cho trước.
Câu 5b. Xác định môđun, tìm phần thực, phần ảo của số phức; giải phương trình bậc hai với hệ số thực; tìm điều kiện để hai số phức bằng nhau
I . PHẦN CHUNG CHO TẤT CẢ THÍ SINH ( 7 điểm ) 
Câu I ( 3,0 điểm ) 
Cho hàm số có đồ thị (C)
1/ Khảo sát sự biến thiên và vẽ đồ thị (C).
2/ Tìm tất cả các giá trị của tham số m để đường thẳng (d) : y = x + m cắt đồ thị của hàm số đã cho tại hai điểm phân biệt .
Câu II ( 3,0 điểm )
	1/ Giải phương trình 
	2/ Tính tích phân sau: 
	3/ Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
y = trên .
Câu III (1,0 điểm)
Cho hình chóp tam giác đều có cạnh đáy bằng và đường cao h = 1. Hãy tính diện tích của mặt cầu ngoại tiếp hình chóp.
II. PHẦN RIÊNG (3,0 điểm)
(Thí sinh chỉ được chon một trong hai phần, phần 1 hoặc phần 2)
1. Phần 1 Chương trình chuẩn
Câu IVa (2,0 điểm) 
Trong không gian với hệ toạ độ Đề các Oxyz cho ba điểm A(1; 1; 2), B(-2; 1; -1), C(2; -2; 1).
1/ Viết phương trình mặt phẳng (ABC).
2/ Xác định toạ độ hình chiếu của điểm O trên mặt phẳng (ABC)
Câu Va (1,0 điểm) Tìm x, y biết (3x-2) + (2y+1)i = (x+1) – (y-5)i .
2. Phần 2 Chương trình nâng cao
 Câu IVb (2,0 điểm)
Trong không gian cho đường thẳng d: và đường thẳng d’:
1/ Xét vị trí tương đối của d và d’.
2/ Viết phương trình mặt phẳng đi qua điểm M(-2;-3;4) và song song với d và d’
Câu Vb (1,0 điểm). Tìm môđun của số phức z6 biết z = 3-i+(1+i)3 
.Hết.
HƯỚNG DẪN CHẤM THI THỬ TỐT NGHIỆP NĂM 2008-2009
I. Phần chung
Câu
Đáp án
Điểm
I
1
2.00
a. TXĐ: R\{2}
0.25
b.Sự biến thiên
*Giới hạn vô cực và giới hạn tại vô cực
, 
Vậy đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số khi và khi 
, 
Vậy đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số khi và khi 
* Bảng biến thiên
x
 2 
y’
 + +
y
 1 
1 
Hàm số đồng biến trên mỗi khoảng (;2) và (2; )
Đồ thị hàm số không có cực trị
x
x
1
2
O
3
3/2
c. Đồ thị 
Đồ thị hàm số cắt Oy tai 
điểm (0;3/2)
Đồ thị hàm số cắt Ox tại 
điểm (3;0)
Đồ thị hàm số nhận điểm I(2;1)
làm tâm đối xứng
0.25
0.25
0.25
0.25
0.25
0.50
I
2
1.00
Đường thẳng (d) : y = x + m cắt đồ thị hàm số tại hai điểm phân biệt khi phương trình hoành độ giao điểm có hai nghiệm phân biệt khác 2
 có hai nghiệm phân biệt
 có hai nghiệm phân biệt
0.25
0.25
0.50
II
1
1.00
Đặt 
Phương trình đã cho trở thành
Với t = 1 ta có 
Vậy phương trình đã cho có nghiệm duy nhất x =0
0.25
0.25
0.25
0.25
2. Tính tích phân sau: 
1.00
Đặt u = 2x+1 khi đó du = 2 dx
Với x = 0 thì u = 1
Với x = 1 thì u = 3
Do đó =
 =
Vậy I = 
0.25
0.25
0.25
0.25
3.
1.00
Ta có 
Khi đó y(-1) = 15, y(1) = -5, y(2) = 6
Vậy GTLN của hàm số trên đoạn [-1;2] là 15
 GTNN của hàm số trên đoạn [-1;2] là -5
0.25
0.25
0.25
0.25
III
1.00
B
A
S
M
H
N
C
I
Gọi M, N lần lượt là trung điểm của SA, BC
H là trọng tâm tam giác ABC
Vì hình chóp S.ABC đều nên SH là 
đường cao của hình chóp
Theo bài ra ta có SH = 1
AB = 
Vì tam giác ABC đều nên AN = 
AH = 
Áp dụng định lý pitago cho tam giác vuông SAH ta có SA=
Gọi I là giao của mặt trung trực SA với SH, khji đó I llà tâm mặt cầu cần tìm
Bán kính mặt cầu là SI
Xét hai tam giác đồng dạng và 
ta suy ra 
Diện tích mặt cầu cần tìm là 
0.25
0.25
0.25
0.25
IVa
1
1.00
Ta có , 
Vectơ pháp tuyến của mặt phẳng (ABC) là 
Phương trình tổng quát của mặt phẳng (ABC) là
-9(x-1) – 6(y-1) +9(z-2) = 0
Hay -3x -2y + 3z – 1 = 0
0.25
0.25
0.25
0.25
2 
1.00
Gọi d là đường thẳng đi qua điểm O và vuông góc với mặt phẳng (ABC)
Khi đó vectơ chỉ phương của d là vectơ pháp tuyến của mặt phẳng (ABC) hay 
Phương trình đường thẳng d là : 
Toạ độ hình chiếu O’ của O trên mặt phẳng (ABC) là nghiệm của hệ phương trình 
Giải ra ta được x= -3/22; y = -2/22; z= 3/22
Vậy toạ độ hình chiếu của điểm O trên mặt phẳng (ABC) là
(-3/22; -2/22; 3/22)
0.25
0.25
0.25
0.25
Va
1.00
Ta có (3x-2) + (2y+1)i = (x+1) – (y-5)i 
Vậy 
0.50
0.25
0.25
IVb
1
1.00
Đường thẳng d đi qua điểm M(2;-1;0) và có VTCP 
Đường thẳng d’ đi qua điểm M’(-2;1;2) và có VTCP 
Ta có , (1)
Suy ra = (-1).(-4)+(-2).2+7.2=14 (2)
Từ (1) và (2) ta suy ra d và d’ chéo nhau
0.25
0.25
0.25
0.25
2
1.00
Mặt phẳng đi qua điểm M(-2;-3;4) có vectơ pháp tuyến là 
Phương trình mặt phẳng cần tìm là : -1(x+2) -2( y+3) +7(z-4) = 0
Hay: –x – 2y + 7z -36 = 0
0.50
0.25
0.25
Vb
1.00
Ta có z = 3-i+(1+i)3 = 3 – i + 1 +3i + 3i2 +i3 = 1+ i
Dạng lượng giác của số phức z là 
Dạng lượng giác của số phức z6 là 
Do đó nên 
Vậy 
0.25
0.25
0.25
0.25
Chú ý: Nếu thí sinh có cách giải đúng, cách giải khác với đáp án, thì người chấm cho điểm theo số điểm quy định dành cho câu (hay phần) đó.