Đề tham khảo thi học kì I Toán lớp 12 (Đề 12)

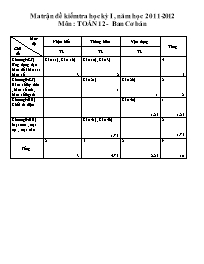
Ma trận đề kiểm tra học kỳ I , năm học 2011-2012
Môn : TOÁN 12 - Ban Cơ bản
Mức độ
Nhận biết
Thông hiểu
Vận dụng
Tổng
Chủ đề
TL
TL
TL
ChươngI:(GT)
Ứng dụng đạo hàm để khảo sát hàm số
Câu 1a) , Câu 1b)
Câu 1c) , Câu 3)
4
5
3
2
ChươngII:(GT)
Hàm số lũy thừa , hàm số mũ , hàm số lôgarit
Câu 2a)
1
Câu 2b)
2
2
1
ChươngI:(HH)
Khối đa diện
Câu 4c)
1
1.25
1.25
ChươngII:(HH)
Mặt nón , mặt trụ , mặt cầu
Câu 4a) , Câu 4b)
2
1.75
1.75
Tổng
2
5
2
9
10
3
4.75
2.25
Sở GD-ĐT Bình Định Đề kiểm tra học kỳ I , năm học: 2011-2012
Trường THPT An Lương Môn: Toán - Lớp12 - Ban: Cơ Bản
 Thời gian làm bài: 90 phút ( không kể phát đề )
Câu 1: (4đ) Cho hàm số có đồ thị (C).
Khảo sát sự biến thiên và vẽ đồ thị (C). 
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 1. 
Dựa vào đồ thị (C), hãy biện luận theo m số nghiệm của phương trình: 
Câu 2 (2đ) Giải phương trình và bất phương trình sau :
 a) 
 b) 
Câu 3: (1đ) Tính giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: 
 	trên đoạn [0;2] 
Câu 4: (3đ) Thiết diện qua trục của một hình nón là một tam giác SAB vuông cân tại S có cạnh góc vuông bằng 6 cm. 
Tính diện tích xung quanh và diện tích toàn phần của hình nón.
Tính thể tích của khối nón. 
Một thiết diện SAC qua đỉnh S tạo với đáy một góc 600. Tính diện tích của thiết diện SAC. 
 ----------------------------
TRƯỜNG THPT AN LƯƠNG ĐÁP ÁN
 ĐỀ KIỂM TRA HỌC KỲ 1, năm học: 2011-2012 
 TOÁN 12 - BAN CÓ BẢN
Học sinh làm cách khác đúng vẫn cho điểm tối đa
STT
NỘI DUNG 
THANG ĐIỂM
CÂU 1
( 4đ )
a) ( 2đ ) TXĐ : D = R
y/ = -3x2 + 6x
y/ = 0 Û -3x2 + 6x = 0 Û 
 BBT :
x
- ¥ 0 2 + ¥
y’
 - 0 + 0 -
y
+ ¥ -1 3 
 CT CĐ - ¥
Đồ thị : 
3
b) ( 1đ ) Ta có : x0 = 1 Þ y0 = 1
y/ = -3x2 + 6x Þ y/(1) = 3
Phương trình tiếp tuyến tại điểm M(1 ;1):
y -1 = 3(x -1) 
 y = 3x – 2
c) ( 1đ ) Ta có : 
 Û -x3 + 3x2 – 1 = m – 1 
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số với đường thẳng y = m – 1
Nếu thì phương trình đã cho có 1 nghiệm
Nếu thì phương trình đã cho có 2 nghiệm
Nếu 0 < m <4 thì phương trình đã cho có 3 nghiệm
0.25
0.25
0.5
0.5
0.5
 0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
CÂU 2
( 2đ )
a) ( 1đ) Û 32x + 3.3x – 4 = 0 (1)
Đặt t = 3x ( t > 0)
Û t2 + 3t – 4 = 0 
Với t = 1 Û 3x = 1 x = 0
b) ( 1đ ) ( 2)
Điều kiện: 
( 2 )
log3 [(x + 2)(x – 2)] log35 Û (x +2)(x – 2) 5 
 Û x2 – 9 0 
Kết hợp với điều kiện bất phương trình đã cho có nghiệm 2
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
CÂU 3
( 1đ )
 ( 1đ ) Ta có: 	
 Û 4x3 – 4x = 0 
f(0) = -3
f(1) = -4
f(2) = 5
Vậy 
0.25
0.25
0.25
0.25
CÂU 4
( 3đ )
C
M
450
6
S
B
A
O
a) ( 0,75đ ) Thiết diện qua trục là DSAB vuông cân tại S nên = = 450
 Tính: OA = (DSOA vuông tại O)
Sxq = rl = .OA.SA = ..6 = (cm2)
Stp = Sxq + Sđáy = + = (cm2)
b) ( 0,75đ )Tính: SO = (DSOA vuông tại O)
 V = = = (cm3)
 c) ( 1.25đ ) Gọi M là trung điểm của AC .
Thiết diện (SAC) qua trục tạo với đáy 1 góc 600: = 600
Tính: SM = (DSMO vuông tại O)
 Tính: OM = (DSMO vuông tại O)
Tính: AM = = (DMOA vuông tại M)
 Þ AC = 2AM = 
 SSAC = SM.AC = .. = (cm2)
0.25
 0.25
0.25
0.25
 0.25
0.5
 0.25
0.25
0.25
0.25
0.25