Công thức Toán ôn thi Đại học và Tốt nghiệp
HÀM SỐ MŨLOGARIT
I. Hàm số mũ
• y=ax; TXĐ D=R
• Bảng biến thiên
Bạn đang xem tài liệu "Công thức Toán ôn thi Đại học và Tốt nghiệp", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
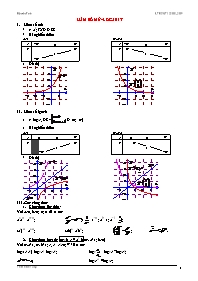
HÀM SỐ MŨ-LOGARIT
Hàm số mũ
y=ax; TXĐ D=R
Bảng biến thiên
a>1 0<a<1
x
-¥ 0 +¥
x
-¥ 0 +¥
y
+¥
1
-¥
y
+¥
1
-¥
Đồ thị
Hàm số lgarit
y=logax, ĐK:; D=(0;+¥)
Bảng biến thiên
a>1 0<a<1
x
0 0 +¥
x
0 0 +¥
y
+¥
1
-¥
y
+¥
1
-¥
Đồ thị
Các công thức
Công thức lũy thừa:
Với a>0, b>0; m, nÎR ta có:
anam =an+m; ;(=a-m ; a0=1; a-1=);
(an)m =anm ; (ab)n=anbn; ; .
Công thức logarit: logab=cÛac=b (00)
Với 00; aÎR ta có:
loga(x1x2)=logax1+logax2 ; loga= logax1-logax2;
; logaxa=alogax;
;(logaax=x); logax=;(logab=)
logba.logax=logbx; alogbx=xlogba.
Phương trình và bất phương trình mũ-logarit
Phương trình mũ-logarit
Phương trình mũ:
4Đưa về cùng cơ số
+0<a¹1: af(x)=ag(x) (1) Û f(x)=g(x).
+ 0<a¹1: af(x)=b Û.
Chú ý: Nếu a chứa biến thì (1) Û(a-1)[f(x)-g(x)]=0
4Đặt ẩn phụ: Ta có thể đặt t=ax (t>0), để đưa về một phương trình đại số..
Lưu ý những cặp số nghịch đảo như: (2), (7), Nếu trong một phương trình có chứa {a2x;b2x;axbx} ta có thể chia hai vế cho b2x(hoặc a2x) rồi đặt t=(a/b)x (hoặc t=(b/a)x.
4Phương pháp logarit hóa: af(x)=bg(x)Û f(x).logca=g(x).logcb,với a,b>0; 0<c¹1.
Phương trình logarit:
4Đưa về cùng cơ số:
+logaf(x)=g(x)Û +logaf(x)= logag(x)Û.
4Đặt ẩn phụ.
Bất phương trình mũ-logarit
Bất phương trình mũ:
4 af(x)>ag(x) Û; 4 af(x)³ag(x) Û.
Đặt biệt:
* Nếu a>1 thì: af(x)>ag(x) Û f(x)>g(x);
af(x)³ag(x) Û f(x)³g(x).
* Nếu 0ag(x) Û f(x)<g(x);
af(x)³ag(x) Û f(x)£g(x).
Bất phương trình logarit:
4logaf(x)>logag(x)Û; 4logaf(x)³logag(x)Û .
Đặt biệt:
+ Nếu a>1 thì: logaf(x)>logag(x) Û ;
+ Nếu 0logag(x) Û .
*
* *
ĐẠO HÀM
Quy tắc tính đạo hàm
Công thức tính đạo hàm
ĐỌC THÊM: }; ¾
Ý nghĩa hình học của đạo hàm
Dạng toán: Cho hàm số y=f(x) có đồ thị (C). Viết phương trình tiếp tuyến với (C) tại điểm M(x0;y0). Khi đó phương trình tiếp tuyến của đường cong (C): (*).
Đạo hàm cấp cao
Đạo hàm cấp 2: y’’=(y’)’
Đạo hàm cấp 3: y’’’=(y’’)’
Đạo hàm cấp 4: y(4)=(y’’’)’
..
Đạo hàm cấp n: y(n)=(y(n-1))’.
*
* *
ỨNG DỤNG CỦA ĐẠO HÀM
Các dạng toán thường gặp về ứng dụng của đạo hàm:
Hàm số đồng biến, nghịch biến trên khoảng (a;b):
Y f(x) đồng biến Û f'(x)³ 0 Y f(x) nghịch biến Û f'(x)£ 0
x a b x a b
y' + y' -
y y
(xem lại các bài toán xét dấu nhị thức bậc nhất, tam thức bậc hai trong chương trình lớp 10)
Quy tắc tìm CĐ, CT:
Quy tắc I: 1) Tìm f'(x)
2) Tìm các điểm tới hạn (điểm làm cho đạo hàm bằng 0 hoặc không xác định)
3) Xét dấu đạo hàm
4) Từ bảng biến thiên suy ra cực trị.
x a x0 b x a x0 b
y' + 0 - y' - 0 +
y CĐ y CT
Quy tắc II: 1) Tính f'(x), giải phương trình f'(x)=0 tìm các nghiệm xi (i=1;2;)
2) Tính f''(xi)
3) f''(xi)>0Þ xi là điểm CT; f''(xi)<0Þ xi là điểm CĐ.
((x0 là nghiệm của phương trình y’’=0)
Tính lồi, lõm, điểm uốn:
x a x0 b
y'' - 0 +
(C) lồi Điểm uốn lõm
U(x0;y0)
Tìm giá trị lớn nhất (GTLN), giá trị nhỏ nhất (GTNN)
Tìm GTLN,GTNN trên một khoảng: lập bảng biến thiên trên khoảng (a;b) rồi dựa vào đó để kết luận. Nếu trên khoảng (a; b) hàm số đơn trị thì GTLN hoặc GTNN trùng với giá trị cực trị của hàm số.
Tìm GTLN,GTNN trên một đoạn [a; b]:
1) Tìm các điểm tới hạn x1, x2, , xn của f(x) trên đoạn [a;b]
2) Tính f(a), f(x1), f(x2), ,f(xn), f(b)
3) Tìm số lớn nhất M và số nhỏ nhất m trong các số trên
.
*
* *
TIỆM CẬN
Định nghĩa:
(d) là tiệm cận của (C)
Cách xác định tiệm cận
Tiệm cận đứng: .
Tiệm cận ngang: .
Tiệm cận xiên: TCX có phương trình: y=lx+m trong đó:
.
Các trường hợp đặc biệt:
*Hàm số bậc nhất trên bậc nhất (hàm nhất biến)
+TXĐ: D= R\
+TCĐ:
+TCN:
* Hàm số bậc hai trên bậc nhất (hàm hữu tỷ)
+TXĐ: D= R\
+TCĐ:
+TCX: Þ TCX: y=lx+m
KHẢO SÁT VÀ MỘT SỐ BÀI TOÁN LIÊN QUA N ĐẾN KHẢO SÁT HÀM SỐ
KHẢO SÁT HÀM SỐ
Tìm tập xác định D.
Xét sự biến thiên:
Tính y’.
Giải phương trình: y’=0 Þ nghiệm xi thay vào hàm sốÞyi (i=1,2,3).
Tính giới hạn.
2a) Đối với hàm phân thức: tìm tiệm cận
2b) Đối với hàm đa thức: Xét tính lồi lõm, điểm uốn.
Tính y’’.
Giải phương trình: y’’=0 Þ nghiệm xi thay vào hàm sốÞyi (i=1,2,3).
Lập bảng xét dấu y’’_kết luận lồi, lõm, điểm uốn.
Lập bảng biến thiên_kết luận CĐ, CT, chiều biến thiên.
Vẽ đồ thị:
Cho điểm đặc biệt.
Biểu diễn theo thứ tự: tiệm cận (nếu có); các điểm cực trị; điểm uốn; điểm đặc biệt lên hệ trục tọa độ.
ĐỌC THÊM:
}Bảng tóm tắt khảo sát bốn hàm số cơ bản
Hàm đa thức bậc ba y=ax3+bx2+cx+d (a¹0)
1/ TXĐ: D=.
2/ Đạo hàm y'=3ax2+2bx+c; y''=6ax+2b.
Đồ thị luôn có một tâm đối xứng trùng với điểm uốn U.
y’=0 có hai nghiệm phân biệt
y’=0 có nghiệm kép
y’=0 vô nghiệm
a>0
a<0
Hàm đa thức (hàm trùng phương) y=ax4+bx2+c (a¹0)
1/ TXĐ: D=.
2/ Đạo hàm y'=4ax3+2bx=2x(2ax2+b); y''=12ax2+2b. Đồ thị nhận trục tung làm trục đối xứng.
y’=0 có ba nghiệm
y’=0 có một nghiệm
a>0
a<0
Hàm số bậc nhất trên bậc nhất (hàm nhất biến) :
+TXĐ: D=\;
+TCĐ: +TCN:
D>0
D<0
Hàm số bậc hai trên bậc nhất (hàm hữu tỷ) :
+TXĐ: D=\
+TCĐ: +TCX: Þ TCX: y=lx+m
am>0
y'=0 có hai nghiệm phân biệt
Các giới hạn:
y'=0 vô nghiệm
Các giới hạn:
am'<0
y'=0 có hai nghiệm phân biệt
Các giới hạn:
y'=0 vô nghiệm
Các giới hạn:
Các bảng xét dấu thường gặp:
¾
MỘT SỐ BÀI TOÁN LIÊN QUA N ĐẾN KHẢO SÁT HÀM SỐ
TIẾP TUYẾN CỦA ĐỒ THỊ
Cho hàm số y=f(x) có đồ thị (C).
f’(x0)_hệ số góc của tiếp tuyến với (C) tại điểm có hoành độ x0.
Phương trình tiếp tuyến của (C) tại điểm M(x0;y0)Î(C) là:
y-y0=f’(x0)(x-x0)
Điều kiện để đường thẳng y=kx+b tiếp xúc với (C):
MỘT SỐ DẠNG TOÁN THƯỜNG GẶP:
Lập phương trình tiếp tuyến của (C) tại điểm M(x0;y0)Î(C).
Lập phương trình tiếp tuyến của (C) khi biết hệ số góc k.
Lập phương trình tiếp tuyến của (C) biết tiếp tuyến đi qua điểm A(xA;yA):
+Viết phương trình đường thẳng (d) qua A có hệ số góc k: y=k(x-xA)+yA (d).
+Giải phương trình Þk rồi thay vào (d) ta được phương trình tiếp tuyến.
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐỒ THỊ
Cho hai hàm số y=f(x) có đồ thị (C1) và y=g(x) có đồ thị (C2). Khảo sát sự tương giao giữa hai đồ thị (C1) và (C2) tương đơưng với khảo sát số nghiệm của phương trình: f(x) =g(x) (1). Số giao điểm của (C1) và (C2) đúng bằng số nghiệm của phương trình hoành độ giao điểm (1).
(1) vô nghiệm Û (C1) và (C2) không có điểm chung.
(1) có n nghiệm Û (C1) và (C2) có n điểm chung.
(1) có nghiệm đơn x1 Û (C1) và (C2) cắt nhau tại N(x1;y1).
(1) có nghiệm kép x0 Û (C1) tiếp xúc (C2) tại M(x0;y0).
*
* *
TÍCH PHÂN-ỨNG DỤNG
Bảng nguyên hàm
Nguyên hàm của những hàm số sơ cấp thường gặp
Nguyên hàm của những hàm số thường gặp
Nguyên hàm của những hàm số hợp
TÍCH PHÂN
TÍNH CHẤT
a. Công thức:; trong đó F(x) là một nguyên hàm của f(x).
b.Tính chất:
·
·
· f(x)³0 trên đoạn [a;b]Þ
f(x)³g(x) trên đoạn [a;b]Þ
m£f(x)£M trên đoạn [a;b]Þ m(b-a)££M(b-a)
t biến thiên trên đoạn [a;b]ÞG(t)= là một nguyên hàm của f(t) và G(a)=0.
Các phương pháp tính
i. Phương pháp đổi biến số
Đổi biến loại 1
*ĐẶt x=u(t)Þdx=u’(t)dt
*Đổi cận: a=u(a),b=u(b)
Khi đó: .
ÆChú ý: Phương pháp đổi biến loại 1 thường áp dụng cho các tích phân có dạng sau:
:đặt x=asint (hoặc x=acost); (nÎN).
: đặt x=a/sint (hoặc x=a/cost).
: đặt x=atant (hoặc x=acott).
Đổi biến loại 2
*ĐẶt t=v(x)Þdt=v’(x)dx
*Đổi cận: x=aÞt=v(a), x=bÞt=v(b)
ii. Phương pháp tích phân từng phần
ÆChú ý: Nếu tích chứa tích của p(x) với hàm logarit trong đó p(x)¹1/x ta đặt u=logarit, dv=p(x)dx; các dạng khác đặt ngược lại.
Tích phân hàm phân thức
Nếu def p(x)>defq(x) thì chia đa thức trước khi lấy tích phân.
Các dạng khác thông thường ta dùng phương pháp đổi biến số hoặc phân tích thành tích các phân thức tối giản.
ÆChú ý:
Ứng dụng tích phân
Diện tích
x
y
O
f(x)
g(x)
b
a
Cho hai hàm số y=f(x) và y=g(x) có đồ thị (C1), (C2). Diện tích hình phẳng giới hạn bởi (C1), (C2) và hai đường thẳng x=a, x=b được tính bởi công thức:
ÆChú ý:
Nếu diện tích thiếu các đường thẳng x=a, x=b
ta phải giải phương trình f(x)=g(x) để tìm a, b.
x
y
O
f(x)
x(x)
b
a
y
x
c
d
O
Thể tích
Thể tích do hình phẳng giới hạn bởi
{(C):y=f(x),y=0,x=a,x=b} quay quanh Ox
được tính bởi công thức:
Thể tích do hình phẳng giới hạn bởi
{(C): x=x(y), x=0, y=c, y=d} quay quanh Oy
được tính bởi công thức:
Thể tích tròn xoay do hình phẳng giới hạn bởi hai đường y=f(x),y=g(x) quay quanh Ox (f(x)³g(x), "xÎ[a;b]) đơực tính bởi công thức:.
*
* *
SỐ PHỨC
(z=a+bi; i2=-1)
Định nghĩa
Trong toán học, trường số phức, ký hiệu là C. Có nhiều phương pháp xây dựng trường số phức một cách chặt chẽ bằng phương pháp tiên đề.
Gọi R là trường số thực. Ký hiệu C là tập hợp các cặp (a; b) với a, bÎR.
Trong C, định nghĩa hai phép toán cộng và nhân như sau:
(a;b)+(c;d)=(a+c;b+d)
(a;b)*(c;d)=(ac-bd;ad+bc)
thì C là một trường.
Ta có thể lập một đơn ánh từ tập số thực R vào C bằng cách cho mỗi số thực a ứng với cặp (a;0)ÎC. Khi đó 0®(0;0), 1®(1;0), -1®(-1;0)... Nhờ phép nhúng, ta đồng nhất tập các số thực R với tập con các số phức dạng (a,0), khi đó tập các số thực R là tập con của tập các số phức C và C được xem là một mở rộng của R. Kí hiệu i là cặp (0;1)ÎC. Ta có i2=(0;1)*(0;1)=(−1;0)=−1.
Số phức i được gọi là đơn vị ảo, tất cả các số phức dạng bi được gọi là các số ảo (thuần ảo).
Một số khái niệm quan trọng trong trường số phức
Dạng đại số của số phức
Trong trường số phức, tính chất của đơn vị ảo i đặc trưng bởi biểu thức i2=−1 . Mỗi số phức z đều được biểu diễn duy nhất dưới dạng: z=a+bi. trong đó a, b là các số thực. Dạng biểu diễn này được gọi là dạng đại số của số phức z.
Với cách biểu diễn dưới dạng đại số, phép cộng và nhân các số phức được thực hiện như phép cộng và nhân các nhị thức bậc nhất với lưu ý rằng i2 = –1. Như vậy, ta có:
(a+b.i)+(c+d.i)=(a+c)+(b+d).i
(a+b.i)(c+d.i)=(a.c-b.d)+(b.c+a.d).i
Mặt phẳng phức
Trong hệ toạ độ Đề các, có thể dùng trục hoành chỉ tọa độ phần thực còn trục tung cho tọa độ phần ảo để biểu diễn một số thực z=x +yi. Khi đó mặt phẳng tọa độ được gọi là mặt phẳng phức.
Số thực và số thuần ảo
Nếu b=0, số phức có dạng z=a được gọi là số thực, nếu a=0, số phức b.i được gọi là thuần ảo.
Số phức liên hợp
Cho số phức dưới dạng đại số , số phức được gọi là số phức liên hợp của z.
Một số tính chất của số phức liên hợp:
là một số thực.
Phép chia hai số phức dưới dạng đại số: .
Mođun và Argumen
Cho . Khi đó . Căn bậc hai của được gọi là mođun của z, ký hiệu là |z| . Như vậy .
Có thể biểu diễn số phức z = a + bi trên mặt phẳng tọa độ bằng điểm M(a,b), góc j giữa chiều dương của trục Ox và vectơ, được gọi là argumen của số phức z, ký hiệu là arg(z).
Một vài tính chất của môđun và argumen .
arg(z1z2) = arg(z1) + arg(z2), .
Dạng lượng giác của số phức
Định nghĩa
Số phức z=a+bi có thể viết dưới dạng hay, khi đặt , ta có .
Cách biểu diễn này được gọi là dạng lượng giác của số phức z.
Phép toán trên các số phức viết dưới dạng lượng giác
Phép nhân và phép chia các số phức dưới dạng lượng giác.
Cho hai số phức dưới dạng lượng giác ,
Khi đó
Lũy thừa tự nhiên của số phức dưới dạng lượng giác (công thức Moirve).
Khai căn số phức dưới dạng lượng giác.
Mọi số phức z khác 0 đều có đúng n căn bậc n, là các số dạng trong đó , k = 0,1,...n −1.
Ví dụ: Điểm khác biệt quan trong nhất khi mở rộng thành trường số phức từ trường số thực là tính đóng với các phương trình đại số. Mỗi phương trình đại số bậc n đều có đúng n nghiệm. Nói riêng, phương trình xn có n nghiệm, hay là căn bậc n của số phức khác 0 bất kì có n giá trị. Điều này là hoàn chỉnh của mệnh đề trong số thực "mọi số thực dương có 2 căn bậc hai".
Ví dụ:
Æ có hai căn bậc hai là 1 và − 1.
Æ có hai căn bậc hai là i và -i .
Æ có hai căn bậc hai là:
và .
.
Æ có hai căn bậc hai là:
và .
Æ có ba căn bậc ba là:
, và .
Æ có ba căn bậc ba là:
, và .
*
* *
Tài liệu đính kèm:
 Cong thuc Toan 122009.doc
Cong thuc Toan 122009.doc





