Đề kiểm tra học kỳ II môn: Toán - Lớp 11(chương trình chuẩn)

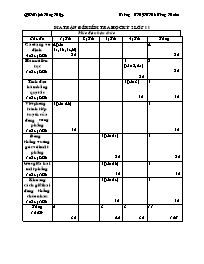
Ma trận đề kiểm tra học kỳ 2 lớp 11
 Mức độ nhận thức
Chủ đề
1(TL)
2(TL)
3(TL)
4(TL)
Tổng
Các dạng vô định
4 câu(20%)
4(câu 1a,1b,1c,1d)
 2đ
4
 2đ
Hàm số liên tục
1 câu(20%)
1
(câu2, 4a)
 2đ
2
 2đ
Tính đạo hàm bằng quy tắc
1 câu(20%)
1(câu 3)
 1đ
1
 1đ
Viết phương trình tiếp tuyến của đường cong phẳng
1 câu(10%)
1(câu 4b)
 1đ
1
 1đ
Đường thẳng vuông góc với mặt phẳng
1 câu(20%)
1(câu 5a)
 2đ
1
 2đ
Góc giữa hai mặt phẳng
1 câu(10%)
1(câu 5b)
 1đ
1
 1đ
Khoảng cách giữi hai đường thẳng chéo nhau
1 câu(10%)
1(câu 5c)
 1đ
1
 1đ
Tổng
100%
5
 3đ
3
 4đ
3
 3đ
11
 10đ
Bảng mô tả:
Câu 1: Nhận dạng được các dạng vô định của giới hạn hàm số và tính được các giới hạn đó
Câu 2: Vận dụng được định nghĩa hàm số liên tục tại một điểm trong việc tìm tham số để hàm số liên tục
Câu 3: Vận dụng được công thức tính đạo hàm cấp cao trong việc tính đạo hàm của hàm số hợp
Câu 4: a, Vận dụng được tính liên tục của làm số trong việc chứng minh phương trình có nghiệm trên khoảng
 b, Nhận dạng được các loại tiếp tuyến(viết PTTT biết hệ số góc
Câu 5: a, Vận dụng được phương pháp để chứng minh đường thẳng vuông góc với mặt phẳng
 b , Vận dụng tính góc giữi hai mặt phẳng
 c , Vận dụng tính khoảng cách giữi hai đường thẳng chéo nhau
Sở gd&đt thanh hoá đề kiểm tra học kỳ ii
 Môn: Toán-Lớp 11(chương trình chuẩn)
 Thời gian làm bài:90 phút
Cõu 1: Xỏc định dạng vụ định và tớnh cỏc giới hạn sau: 
a. ; 	b. 
c. 	d. 
nếu x <2
nếu x³ 2
Câu 2: Tỡm số thực m sao cho hàm số:
liờn tục tại x = 2
Cõu 3:Tớnh biết: . 
Câu 4:Cho đường cong (C) cú phương trỡnh: .
a) Chứng minh rằng phương trỡnh y’=0 cú ớt nhất một nghiệm thuộc khoảng (0;2)
b) Viết phương trỡnh tiếp tuyến của đường cong (C). Biết rằng hệ số gúc của tiếp tuyến bằng 5.
Câu 5:
Cho hỡnh chúp S.ABCD cú , đỏy ABCD là hỡnh thang vuụng tại A và D với , . Gọi I là trung điểm của AB.
a) Chứng minh rằng: ;
b) Tớnh gúc tạo bởi giữa hai mặt phẳng (ABCD) và (SCD);
c) Tớnh khoảng cỏc giữa hai đường thẳng chộo nhau AB và SC.
-----------------------------------------------
đáp án
Điểm
*Đại số:
Cõu 1: a. 
 b. 
	= 
c. 
d. 	
=
Câu 2: Ta cú: 
Từ đú: 
Với m = thỡ f(x) liờn tục tại x = 2. 
Câu 3: 
0,5đ
0,5đ
0,5đ
0,5đ
1đ
1đ
Cõu 4: 
a) Xột hàm số f(x) = x3 + 2x – 5
Ta cú: f(0) = -5 và f(2) = 7. 
Do đú f(0).f(2) < 0.
(Cỏch 2: f(1).f(2) = -14 < 0)
y = f(x) là một hàm số đa thức nờn liờn tục trờn R. Do đú nú liờn tục trờn đoạn [0;2]. 
Suy ra phương trỡnh f(x) = 0 cú ớt nhất một nghiệm x0 .
b)Do phương trỡnh tiếp tuyến với đường cong (C) cú hệ số gúc k = 5, nờn ta cú:
 f’(x0) = 5 (với x0 là hoành độ tiếp điểm)
 3 + 2 = 5 = 1 
*Khi x0 = 1 y0 = -2, ta cú phương trỡnh tiếp tuyến là: 
y + 2 = 5(x – 1)
 y = 5x -7
*Khi x0 = -1 y0 = -8, ta cú phương trỡnh tiếp tuyến là: 
y + 8 = 5(x + 1)
 y = 5x -3
Vậy cú hai phương trỡnh tiếp tuyến với đường cong (C) cú hệ số gúc bằng 5 là:
y = 5x -7 và y = 5x -3
1đ
1đ
Câu 5:Lưu ý: Học sinh vẽ đúng hình được 0,5 đ
a)Chứng minh :
ABCD là hỡnh thang vuụng tại A và D và I là trung điểm của AB, nờn tứ giỏc AICD là hỡnh vuụng.
Theo đề ra, ta cú: 
 Hay 
Từ (1) và (2) ta cú: (đpcm)
b) Tớnh gúc tạo bởi giữa hai mặt phẳng (ABCD) và (SCD):
Ta cú: 
gúc tạo bởi giữa hai mặt phẳng (ABCD) và (SCD) là gúc: 
Xột tam giỏc SAD vuụng tại A, ta cú:
Vậy gúc giữa hai mặt phẳng (ABCD) và (SCD) bằng 600.
c)Tớnh khoảng cỏc giữa hai đường thẳng chộo nhau AB và SC:
Mặt khỏc, ta cú: nờn khoảng cỏch giữa hai đường thẳng AB và SC chớnh bằng khoảng cỏch từ một điểm bất kỳ nằm trờn đường thẳng AB đến mặt phẳng (SCD).
Trong tam giỏc vuụng SAD vuụng tại A, gọi H là hỡnh chiếu vuụng gúc của A lờn cạnh SD, khi đú ta cú: 
Áp dụng hệ thức lượng vào tam giỏc vuụng SAD vuụng tại A ta cú:
(*)
Ta cú: SD2 = SA2 + AD2 
 (3)
Thay (3) vào (*) ta được:
Vậy khoảng cỏch giữa hai đường thẳng chộo nhau AB và SC bằng .
2đ
1đ
1đ