Đề kiểm tra học kỳ I môn Toán - Lớp 10 chương trình nâng cao

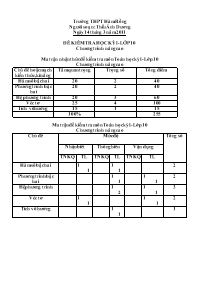
Trường THPT Hàm Rồng
Người soạn:Thiều Ánh Dương
Ngày 14 tháng 3 năm 2011
ĐỀ KIỂM TRA HỌC KỲ I-LỚP 10
Chương trình nâng cao
Ma trận nhận thức đề kiểm tra môn Toán học kỳ I-Lớp 10
Chương trình nâng cao
Chủ đề hoặc mạch kiến thức,kĩ năng
Tầm quan trọng
Trọng số
Tổng điểm
Hàm số bậc hai
20
2
40
Phương trình bậc hai
20
2
40
Hệ phương trình
20
 3
60
Véc tơ
25
4
100
Tích vô hướng
15
1
15
100%
255
Ma trận đề kiểm tra môn Toán học kỳ I-Lớp 10
Chương trình nâng cao
Chủ đề
Mức độ
Tổng số
 Nhận biết
Thông hiểu
Vận dụng
TNKQ
TL
TNKQ
TL
TNKQ
TL
Hàm số bậc hai
1 
 1
1 
 1 
2
Phương trình bậc hai
1 
 1 
1
 1
2
Hệ phương trình
1
 2 
1
 1
3
Véc tơ
1 
 1
1 
 1
2
Tích vô hướng
1
 1
1
 ĐỀ KIỂM TRA HỌC KỲ I
Môn: Toán- Lớp 10
Thời gian làm bài: 90 phút
ĐỀ A
Câu I: (2 điểm)
 Cho hàm số bậc hai: y= ax2 -2x - 3
 1: Tìm a biết rằng đồ thị hàm số đi qua A(2;-3)
 2: Tìm m để phương trình sau có 4 nghiệm phân biệt
Câu II: (2 điểm)
 Giải hệ phương trình
Câu III: (2 điểm)
 Cho phương trình: x2 + 2(m+1)x + m - 2 =0
 1: Tìm m để phương trình có hai nghiệm âm phân biệt
 2: Giả sử x1; x2 là hai nghiệm của phương trình. Tìm m sao cho x1 - 2x2 = - 6
Câu IV: (3 điểm)
 Cho tam giác đều ABC cạnh a, trọng tâm G
 1: Tính các tích vô hướng: và 
 2: Tìm điểm I sao cho: 
 3: Tìm tập hợp điểm M sao cho:
Câu V: (1 điểm)
 Tùy theo a tìm giá trị nhỏ nhất của biểu thức
....................................................................................................................
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KỲ I
Môn: Toán- Lớp 10
Thời gian làm bài: 90 phút
ĐỀ A
Câu-ý
Nội dung
Điểm
I/1
+ (P) đi qua A(2;-3) nên
 4a-7=-3
+Giải hệ a=1 Vậy (P) y=x2-2x-3
 0,5
0,5
I/2
+PT: 
Vẽ đồ thị hàm số y= 
+Phương trình có 4 nghiệm phân biệt khi và chỉ khi đường thẳng y=m-3 (Cùng phương ox) cắt ĐT hàm số tại 4 điểm.Căn cứ ĐT -1<m<0
0,5
 0,5
II
Hệ PT 
1,0
1,0
III/1
+Phương trình có hai nghiệm âm phân biệt khi và chỉ khi
+Giải tìm được m>2
0,5
 0,5
III/2
+. PT có hai nghiệm x=-m-1
+Nếu thay vào điều kiện 
Ta được: 
+Nếu thay vào điều kiện ta được: hệ VN
0,5
0,25
0,25
IV/1
 + 
 + + 
0,5
0,5
IV/2
Vậy Hay I là đỉnh thứ tư của hình bình hành GBCI
0,5
0,5
IV/3
Vậy MG=MI .Tập hợp điểm M là đường thẳng trung trực của GI
0,5
0,5
V
Xét hệ PT 
D=2a2 -a ; Dx=7a ; Dy=-3a
a) Nếu 
Dấu bằng xảy ra khi x=7/(2a-1);y=-3/(2a-1)
Vậy Minf=0 khi x=7/(2a-1);y=-3/(2a-1)
b) Nếu a=0
f=(2x+4y+2)2 +(x+2y+1)2=5(x+2y+1)2 0
Vậy Minf=0 khi x+2y+1=0 
c) Nếu a=1/2
 =
Vậy minf=1/2 khi 
0,25
0,25
0,25
0,25