Đề kiểm tra chương I - Giải tích lớp 12

ĐỀ KIỂM TRA CHƯƠNG I-GIẢI TÍCH 12
********************
I.Mục đích, yêu cầu:
 +Kiểm tra kiến thức và kĩ năng chương I, lấy điểm một tiết.
II.Mục tiêu:
 +Khắc sâu các khái niệm, các định lý về tính đơn điệu, cực trị, giá trị lớn nhất, giá trị nhỏ nhất của hàm số, các tiệm cận của đồ thị hàm số.
+Rèn luyện kĩ năng tìm các khoảng đồng biến, nghịch biến, cực trị, GTLN và GTNN của hàm số và các tiệm cận của đồ thị hàm số.
+Khảo sát sự biến thiên và vẽ đồ thị hàm số.
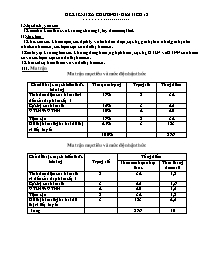
 III . Ma trận	
Ma trận mục tiêu và mức độ nhận thức
Chñ ®Ò hoÆc m¹ch kiÕn thøc kÜ n¨ng
TÇm quan träng
Träng sè
Tæng ®iÓm
TÝnh ®¬n ®iÖu cña hµm sè vµ dÊu cña ®aä hµm cÊp 1
17%
2
34
Cùc trÞ cña hµm sè
15%
3
45
GTLN & GTNN
10%
4
40
TiÖm cËn
17%
2
34
§å thÞ hµm sè giao hai ®å thÞ vµ tiÕp tuyÕn
41%
3
123
100%
276
Ma trận mục tiêu và mức độ nhận thức
Chñ ®Ò hoÆc m¹ch kiÕn thøc kÜ n¨ng
Träng sè
Tæng ®iÓm
Theo ma trận nhận thức
Theo thang điểm 10
TÝnh ®¬n ®iÖu cña hµm sè vµ dÊu cña ®aä hµm cÊp 1
2
34
1,2
Cùc trÞ cña hµm sè
3
45
1,6
GTLN & GTNN
4
40
1,5
TiÖm cËn
2
34
1,2
§å thÞ hµm sè giao hai ®å thÞ vµ tiÕp tuyÕn
3
123
4,5
 Tổng 
276
10
III.Ma trận đề:
Chủ đề hoặc mạnh kiến thức , kĩ năng
Mức độ nhận thức – Hình thức câu hỏi 
Tổng
(1)
(2)
(3)
`(4)
TN
TL
TN
TL
TN
TL
TN
TL
Sự đồng biến, nghịch biến của hàm số
Câu 1,2
0.8
Câu 8
0.4
3
1.2
Cực trị của hàm số
Câu 3,4,5
1.2
Câu 9
0.4
4
1.6
GTLN và GTNN củahàm số 
Câu 12
1.5
1
1.5
Đường tiệm cận
Câu 6,7
0.8
Câu 10
0.4
3
1.2
Khảo sát sự biến thiên và vẽ đồ thị hàm số
Câu
11a
3
Câu
11b
1.5
2
4.5
Tổng
7
2,8
4
4.2
2
3
13
10
BẢNG MÔ TẢ NỘI DUNG
CÂU 1 : Nhân biết các bước xét tính đơn điệu của hàm số.
CÂU 2: Nhận biết các khoảng đồng biến nghịch biến.
CÂU 3: Nhận biết các khoảng đồng biến nghịch biến
CÂU 4: Nhận biết điểm cực trị của hàm số.
CÂU 5: Nhận biết điểm cực trị của hàm số.
CÂU 6: Nhận biết điểm cực trị của hàm số.
CÂU 7: Nhận biết điều kiện để hàm số có cực trị .
CÂU 8: Nhận biết được tiệm cận của hàm số.
CÂU 9: Nhận biết được tiệm cận của hàm số.
CÂU 10: Nhận biết được số tiệm cận của hàm số.
CÂU 11: 
Biết khảo sát và vẽ đồ thị hàm số
Biết xác định số giao điểm của hai đồ thị.
CÂU 12: Biết GTLN & GTNN của hàm số trên một đoạn.
IV.Đề:
A.Trắc nghiệm(4đ) Học sinh chọn ý đúng trong mổi câu.
Câu 1:Cho hàm số,một học sinh thực hiện các bước giải để tìm các khoảng đồng biến, 
 nghịch biến như sau:
B1:TXĐ:D=R
B2:;y’=0x=1
B3: BBT 
x
- -1 1 + 
y’
 - 0 + 0 -
y
B4:Vậy hàm số đồng biến trên các khoảng (-;-1); (1;+) và nghịch biến trên khoảng (-1;1)
Học sinh giải bài toán trên:
 A. Giải đúng hoàn toàn. B.Sai từ bước 1 C.Sai từ bước 2. D.Sai từ bước 3.
Câu 2: Cho hàm số y=-x3+3x2-3x+1. Tìm mệnh đề đúng?
A. Hàm số đồng biến trên R.
B. Hàm số nghịch biến trên R.
C. Hàm số đồng biến trên khoảng (-;1) và nghịch biến trên khoảng (1;+).
D. Hàm số nghịch biến trên khoảng (-;1) và đồng biến trên khoảng (1;+).
Câu 3: Hàm số y= nghịch biến trên:
 	A. R B. (-;2) C.(-3;+) D.(-2;+).
Câu 4: Số điểm cực trị của hàm số y=x4-2x2+1 là:
A. 1 B. 3 C. 2 D.4
Câu 5: Điểm cực tiểu của hàm số y=2x3-3x2-2 là:
A. x=0 B. x=-1 C. x=1 D. x=2
Câu 6: Hàm số y=sin2x đạt cực trị tại điểm:
A .x= B. x= C. x= D. x=k
Câu 7: Hàm số y= đạt cực đại và cực tiểu khi:
A. m0 D. m>2
Câu 8: Đồ thị hàm số y= có các đường tiệm cận là:
A.x=1 và y=-1 B.x=1 và y=1 C.x=-1 và y=1 D.x=-1 và y=-1
Câu 9: Cho hàm số y=.Tìm mệnh đề đúng?
A. Đồ thị hàm số không có tiệm cận ngang.
B. Đồ thị hàm số có các tiệm cận đứng x=1 và x=-1.
C. Đồ thị hàm số có tiệm cận ngang y=1.
D. Đồ thị hàm số không có các tiệm cận đứng .
Câu 10: Số các đường tiệm cận của đồ thị hàm số y= là:
A. 1 B. 2 C. 3 D. 4
B.Tự luận: (6đ)
Câu 11Cho hàm số y=x3-3x2+2
1.Khảo sát sự biến thiên và vẽ đồ thị hàm số.
2.Tìm giá trị của m để phương trình :
 -x3+3x2+m=0 có 3 nghiệm thực phân biệt.
Câu 12 Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y=x+
V.Đáp án và biểu điểm:
A/ Trắc nghiệm:
1
2
3
4
5
6
7
8
9
10
D
B
D
B
C
A
A
C
D
C
Câu
Hướng dẫn chấm
Biểu điểm
11a
.(3đ) Khảo sát sự biến thiên và 
 vẽ đồ thị của hàm số: y=x3-3x2+2(C) 
+ + 
+TXĐ: D=R
0.25
+; 
+y’=3x2-6x
 y’=0
Hàm số đồng biến trên các khoảng 
(-;0), (2;+) và nghịch biến trên khoảng (0;2)
+Hàm số đạt cực đại tại x=0, yCĐ=2
 Hàm số đạt cực tiểu tại x=2, yCT=-2
0.25
0.25
0.25
0.75
0.25
BBT: 
x
- 0 2 + 
y’
 + 0 - 0 +
y
	 2	+	+
-	 -2
0.25
0.75
Câu 11 b
2. (1,5đ)
-x3+3x2+m=0 
x3-3x2+2=m+2\
0,5
Đây là phương trình hoành độ giao điểm của (C) và đường thẳng d: y=m+2
Số nghiệm của phương trình đã cho bằng số giao điểm của (C) và d.
0,5
Do đó phương trình đã cho có 3 nghiệm thực phân biệt (C) và d có 3 giao điểm
 -2<m+2<2
 -4<m<0
0,5
Vậy: -4<m<0
Câu 12 
 (1.5đ) 
 y=x+
+TXĐ: D=[-1;1]
+y’=1-=
+y’=ox=
+y(1)=1
 y(-1)=-1
 y()=
+Vậy Maxy=y()=
 Miny=y(-1)=-1
0.25
0.25
0.25
0.5
0.25