Đề kiểm tra 1 tiết môn Giải tích lớp 12 chương trình nâng cao
ĐỀ KIỂM TRA 1 TIẾT MÔN GIẢI TÍCH LỚP 12
CHƯƠNG TRÌNH NÂNG CAO
Thời gian làm bài :45 phút.
Bài 1:(6.5 điểm )
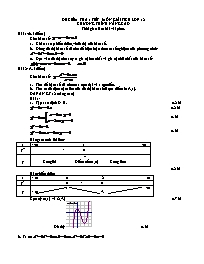
Cho hàm số: y=x3-3x2+1
a. Khảo sát sự biến thiên,vẽ đồ thị của hàm số.
b. Dùng đồ thị hàm số đã cho để biện luận theo m số nghiệm của phương trình:
Bạn đang xem tài liệu "Đề kiểm tra 1 tiết môn Giải tích lớp 12 chương trình nâng cao", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
ĐỀ KIỂM TRA 1 TIẾT MÔN GIẢI TÍCH LỚP 12 CHƯƠNG TRÌNH NÂNG CAO Thời gian làm bài :45 phút. Bài 1:(6.5 điểm ) Cho hàm số: Khảo sát sự biến thiên,vẽ đồ thị của hàm số. Dùng đồ thị hàm số đã cho để biện luận theo m số nghiệm của phương trình: Dựa vào đồ thị trên suy ra giá trị lớn nhất và giá trị nhỏ nhất của hàm số: . Bài 2: (3.5 điểm) Cho hàm số : Tìm để hàm số đã cho có 1 cực đại và 1 cực tiểu. Tìm m để tiệm cận xiên của đồ thị hàm số đi qua điểm M(3,1). ĐÁP ÁN GT 12 (nâng cao) Bài 1: Tập xác định D=R. 0.25đ 0.25đ 0.5đ 0.5đ Bảng xét tính lồi lõm: x - 1 + y’’ - 0 + y /\ Cung lồi Điểm uốn(1,0) Cung lõm 0.25đ Bảng biến thiên x - 0 2 + y’ + 0 - 0 + y 1 + - -3 Cực trị: (0,1) và (2,-3) 0.75đ Đồ thị: 0.5đ b. Ta có Số nghiệm của phương trình là số giao điểm của đồ thị và đường thẳng 0.5đ Phương trình có 1 nghiệm 0.5đ Phương trình có 2 nghiệm(1 đơn,1 kép) 0.5đ Phương trình có 3 nghiệm 0.5đ c. Đặt 0.25đ Ta được hàm số hay 0.25đ Do vậy 0.25đ Dựa vào đồ thị ta có 0.5đ Do đó ta có 0.25đ Bài 2: 0.5đ ; 0. 5đ có 2 nghiệm khi 0.5đ Do vậy hàm số có 1 cực đại và 1 cực tiểu khi y’ đổi dấu 2 lần hay y’=0 có 2 nghiệm phân biệt 0.5đ Tức là y’ có . Vậy hàm số có 1 cực đại và 1 cực tiểu khi 0.5đ Hàm số đã cho viết được về dạng mà Nên đồ thị có tiệm cận xiên là 0.5đ Để đường thẳng này đi qua điểm (3,1) ta có 0.5đ
Tài liệu đính kèm:
 De kiem tra Ds12 Chuong 2co dap an dung lien.doc
De kiem tra Ds12 Chuong 2co dap an dung lien.doc





