Đề cương ôn tập môn Toán Lớp 12 - Phần 3: Ứng dụng của tích phân
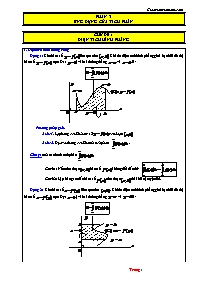
Dạng 1: Cho hàm số liên tục trên . Khi đó diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục Ox ( ) và hai đường thẳng và là:
Phương pháp giải:
Bước 1. Lập bảng xét dấu hàm số trên đoạn .
Bước 2. Dựa vào bảng xét dấu tính tích phân : .
Dạng 2: Cho hàm số liên tục trên . Khi đó diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục Oy ( ) và hai đường thẳng và là:
Bạn đang xem 20 trang mẫu của tài liệu "Đề cương ôn tập môn Toán Lớp 12 - Phần 3: Ứng dụng của tích phân", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
PHẦN 3 ỨNG DỤNG CỦA TÍCH PHÂN CHỦ ĐỀ 1 DIỆN TÍCH HÌNH PHẲNG 1. Diện tích hình thang cong Dạng 1: Cho hàm số liên tục trên . Khi đó diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục Ox () và hai đường thẳng và là: Phương pháp giải: Bước 1. Lập bảng xét dấu hàm số trên đoạn . Bước 2. Dựa vào bảng xét dấu tính tích phân : . Chú ý: có 2 cách tính tích phân + Cách 1: Nếu trên đoạn hàm số không đổi dấu thì: + Cách 2: Lập bảng xét dấu hàm số trên đoạn rồi khử trị tuyệt đối. Dạng 2: Cho hàm số liên tục trên . Khi đó diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục Oy () và hai đường thẳng và là: 2. Diện tích hình phẳng Dạng 1: Cho 2 hàm số và liên tục trên . Khi đó diện tích của hình phẳng (H) giới hạn bởi đồ thị hai hàm số và và hai đường thẳng và là: Phương pháp giải: Bước 1. Lập bảng xét dấu hàm số trên đoạn . Bước 2. Dựa vào bảng xét dấu tính tích phân . Dạng 2: Cho hai hàm số và liên tục trên . Diện tích hình phẳng giới hạn bởi các đường và là: . Trong đó là nghiệm nhỏ nhất và lớn nhất của phương trình Phương pháp giải: Bước 1. Giải phương trình . Giả sử ta tìm được là nghiệm nhỏ nhất và lớn nhất của phương trình . Bước 2. Lập bảng xét dấu hàm số : trên đoạn . Bước 3. Dựa vào bảng xét dấu tính tích phân: . Dạng 3: Cho hai hàm số và liên tục trên . Khi đó diện tích của hình phẳng (H) giới hạn bởi đồ thị hai hàm số và và hai đường thẳng và là: Phương pháp giải: Bước 1. Lập bảng xét dấu hàm số trên đoạn . Bước 2. Dựa vào bảng xét dấu tính tích phân . Dạng 4: Cho hai hàm số và liên tục trên . Diện tích hình phẳng giới hạn bởi các đường và là: . Trong đó là nghiệm nhỏ nhất và lớn nhất của phương trình Phương pháp giải: Bước 1. Giải phương trình . Giả sử ta tìm được là nghiệm nhỏ nhất và lớn nhất của phương trình . Bước 2. Lập bảng xét dấu hàm số : trên đoạn . Bước 3. Dựa vào bảng xét dấu tính tích phân: . Dạng 5: khi tính diện tích giới hạn 3 hàm số trở lên thì phương pháp chung là vẽ đồ thị rồi dựa vào đồ thị để tính. Cách tính giới hạn của 3 hàm số: Cho 3 hàm số , và liên tục trên . Khi đó diện tích của hình phẳng (H) giới hạn bởi đồ thị 3 hàm số , và là: Với: + là nghiệm phương trình: + là nghiệm phương trình: + là nghiệm phương trình: Trong đó: Tóm lại khi giải toán ta thường gặp các dạng sau: 1. Diện tích S của miền giới hạn: 2. Diện tích S của miền giới hạn: 3. Diện tích S của miền giới hạn: DẠNG 1 TÍNH DIỆN TÍCH HÌNH PHẲNG Cho hàm số liên tục trên đoạn và cắt trục hoành tại điểm (như hình vẽ). Gọi là diện tích hình phẳng giới hạn bởi đồ thị của hàm số , trục hoành và hai đường thẳng . Trong các khẳng định sau, khẳng định nào là khẳng định đúng? A. B. C. D. Cho đồ thị hàm số . Diện tích hình phẳng (phần có đánh dấu gạch trong hình) là: A. B. C. D. Gọi là diện tích hình phẳng giới hạn bởi các đường trục hoành và hai đường thẳng (như hình vẽ). Đặt Mệnh đề nào sau đây đúng? A. B. C. D. Cho đồ thị hàm số . Diện tích hình phẳng (phần tô đậm trong hình) là: A. B. C. D. Cho đồ thị hàm số . Diện tích hình phẳng (phần gạch trong hình) là: A. B. C. D. Cho đồ thị hàm số . Diện tích hình phẳng (phần gạch chéo trong Hình 1) là: A. B. C. D. Cho đồ thị hàm số . Diện tích của hình phẳng (phần tô đậm trong hình dưới) là: A. . B. . C. . D. . Cho hàm số có đồ thị như hình vẽ dưới đây. Diện tích hình phẳng (phần tô màu trong hình vẽ) được tính bằng công thức nào A. B. C. D. Cho hình phẳng giới hạn bởi các đường . Đường thẳng chia hình thành hai phần có diện tích (hình vẽ). Tìm để A. B. C. D. Tính diện tích hình phẳng giới hạn bởi các đường , và trục hoành như hình vẽ. A. . B. . C. . D.. Cho hàm số liên tục trên , đồ thị hàm số như hình vẽ. Diện tích các hình phẳng A, B lần lượt là và . Biết , tính A. B. C. D. Tính diện tích của phần hình phẳng giới hạn bởi đường Parabol đi qua gốc toạ độ và hai đoạn thẳng và như hình vẽ bên ? A.. B.. C.. D.. Cho đồ thị hàm số trên đoạn như hình vẽ và có diện tích . Tính tích phân A. B. C. D. Diện tích hình phẳng giới hạn bởi các đường và là: A. B. C. D. Tìm d để diện tích hình phẳng giới hạn bởi đường cong , Ox, x =1, x = d (d >1) bằng 2: A. B. e C. 2e D. e+1 Diện tích hình phẳng giới hạn bởi đường thẳng và parabol bằng: A. B. C. D. Cho Parabol y = x2 và tiếp tuyến At tại A(1 ; 1) có phương trình: y = 2x – 1. Diện tích của phần bôi đen như hình vẽ là:y x A 1 -1 -1 -2 4 1 A. B. C. D. Một số khác Cho ba đồ thị: và như hình vẽ: Diện tích hình phẳng giới hạn bởi ba đồ thị trên (phần gạch trong hình) là: A. . B. . C. . D. . Tính diện tích của phần hình phẳng gạch sọc (bên dưới) giới hạn bởi đồ thị hàm số bậc ba và trục hoành. A.. B.. C.. D.. Cho hàm số có đồ thị cắt trục Ox tại ba điểm có hoành độ như hình vẽ. Mệnh đề nào dưới đây là đúng? A. B. C. D. Cho đồ thị hàm số trên đoạn như hình vẽ ở bên và có diện tích . Tính tích phân A. B. C. D. Cho hình phẳng giới hạn bởi các đường và Tìm để diện tích của hình phẳng gấp hai lần diện tích hình phẳng được kẻ sọc trong hình vẽ bên. A. B. C. D. Cho hình thang cong (H) giới hạn bởi các đường và . Đường thẳng chia (H) thành hai phần có diện tích và như hình vẽ bên. Tìm k để . A. . B. . C. . D. . Cho hàm số có đồ thị với là tham số thực. Giả sử cắt trục tại bốn điểm phân biệt như hình vẽ : Gọi , và là diện tích các miền gạch chéo được cho trên hình vẽ. Tìm để . A. . B. . C. . D. . Parabol chia hình tròn có tâm là gốc tọa độ, bán kính bằng thành hai phần có diện tích là và , trong đó . Tìm tỉ số A. B. C. D. Gọi là diện tích của mặt phẳng giới hạn bởi đường thẳng với m < 2 và parabol (P) có phương trình . Gọi là diện tích giới hạn bởi (P) và Ox. Với trị số nào của m thì ? A. . B. . C. . D. . Cho hàm số có đồ thị . Biết rằng đồ thị tiếp xúc với đường thẳng tại điểm có hoành độ âm và đồ thị hàm số cho bởi hình vẽ dưới đây: Tính diện tích của hình phẳng giới hạn bởi đồ thị và trục hoành. A. . B. . C. . D. . Gọi là hình phẳng giới hạn bởi đồ thị hàm số: , trục tung và trục hoành. Xác định để đường thẳng đi qua điểm có hệ số góc chia thành hai phần có diện tích bằng nhau. A. . B. . C. . D. . Cho hai hàm số có đồ thị và liên tục trên . Diện tích hình phẳng giới hạn bởi và hai đường thẳngđược tính bởi công thức: A. B. C. D. Cho và là hai hàm số liên tục trên đoạn [a;b]. Giả sử: và , với , là các nghiệm của phương trình . Khi đó diện tích của hình phẳng giới hạn bởi 2 đường thẳng và đồ thi của hàm số được cho bởi công thức: hoặc Nhận xét nào sau đây đúng nhất? A. đúng nhưng sai. B. đúng nhưng sai. C. Cả và đều đúng. D. Cả và đều sai. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 2 – x2 và y = x. A. 5 B. 7 C. D. Gọi là diện tích hình phẳng giới hạn bởi các đường , và . Mệnh đề nào sau đây là đúng? A. B. C.. D. Cho hàm số liên tục trên . Gọi là hình phẳng giới hạn bởi các đồ thị hàm số và Công thức tính diện tích của là công thức nào trong các công thức dưới đây? A. B. C. D. Diện tích hình phẳng giới hạn bởi đường cong và trục hoành là: A. B. C. D. Tính diện tích hình phẳng giới hạn bởi hai đường cong và . A. B. C. D. Tính diện tích S của hình phẳng giới hạn bởi các đường A. B. C. D. Gọi S là diện tích hình phẳng giới hạn bởi các đường . Khẳng định nào sau đây đúng? A. B. C. D. Diện tích hình phẳng giới hạn bởi hàm số , trục và hai đường thẳng bằng với . Khi đó giá trị của thuộc khoảng nào sau đây? A. . B. . C. . D. . Diện tích hình phẳng giới hạn bởi hàm số và bằng với . Khi đó giá trị của thuộc khoảng nào sau đây? A. . B. . C. . D. . Diện tích hình phẳng giới hạn bởi hàm số bằng với . Khi đó giá trị của thuộc khoảng nào sau đây? A. . B. . C. . D. Diện tích hình phẳng giới hạn bởi hàm số bằng với . Khi đó giá trị của thuộc khoảng nào sau đây? A. . B. . C. . D. Tính diện tích hình phẳng tạo bởi các đường: Parabol và 2 tiếp tuyến tại các điểm nằm trên . A. B. C. D. Diện tích hình phẳng giới hạn bởi hàm số và trục hoành bằng với . Khi đó giá trị của thuộc khoảng nào sau đây? A. . B. . C. . D. Diện tích hình phẳng giới hạn bởi hàm số và trục Ox và đường thẳng bằng với . Khi đó giá trị của thuộc khoảng nào sau đây? A. . B. . C. . D. Diện tích hình phẳng giới hạn bởi các đường: và trục Ox bằng với . Khi đó giá trị của thuộc khoảng nào sau đây? A. . B. . C. . D. Gọi là diện tích hình phẳng giới hạn bởi các đường và . Giá trị cần tìm là: A.. B. . C. . D. . Diện tích hình phẳng giới hạn bởi các đường , trục hoành và hai đường thẳng , nhận giá trị nào sau đây: A. . B. . C. . D. . Diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành, trục tung và đường thẳng là: A. B. C. D. Diện tích hình phẳng giới hạn bởi các đường , và là: A. . B. . C. . D. . Diện tích hình phẳng giới hạn bởi các đường và trục Ox được tính bởi công thức A. B. C. D. Diện tích hình phẳng giới hạn bởi parabol , tiếp tuyến với nó tại điểm và trục là giá trị nào sau đây? A. . B. . C.. D.. Cho hàm số có đồ thị . Phương trình tiếp tuyến của tại điểm có hoành độ bằng có đồ thị . Gọi là diện tích hình phẳng giới hạn bởi đồ thị , đường thẳng và trục tung. Giá trị củalà: A.. B.. C.. D.. Diện tích hình phẳng giới hạn bởi đồ thị hàm số đường thẳng , đường thẳng và trục tung được tính như sau: A. . B. C. D. Diện tích của hình phẳng giới hạn bởi hai đường cong có phương trình và bằng: A. B. . C. D. Với giá trị nào của để diện tích của hình phẳng giới hạn bởi , đường tiệm cận xiên của và hai đường thẳng bằng ? A. . B. . C. . D. . Kết quả của diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành, trục tung và đường thẳng có dạng (với là phân số tối giản). Khi đó mối liên hệ giữa và là: A. B. . C. D. Diện tích hình phẳng giới hạn bởi hàm số , trục và đường thẳng bằng với , , là các số nguyên dương. Khi đó giá trị của là A. . B. . C. . D. . Cho hình phẳng giới hạn bởi các đường trục hoành, trục tung và đường Tìm giá trị của để đường thẳng chia hình phẳng thành hai phần có diện tích bằng nhau A. B. C. . D. DẠNG 2 ỨNG DỤNG THỰC TẾ DIỆN TÍCH HÌNH PHẲNG Một sân chơi dành cho trẻ em hình chữ nhật có chiều dài và chiều rộng là người ta làm một con đường nằm trong sân (như hình vẽ). Biết rằng viền ngoài và viền trong của con đường là hai đường elip và chiều rộng của mặt đường là . Kinh phí để làm mỗi làm đường đồng. Tính tổng số tiền làm con đường đó. (Số tiền được làm tròn đến hàng nghìn) A. . B. . C. . D. . Một sân chơi cho trẻ em hình chữ nhật có chiều dài và chiều rộng là , người ta làm một con đường nằm trong sân (Như hình vẽ). Biết rằng viền ngoài và viền trong của con đường là hai đường elip, Elip của đường viền ngoài có trục lớn và trục bé lần lượt song song với các cạnh hình chữ nhật và chiều rộng của mặt đường là . Kinh phí cho mỗi làm đường đồng. Tính tổng số tiền làm con đường đó. (Số tiền được làm tròn đến hàng nghìn). A. B. C. D. Một khuôn viên dạng nửa hình tròn ... nh khi quay hình (H) (phần tô đậm) xung quanh đường thẳng AB. A.. B.. C.. D.. Một vật có kích thước và hình dáng như hình vẽ dưới đây. Đáy là hình tròn bán kinh 4 cắt vật bởi các mặt phẳng vuông góc với trục Ox ta được thiết diện là tam giác đều. Thể tích của vật thể là: A. B. C. D. Một vật có kích thước và hình dáng như hình vẽ dưới đây. Đáy là hình tròn giới hạn bởi đường tròn (nằm trong mặt phẳng Oxy), cắt vật bởi các mặt phẳng vuông góc với trục Ox ta được thiết diện là tam giác đều. Thể tích của vật thể là: A. B. C. D. Một thùng đựng nước có dạng hình trụ có chiều cao h và bán kính đáy bằng R. Khi đặt thùng nước nằm ngang như hình 1 thì khoảng cách từ trục hình trụ tới mặt nước bằng (mặt nước thấp hơn trục của hình trụ). Khi đặt thùng nước thẳng đứng như hình 2 thì chiều cao của mực nước trong thùng là . Tính tỉ số . A. B. C. D. Một khối nón (N) có bán kính đáy r, thiết diện qua đỉnh và vuông góc với mặt đáy là tam giác đều. Cắt hình nón bởi mặt phẳng đi qua đường kính đáy và vuông góc với đường sinh của khối nón để lấy một cái nêm (xem hình vẽ).Kí hiệu V là thể tích cái nêm. Thể tích V là? A. B. C. D. Cho một khối chỏm cầu (S) có bán kính R và chiều cao h. Tính thể tích V của khối chỏm cầu (S). A. B. . C. . D. . Một hình xuyến dạng cái phao có kích thước như hình vẽ. Tính thể tích của hình đó theo R và r. A. B. C. D. Cho hình vuông ABCD có cạnh 4cm. Tại bốn đỉnh A, B, C, D người ta vẽ lần lượt bốn đường tròn có bán kính bằng nhau và bằng Tính thể tích phần được tô màu khi quay hình phẳng xung quanh trục XY. A. B.. C. . D. . Câu lạc bộ bóng đá Manchester United dự định xây dựng SVĐ mới có tên là Old trafford. Hệ thống mái của SVĐ dự định được xây dựng có dạng hai hình elip như hình bên với hình elip lớn bên ngoài có độ dài trục lớn là 146 mét, độ dài trục nhỏ là 108 mét, hình elip nhỏ bên trong có độ dài trục lớn là 110mét, độ dài trục nhỏ là 72 mét. Giả sử chi phí vật liệu là 100 đôla mỗi mét vuông. Tính chi phí cần thiết để xây dựng hệ thống mái sân. A.98100 đôla . B. 98100 đôla . C.196200 đôla. D.196200 đôla. Người ta dựng một cái lều vải (H) có dạng hình “chóp lục giác cong đều” như hình vẽ bên. Đáy của hình (H) là một hình lục giác đều cạnh 3m. Chiều cao SO = 6m (SO vuông góc với mặt phẳng đáy). Các cạnh bên của (H) là các sợi dây nằm trên các đường parabol có trục đối xứng song song với SO. Giả sử giao tuyến (nếu có) của (H) với mặt phẳng (P) qua trung điểm của SO thì lục giác đều có cạnh 1m. Tính thể tích phần không gian nằm bên trong cái lều (H) đó. A. . B. . C.. D.. CHỦ ĐỀ 3 BÀI TOÁN LIÊN QUAN ĐẾN CHUYỂN ĐỘNG Giả sử là vận tốc của vật tại thời điểm và là quãng đường vật đi được sau khoảng thời gian tính từ lúc bắt đầu chuyển động. Ta có mối liên hệ giữa và như sau: ● Đạo hàm của quãng đường là vận tốc: ● Nguyên hàm của vận tốc là quãng đường từ đây ta cũng có quãng đường vật đi được trong khoảng thời gian là Nếu gọi là gia tốc của vật thì ta có mối liên hệ giữa và như sau: ● Đạo hàm của vận tốc là gia tốc: . ● Nguyên hàm của gia tốc là vận tốc: Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh; từ thời điểm đó, ôtô chuyển động chậm dần đều với vận tốc (m/s), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét ? A. . B. . C.. D. . Một vật chuyển động chậm dần với vận tốc Quãng đường vật di chuyển được thời điểm đến thời điểm mà vật dừng lại là A. B. C. D. Một ô tô đang chuyển động đều với vận tốc 10 (m/s) thì người lái đạp phanh; từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc (m/s) (trong đó t là thời gian tính bằng giây, kể từ lúc đạp phanh). Hỏi trong thời gian 7 giây cuối (tính đến khi xe dừng hẳn) thì ô tô đi được quảng đường bằng bao nhiêu? A. B. C. D. Một ô tô đang chạy với vận tốc thì tăng tốc chuyển động nhanh dần đều với gia tốc tính quãng đường ô tô đi được sau 6 giây kể từ khi ô tô bắt đầu tăng tốc. A. B. C. D. Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật trong đó (phút) là thời gian tính từ lúc bắt đầu chuyển động, được tính theo đơn vị mét/phút (m/p). Nếu như vậy thì khi bắt đầu tiếp đất vận tốc của khí cầu là: A. B. C. D. Một ô tô đang chạy với vận tốc 12m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến khi ô tô dừng hẳn, ô tô còn di chuyển được bao nhiêu mét ? A.. B.. C.. D.. Một vật chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc được tính theo thời gian t là . Tính quảng đường vật đi được trong khoảng 10s kể từ khi bắt đầu tăng tốc. A.. B.. C.. D.. Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu là , gia tốc trọng trường là . Quảng đường viên đạn đi được từ lúc bắn cho đến khi chạm đất gần bằng kết quả nào nhất trong các kết quả sau: A. . B.. C. . D. . Một ca nô đang chạy trên hồ Tây với vận tốc thì hết xăng; từ thời điểm đó, ca nô chuyển động chậm dần đều với vận tốc , trong đó là khoảng thời gian tính bằng giây, kể từ lúc hết xăng. Hỏi từ lúc hết xăng đến lúc ca nô dừng hẳn đi được bao nhiêu mét? A.. B.20. C.30. D.40. Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc Đi được , người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc Tính quãng đường đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn. A. . B. . C. . D. . Một vật chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc được tính theo thời gian t là . Tính quảng đường vật đi được trong khoảng 10s kể từ khi bắt đầu tăng tốc. A.. B.. C.. D.. Một chiếc xe đang chạy với vận tốc 100Km/h thì đạp phanh dừng lại, vận tốc của xe giảm dần theo công thức (Km/h) cho đến khi dừng lại. Hỏi xe chạy thêm được bao nhiêu met thì dừng lại. A. 25 B. 1 C. 103 D. 10-3 Khi quan sát một đám vi khuẩn trong phòng thí nghiệm người ta thấy tại ngày thứ x có số lượng là . Biết rằng và lúc đầu số lượng vi khuẩn là 5000 con .Vậy ngày thứ 12 số lượng vi khuẩn là? A. 10130. B. 5130. C. 5154. D. 10129. Một vật chuyển động với vận tốc 10 m/s thì tăng tốc với gia tốc . Tính quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc. A. B. C. D. Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu là và gia tốc trọng trường là . Quãng đường viên đạn đi từ lúc bắn lên cho tới khi rơi xuống đất là (coi như viên đạn được bắn lên từ mặt đất) A. B. C. D. Một bác thợ xây bơm nước vào bể chứa nước. Gọi h(t) là thể tích nước bơm được sau t giây. Cho và ban đầu bể không có nước. Sau 5 giây thì thể tích nước trong bể là . Sau 10 giây thì thể tích nước trong bể là . Hỏi thể tích nước trong bể sau khi bơm được 20 giây là bao nhiêu. A. B. C. D. Một người đứng từ sân thượng một tòa nhà cao 262m, ném một quả bi sắt theo phương thẳng đứng hướng xuống (bỏ qua ma sát) với vận tốc 20m/s. Hỏi sau 5s thì quả bi sắt cách mặt đất một đoạn bao nhiêu mét? (Cho gia tốc trọng trường ) A. 35 m B.36 m C. 37 m D. 40 m Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt vận tốc 6m/s. Từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B cũng xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động thẳng nhanh dần đều. Biết rằng B đuổi kịp A sau 8 giây (kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A.12m/s. B.48m/s. C.24m/s. D.36m/s. Bạn Minh ngồi trên máy bay đi du lịch thế giới với vận tốc chuyển động của máy báy là. Quãng đường máy bay bay từ giây thứ 4 đến giây thứ 10 là: A. 36m . B.252m. C.1134m. D.966m. Gọi (cm) là mực nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 6 giây (làm tròn kết quả đến hàng phần trăm). A. 2.66( cm). B.0,55(cm). C.3,14(cm ). D.2,66( cm). Một ô tô đang chạy với vận tốc 20 / (m s) thì người người đạp phanh. Sau khi đạp phanh, ô tô chuyển động chậm dần đều với vận tốc , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bằng đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A. 5( cm). B.7,5(m). C. (m ). D.5( m). Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc . Đi được , người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc . Tính quãng đường đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn. A. B. C. D. Trong một đợt xả lũ, nhà máy thủy điện đã xả lũ trong 40 phút với tốc độ lưu lượng nước tại thời điểm giây là . Hỏi sau thời gian xả lũ trên thì hồ thoát nước của nhà máy đã thoát đi một lượng nước là bao nhiêu? A.. B.. C.. D.. Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật , trong đó (phút) là thời gian tính từ lúc bắt đầu chuyển động, được tính theo đơn vị mét/phút (). Nếu như vậy thì khi bắt đầu tiếp đất vận tốc của khí cầu là A.. B.. C.. D.. Một dòng điện có điện lượng truyền trong dây dẫn tại thời điểm là , có cường độ là . Tính điện lượng truyền trong dây dẫn từ thời điểm đến . A. B. C. D. Cổng trường ĐHBK Hà nội có hình dạng Parabol, chiều rộng 8m, chiều cao 12,5m. Diện tích của cổng là: A. . B. . C. . D. . Vi khuẩn HP (Helicobacter pylori) gây đau dạ dày tại ngày thứ t với số lượng là F(t), biết nếu phát hiện sớm khi số lượng không vượt quá 4000 con thì bệnh nhân sẽ được cứu chữa. Biết và ban đầu bệnh nhân có 2000 con vi khuẩn. Sau 15 ngày bệnh nhân phát hiện ra bị bệnh. Hỏi khi đó có bao nhiêu con vi khuẩn trong dạ dày (lấy xấp xỉ hàng thập phân thứ hai) và bệnh nhân có cứu chữa được không? A. 5433,99 và không cứu được. B. 1499,45 và cứu được. C. 283,01 và cứu được. D.3716,99 và cứu được. Sự sản sinh vi rút Zika ngày thứ t có số lượng là N(t), biết và lúc đầu đám vi rút có số lượng 250.000 con. Sau 10 ngày số lượng vi rút (lấy gần đúng hàng đơn vị): A. 264.334 con B.257.167 con C.258.959 con D. 253.584 con. Người ta bơm nước vào một bồn chứa, lúc đầu bồn không chứa nước, mức nước ở bồn chứa sau khi bơm phụ thuộc vào thời gian bơm nước theo một hàm số h = h(t) trong đó h tính bằng cm, t tính bằng giây. Biết rằng . Mức nước ở bồn sau khi bơm được 13 giây là A. B. C. D. Một người có mảnh đất hình tròn có bán kính 5m, người này tính trồng cây trên mảnh đất đó, biết mỗi mét vuông trồng cây thu hoạch được giá 100 nghìn. Tuy nhiên cần có khoảng trống để dựng chồi và đồ dùng nên người này căng sợi dây 6m sao cho 2 đầu mút dây nằm trên đường tròn xung quanh mảnh đất. Hỏi người này thu hoạch được bao nhiêu tiền (tính theo đơn vị nghìn và bỏ phần số thập phân). A. B. C. D.
Tài liệu đính kèm:
 de_cuong_on_tap_mon_toan_lop_12_phan_3_ung_dung_cua_tich_pha.docx
de_cuong_on_tap_mon_toan_lop_12_phan_3_ung_dung_cua_tich_pha.docx






