Chuyên đề: Về phương trình tiếp tuyến ( cơ bản )
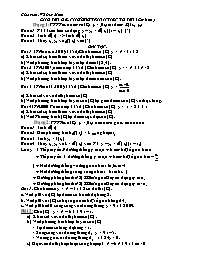
Dạng 1: PTTT của hàm số (C): y = f(x) tại điểm M0(x0; y0)
Bước 1: PTTT cần tìm có dạng: y – y0 = (x0)(x – x0) (*)
Bước 2: Tính (x) => Tính (x0)
Bước 3: Thay x0, y0 và (x0) vào (*)
BÀI TẬP:
Bài 1: (TN bổ túc 2007) (3,5 đ)Cho hàm số (C): y = x3 - 3x + 2
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C)
b) Viết phương trình tiếp tuyến tại điểm I(2; 4).
Bạn đang xem tài liệu "Chuyên đề: Về phương trình tiếp tuyến ( cơ bản )", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
CHUYÊN ĐỀ: PHƯƠNG TRÌNH TIẾP TUYẾN ( Cơ bản ) Dạng 1: PTTT của hàm số (C): y = f(x) tại điểm M0(x0; y0) Bước 1: PTTT cần tìm có dạng: y – y0 = (x0)(x – x0) (*) Bước 2: Tính (x) => Tính (x0) Bước 3: Thay x0, y0 và (x0) vào (*) BÀI TẬP: Bài 1: (TN bổ túc 2007) (3,5 đ)Cho hàm số (C): y = x3 - 3x + 2 a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) b) Viết phương trình tiếp tuyến tại điểm I(2; 4). Bài 2: (TN 2007 phân ban) (3,5 đ )Cho hàm số (C): y = - x3 + 3x2 - 2 a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) b) Viết phương trình tiếp tuyến tại điểm uốn của (C). Bài 3: (TN lần II 2007) (3,5 đ )Cho hàm số (C): y = a) Khảo sát và vẽ đồ thị hàm số (C) b) Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung. Bài 4 (TN2006 Phân ban) (3,5 đ ) Cho hàm số (C): y = x4 - 2x2 + 1 a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) b) Viết Phương trình (C) tại điểm cực đại của (C). Dạng 2: PTTT của (C): y = f(x) biết hệ số góc k cho trước Bước 1: Tính (x) Bước 2: Giải phương trình (x0) = k nghiệm x0 Bước 3: Tính y0 = f(x0) Bước 4: Thay x0, y0 và k = (x0) vào PT: y – y0 = (x0)(x – x0) Lưu ý: + Tieáp tuyeán // ñöôøng thaúng y = a.x + b => heä soá goùc k = a + Tieáp tuyeán ^ ñöôøng thaúng y = a.x + b => heä soá goùc k = - ( + Hai ñöôøng thaúng vuoâng goùc nhau : k1.k2 = -1 + Hai ñöôøng thaúng song song nhau : k1 = k2 ) + Ñöôøng phaân giaùc thö I ; III cuûa goùc Oxy coù daïng: y = x. + Ñöôøng phaân giaùc thö I ; III cuûa goùc Oxy coù daïng: y = - x. Bài 1: Cho hàm số y = x3 – 3x + 2 có đồ thi (C). a. Viết pttt với (C) tại điểm có hoành độ bằng 2. b. Viết pttt với (C) có hệ số goùc coù heä soá goùc baèng 24. c. Viết pttt biết tt song song với đường thẳng y = 9x + 2009. Bài 2: Cho (C) : y = x3 – 6x2 + 9x – 1. Khảo sát và vẽ đồ thị hàm số (C) . Viết phương trình tiếp tuyến của (C) : - Tại điểm có tung độ bằng -1. - Song song với đường thẳng d1 : y = 9x – 5. - Vuông góc với đường thẳng d2 : x + 24y = 0. c) Dựa vào đồ thị biện luận số nghiệm pt: x3 – 6x2 + 9x + m = 0 Bài 3: (TN 2009) (3,0 đ ) Cho hàm số (C): y = a) Khảo sát và vẽ đồ thị hàm số (C) b) Viết phương trình tiếp tuyến của (C) có hệ số góc bằng -5. Bài 4: Cho (C) : y = .Viết phương trình tiếp tuyến của (C): Tại giao điểm của (C ) với trục Ox. Song song với đường thẳng d1 : y = 4x – 5. Vuông góc với đường phân giác thứ II Oxy. Bài 5: Cho hàm số y = có đồ thị ( C ) .Viết phương tŕnh tiếp tuyến của ( C) : a) Tại giao điểm của ( C ) và trục tung . b) Tại điểm có tung độ y = -3 và x < 0 . c) Biết tiếp tuyến vuông góc với đường thẳng y = 24 x +1 Bài 6: Cho hàm số (C): y = x3 – 3x2 + 4 a) Khảo sát và vẽ đồ thị hàm số (C) b) Viết phương trình tiếp tuyến của (C) song song với đường thẳng y = . ĐS: y = ; y = Bài 7: Viết phương tŕnh tiếp tuyến của đồ thị hàm số y = tại giao điểm của nó với trục hoành Bài 2: Cho hàm số y = có đồ thị ( C ) . Viết phương tŕnh tiếp tuyến của ( C) : a/ Tại điểm có hoành độ x0 = b/ Biết tiếp tuyến song song với đường thẳng y = 3x – 1 Bài 7: Cho hàm số (C): y = a) Khảo sát và vẽ đồ thị hàm số (C). b) Viết phương trình tiếp tuyến của (C) vuông góc với đường phân giác phần tư thứ nhất Bài 8: Cho hàm số (C): y = -x3 + 3x + 2 a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) b) Dựa vào đồ thị (C), biện luận theo m số nghiệm của phương trình: x3 – 3x – 1 + m = 0 ĐS: * m > 4: 1 n0; * m = 4: 2 n0; * 0 < m < 4: 3 n0; * m = 0: 2 n0; * m < 0: 1 n0 c) Viết phương trình tiếp tuyến tại điểm I(0; 2). ĐS: y = 3x + 2 d) Viết phương trình đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị (C) HD: PT đt đi qua 2 điểm A(xA; yA) và B(xB; yB) có dạng: . ĐS: y = 2x + 2 Bài 9: Cho hàm số (C): y = x3 + 3x2 + 1 a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) b) Dựa vào đồ thị (C), biện luận theo k số nghiệm của phương trình: x3 + 3x2 – k = 0 ĐS: * k > 4: 1 n0; * k = 4: 2 n0; * 0 < k < 4: 3 n0; * k = 0: 2 n0; * k < 0: 1 n0 c) Viết phương trình tiếp tuyến tại điểm có hoành độ bằng -1 HD: Thế x = -1 vào (C) y = 3: M(-1; 3). ĐS: y = -3x d) Viết phương trình đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị (C) ĐS: y = -2x + 1 Bài 10: Cho hàm số (C): y = x4 – 2x2 – 3 a) Khảo sát và vẽ đồ thị hàm số (C) b) Viết phương trình tiếp tuyến của (C), biết hệ số góc của tiếp tuyến là 24. ĐS: y = 24x – 43 Bài 11: Cho hàm số (C): y = - x4 + 2x2 + 1 a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) b) Biện luận theo m số nghiệm của phương trình: -x4 + 2x2 + 1 – m = 0 ĐS: * m > 2: vô n0; * m = 2: 2 n0; * 1 < m < 2: 4 n0; * m = 1: 3 n0; * m < 1: 2 n0 c) Viết phương trình tiếp tuyến tại điểm có tung độ bằng 2 HD: Thế y = 2 vào (C) x =1: M(-1; 2), N(1; 2). ĐS: y = 2 HD: Đường phân giác phần tư thứ nhất là: y = x. ĐS: y = -x và y = -x + 8 Bài 12: Cho hàm số (Cm): y = 2x3 + 3(m – 1)x2 + 6(m – 2)x – 1 a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) khi m = 2 b) Với giá trị nào của m, đồ thị của hàm số (Cm) đi qua điểm A(1; 4). ĐS: m = 2 c) Viết phương trình tiếp tuyến của hàm số (C) đi qua điểm B(0; -1). ĐS: y = -1; y = Bài 13: Cho hàm số (Cm): y = a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C2) b) Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn đồng biến trên mỗi khoảng xác định của nó HD: Chứng minh tử thức của y’ > 0 suy ra y’ > 0(đpcm) c) Xác định m để tiệm cận đứng của đồ thị đi qua A(-1; ). ĐS: m = 2 d) Viết phương trình tiếp tuyến của hàm số (C2) tại điểm (1; ). Bài 14( Khối D.2005) Cho (Cm): và M (Cm) có hoành độ x = 1. Tìm m để tiếp tuyến của (Cm) tại M là song song với đường thẳng d: 5x – y = 0.
Tài liệu đính kèm:
 PTTiep tuyen Bien luancb.doc
PTTiep tuyen Bien luancb.doc





