Chuyên đề Tích phân ứng dụng - Chủ đề: Thể tích khối tròn xoay

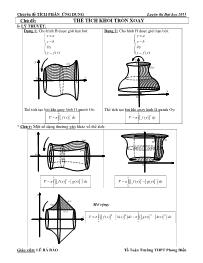
Chuyên đề TÍCH PHÂN_ỨNG DỤNG Luyện thi Đại học 2011 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
 Chủ đề: THỂ TÍCH KHỐI TRÒN XOAY 
I- LÝ THUYẾT: 
Dạng 1: Cho hình H được giới hạn bởi: 
( )
x a
x b
Ox
y f x
=ì
ï =ï
í
ï
ï =î
Dạng 2: Cho hình H được giới hạn bởi: 
( )
y a
y b
Oy
x f y
=ì
ï =ï
í
ï
ï =î
Thể tích tạo bởi khi quay hình H quanh Ox: 
[ ] 2 ( ) d p= ò
b
a
V f x x 
Thể tích tạo bởi khi quay hình H quanh Oy: 
[ ] 2 ( ) d p= ò
b
a
V f y y 
* Chú ý: Một số dạng thường gặp khác về thể tích: 
[ ] [ ]( )2 2 ( ) ( ) d p= -ò
b
a
V f x g x x 
[ ] [ ]( )2 2 ( ) ( ) d p= -ò
b
a
V f y g y y 
 Mở rộng: 
[ ] [ ]( ) [ ] [ ]( )2 2 2 2 ( ) ( ) ( ) ( ) 
c b
a c
V f x h x dx g x h x dxp p= - + -ò ò 
O
y
x
f(x)
ba
a
b
f(y)
O
x
y
g(x)
f(x)
ba
O
y
x
O
y
x
h(x)
g(x)
f(x)
c ba
a
b
f(y)
g(y)
O
y
x
Chuyên đề TÍCH PHÂN_ỨNG DỤNG Luyện thi Đại học 2011 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
II- VÍ DỤ MINH HỌA: 
Ví dụ 1: (TN 03- 04) Cho hình H giới hạn bởi các đường: 3 21 , 0, 0
3
y x x y x= - = = và 3x = . Tính thể 
tích của khối tròn xoay khi quay hình H quanh trục Ox. 
Gợi ý: 
Dựa vào đồ thị, ta có: 
( )
2 23 3
3 2 6 5 4
0 0
5
7 6
1 1 2
d d
3 9 3
31 1 231
 ®.v.t.t
63 9 5 100
HV x x x x x x x
x
x x
p p
p
æ ö æ ö= - = - +ç ÷ ç ÷è ø è ø
æ ö
= - + =ç ÷
è ø
ò ò
Ví dụ 2: (TK- 2007) Cho hình H giới hạn bởi các đường: 24 ,=y x =y x . Tính thể tích của khối tròn 
xoay khi quay hình H quanh trục Ox một vòng. 
Gợi ý: 
Ta có: 
2
24 (P)
4
= Û = xy x y và ( )d : =y x 
Xét phương trình hoành độ giao điểm của (d) và (P): 
 ( )
2 0
4 0
44
=é
= Û - = Û ê =ë
xx x x x
x
Dựa vào đồ thị, ta có: 
( )
( )
24 42 4
2 2
0 0
3 5
d d
4 16
4 64 32 1504
 ®.v.t.t
3 80 3 25 750
H
x x
V x x x x
x x
p p
p
é ùæ ö æ öê ú= - = -ç ÷ ç ÷
ê úè ø è øë û
æ ö
= - = - =ç ÷
è ø
ò ò
Ví dụ 3: Cho hình H giới hạn bởi các đường: 2 / 2(P) : , (P ) : 4y x y x= = và (d): 4y = .Tính thể tích của 
khối tròn xoay khi quay hình H: 
a) quanh trục Ox một vòng. b) quanh trục Oy một vòng. 
Gợi ý : 
a) quanh trục Ox một vòng. 
* Xét phương trình hoành độ giao điểm của (P) và (d): 
 2
2
4
2
x
x
x
=é
= Û ê = -ë
* Xét phương trình hoành độ giao điểm của (P’) và (d): 
 2
1
4 4
1
x
x
x
=é
= Û ê = -ë
Đặt V là thể tích cần tìm. 
 OACV là thể tích khối tròn xoay sinh bởi khi quay ( )
2
H' : 4
y x
y
Oy
ì =
ï =í
ï
î
 quanh Ox. 
x
y
3
d
(C)
O
x
y
4
(P)
d
O
x
y CBA
-1-2 2
4
(P')
O
d(P)
1
Chuyên đề TÍCH PHÂN_ỨNG DỤNG Luyện thi Đại học 2011 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
 OABV là thể tích khối tròn xoay sinh bởi khi quay ( )
24
H'' : 4
y x
y
Oy
ì =
ï =í
ï
î
 quanh Ox. 
Lúc đó: ( ) ( )p pé ù é ù= - = - - -ê ú ê úë û ë ûò ò
2 2
2 22 2
0 0
4 d 4 4 dOAC OABV V V x x x x 
( ) ( )
( )
p p
p p
pp
= - - -
æ ö æ ö
= - - -ç ÷ ç ÷
è ø è ø
æ ö= - - + =ç ÷è ø
ò ò
2 1
4 4
0 0
5 5
 4 d 4 16 d
2 1
 4 4 16.
5 50 0
32 16 4
 8 4 ®.v.t.t
5 5 5
x x x x
x x
x x 
b) quanh trục Oy một vòng. 
Ta có: = = Û =2 / 2 2(P) : , (P ) : 4
4
y
y x y x x 
Đặt V là thể tích cần tìm. 
 OACV là thể tích khối tròn xoay sinh bởi khi quay ( )
( )ì = ³
ïï =í
ï
ïî
 0
H' : 4
x y x
y
Oy
 quanh Oy. 
 OBCV là thể tích khối tròn xoay sinh bởi khi quay ( )
( )
ì
= ³ï
ïï =í
ï
ï
ïî
 0
2
H'' : 4
y
x x
y
Oy
 quanh Oy. 
Lúc đó: ( ) ( )pp p p
é ùæ öê ú= - = - = = =ç ÷ç ÷ê úè øë û
ò ò
2
4 4 22
0 0
43 3
d d 2 ®.v.t.t
2 4 8 0OAC OBC
y y y
V V V y y y 
Ví dụ 4: Hình phẳng (H) là miền trong hình tròn ( )2 24 4x y- + = . Tính thể tích khối tròn xoay khi 
quay hình (H): 
 a) quanh trục Ox một vòng. b) quanh trục Oy một vòng. 
Gợi ý : 
a) quanh trục Ox một vòng. 
Ta có ( )
( )
( )
2 2
2 2
2 2
4 4 8 12
4 4
4 4 8 12
é = - - = - -ê- + = Û ê
= - - - = - - -êë
y x x x
x y
y x x x
x
y
(C)
O
62 41
x
y
BC
A
(P)
d
O
(P')
4
2-2 -1
1
Chuyên đề TÍCH PHÂN_ỨNG DỤNG Luyện thi Đại học 2011 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
Khối tròn xoay sinh ra bởi khi quanh hình phẳng 
28 12
2( ) :
6
y x x
xH
x
Ox
ì = - -
ï
ï =
í
=ï
ïî
 quanh Ox một vòng. 
Lúc đó: ( ) ( ) ( )d d ®.v.t.t
6 6 32
2 2 2
2 2
6 328 12 8 12 4 12
23 3
xV x x x x x x x x pp p p
æ ö
= - - = - - = - - =ç ÷
è øò ò
Nhận xét: Khi quay hình tròn (H) quanh Ox một vòng thì khối tròn xoay nhận được là khối cầu với bán 
kính 2R = . 
 Kiểm tra: ( )mÆt cÇu ®.v.t.t
34 32
3 3
RV p p= = 
b) quanh trục Oy một vòng. 
Đặt V là thể tích cần tìm. 
 ABCDEV là thể tích khối tròn xoay sinh 
bởi khi quay ( )
( )24 4 4
2C' :
2
ì = + - ³
ï
ï =í
= -ï
ïî
x y x
y
y
Oy
 quanh Oy. 
 ABFDEV là thể tích khối tròn xoay sinh 
 bởi khi quay ( )
( )24 4 4
2C :
2
ì = - - £
ï
ï =í
= -ï
ïî
x y x
y
y
Oy
 quanh Oy. 
Lúc đó: ( ) ( )
2 22 2
2 2 2
2 2
4 4 4 4 d 16 4 dp p
- -
é ù= - = + - - - - = -ê úë ûò òABCDE ABFDEV V V y y y y y 
Đặt 
2 : 
22sin d 2cos d 
2 : 
2
p
p
= =
= Þ = Þ
= - = -
x t
y t y t t
x t
Lúc đó: ( )
2 2 2
2 2
2 2 2
16 4 4sin .2cos d 64 cos d 32 1 cos2 d
p p p
p p p
p p p
- - -
= - = = +ò ò òV t t t t t t t 
 ( ) ( )2 16 2 sin 2 32 ®.v.t.t
2
p
p p
p
= + =
-
t t 
x
y
F
E D
A
B
C
(C'')
(C')
-2
2
O
2 41
Chuyên đề TÍCH PHÂN_ỨNG DỤNG Luyện thi Đại học 2011 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
III- BÀI TẬP TỰ LUYỆN: 
Bài 1: Cho miền D giới hạn bởi các đường : ; 2 ; 0y x y x y= = - = 
 Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Oy 
Bài 2: Cho miền D giới hạn bởi hai đường : 2( 2)y x= - và y = 4 
 Tính thể tích khối tròn xoay được tạo nên do D quay quanh: 
 a) Trục Ox 
 b) Trục Oy 
Bài 3: Cho miền D giới hạn bởi hai đường : 2 24 ; 2y x y x= - = + . 
 Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox 
Bài 4: Cho miền D giới hạn bởi các đường : 
2
2
1 ; 
1 2
xy y
x
= =
+
 Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox 
Bài 5: Cho miền D giới hạn bởi các đường y = 2x2 và y = 2x + 4 
 Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox 
Bài 6: Cho miền D giới hạn bởi các đường y = y2 = 4x và y = x 
 Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox 
Bài 7: Cho miền D giới hạn bởi các đường y = 22
1
.
x
ex ; y = 0 ; x= 1 ; x = 2 
 Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox 
Bài 8: Cho miền D giới hạn bởi các đường y = xlnx ; y = 0 ; x = 1 ; x = e 
 Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox 
Bài9: Cho miền D giới hạn bởi các đường y = x )1ln( 3x+ ; y = 0 ; x = 1 
 Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox 
Bài 10: 
1) 
î
í
ì
=
-=
4
)2( 2
y
xy
quay quanh trôc a) 0x; b) 0y 
2) 
î
í
ì
=
==
4
4, 22
y
xyxy
quay quanh trôc a) 0x; b) 0y 
3) 
ïî
ï
í
ì
===
+
=
1,0,0
1
1
2
xxy
x
y
 quay quanh trôc a) 0x; b) 0y 
4) 
î
í
ì
=
-=
0
2 2
y
xxy
 quay quanh trôc a) 0x; b) 0y 
5) 
ïî
ï
í
ì
==
=
=
exx
y
xxy
;1
0
ln.
 quay quanh trôc a) 0x; 
6) (D) 
ï
î
ï
í
ì
=
+-=
>=
1
103
)0(2
y
xy
xxy
 quay quanh trôc a) 0x b) Oy 
7) 
ïî
ï
í
ì
=
=
xy
xy 2
 quay quanh trôc a) 0x; 
8) MiÒn trong h×nh trßn (x - 4)2 + y2 = 1 
quay quanh trôc a) 0x; b) 0y 
9) MiÒn trong (E): 1
49
22
=+
yx
 quay quanh trôc a) 0x; b) 0y 
10) 0
1,;0 1
xy xe
y
x x
ì =
ï =í
ï = £ £î
quay quanh trôc 0x; 
11) 
ï
ï
î
ï
ï
í
ì
==
=
+=
pp xx
y
xxy
;
2
0
sincos 44
quay quanh trôc 0x; 
12) 
î
í
ì
-=
=
xy
xy
310
2
quay quanh trôc 0x; 
Chuyên đề TÍCH PHÂN_ỨNG DỤNG Luyện thi Đại học 2011 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
13) H×nh trßn t©m I(2;0) b¸n kÝnh R = 1 
 quay quanh trôc a) 0x; b) 0y 
14) 
4
4
0; 2
y
x
x x
ì =ï
-í
ï = =î
quay quanh trôc 0x; 
15) 
ï
î
ï
í
ì
==
=
-=
0;0
2
1
yx
y
xy
 quay quanh trôc a) 0x; b) 0y 
16) 
0
4
2 2
y
x
y x
ì =
ï
=í
ï = -î
 quay quanh Ox 
17) 
1
2
4
xy
y
y
=ì
ï =í
ï =î
 quay quanh Oy 
18) 
2
0
1; 1
2
x
y y
x y y
ì =
ï = - =í
ï = - -î
 quay quanh Oy 
19) 
2
2
0
y x
x
y
ì =
ï =í
ï =î
 quay quanh trôc a) 0x; b) 0y