Chuyên đề Nguyên hàm Tích phân - Chủ đề: Diện tích hình phẳng

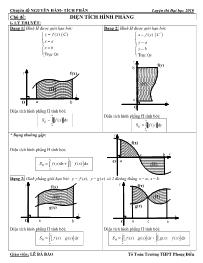
Chuyên đề NGUYÊN HÀM- TÍCH PHÂN Luyện thi Đại học 2010 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
Chủ đề: DIỆN TÍCH HÌNH PHẲNG 
I- LÝ THUYẾT: 
Dạng 1: Hình H được giới hạn bởi: 
( )( ) 
Trôc O
=ì
ï
=ï
í
=ï
ïî
y f x C
x a
x b
x
Dạng 2: Hình H được giới hạn bởi: 
( )/( ) 
Trôc O
ì =
ï
ï =
í
=ï
ïî
x f y C
y a
y b
y
Diện tích hình phẳng H tính bởi: 
 ( ) d = ò
b
H
a
S f x x 
Diện tích hình phẳng H tính bởi: 
 ( ) d = ò
b
H
a
S f y y 
* Dạng thường gặp: 
Diện tích hình phẳng H tính bởi: 
 [ ] ( )d ( ) d = + -ò ò
c b
H
a c
S f x x f x x 
Dạng 3: Hình phẳng giới hạn bởi: ( )=y f x , ( )=y g x và 2 đường thẳng , = =x a x b . 
Diện tích hình phẳng H tính bởi: 
 [ ] ( ) ( ) d = -ò
b
H
a
S f x g x x 
Diện tích hình phẳng H tính bởi: 
[ ] [ ] ( ) ( ) d ( ) ( ) d = - + -ò ò
c b
H
a c
S f x g x x g x f x x 
(H)
O
f(x)y
x
ba
(H)
O
a
b
y
x
f(y)
(H)
c
f(x)
a
b y
x
O
(H)
g(x)
O a b
f(x)
x
y
(H)
ca b
g(x)
f(x)y
O
x
Chuyên đề NGUYÊN HÀM- TÍCH PHÂN Luyện thi Đại học 2010 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
Lưu ý: 
1- Trong rất nhiều bài toán, giả thiết ban đầu không có các cận. Vậy thì dễ thấy cận của tích phân 
cần tính là nghiệm của phương trình: ( ) ( )f x g x= 
2- Trong một số trường hợp tính diện tích hình phẳng bằng tích phân theo biến y ta có lời giải 
ngắn gọn, dể hiểu hơn nhiều so với tính tích phân theo biến x . 
Nhận xét: 
a) Dễ nhận thấy, công thức (*) là trường hợp đặc biệt đối với công thức (**) khi ( ) 0g x º . 
b) Như vậy, việc tính diện tích hình phẳng lại quy về việc tính tích phân của hàm số chứa dấu giá trị 
tuyệt đối. Ta làm rõ kỹ năng này. 
 Phương pháp 1: Tìm cận trung gian và lập bảng xét dấu. 
ĐỐI VỚI DẠNG 2: 
 Phương pháp 2: Dùng hình vẽ, với nhận xét: 
[ ] [ ]
( ) ( ) d
 ( ) ( ) d ( ) ( ) d
 ( ) ( ) d ( ) ( ) d
= -
= - + -
= - + -
ò
ò ò
ò ò
b
H
a
c b
a c
c b
a c
S f x g x x
f x g x x f x g x x
f x g x x g x f x x
Phương pháp 2: THUẬT TOÁN TÍNH: ( ) ( ) d = -ò
b
H
a
S f x g x x 
 Bước 1: Giải phương trình ( ) ( )f x g x= .Giả sử có hai nghiệm ( )1 2 1 2, x x a x x b< < < 
 Bước 2: Như vậy trên các đoạn [ ] [ ] [ ]1 1 2 2; , ; , ;a x x x x b thì ( ) ( )f x g x- không đổi dấu: 
 Tức là: 
[ ] [ ] [ ]
1 2
1 2
1 2
1 2
( ) ( ) d ( ) ( ) d ( ) ( ) d ( ) ( ) d
 ( ) ( ) d ( ) ( ) d ( ) ( ) d
= - = - + - + -
= - + - + -
ò ò ò ò
ò ò ò
x xb b
H
a a x x
x x b
a x x
S f x g x x f x g x x f x g x x f x g x x
f x g x x f x g x x f x g x x
II- VÍ DỤ MINH HỌA: 
Ví dụ 1: (Khối A- 2002) Tính diện tích hình phẳng (H) giới hạn bởi các đường sau: 
2 4 3 , 3y x x y x= - + = + 
Gợi ý: Gọi 2(C): 4 3y x x= - + và (d): 3y x= + 
Xét phương trình hoành độ giao điểm của (C) và (d) : 
 2 2 2
2 2
3 3
4 3 3 4 3 3 5 0
4 3 3 3 6 0
x x
x x x x x x x x
x x x x x
³ - ³ -ì ì
ï ïé é- + = + Û Û- + = + - =í í
ê êï ï- + = - - - + =ë ëî î
 (*)
 (1)
 v« nghiÖm
x
y
c
y = g (x )
y = f(x )
ba
O
Chuyên đề NGUYÊN HÀM- TÍCH PHÂN Luyện thi Đại học 2010 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
Ta có : 2
0
5 0
5
x
x x
x
=é
- = Û ê =ë
 Tháa (*)
 Tháa (*)
Cách 1: Dùng đồ thị. 
Dựa vào hình vẽ, ta thấy: [ ]2 4 3 3 0;5x x x x- + £ + " Î 
Lúc đó: 
( )
5
2
0
3 4 3HS x x x x= + - - +ò d
( ) ( ) ( )
( ) ( ) ( )
1 3 5
2 2 2
0 1 3
1 3 5
2 2 2
0 1 3
3 2 3 3 3 2
3 4 3 3 4 3 3 4 3
5 3 6 5
1 3 51 5 1 3 1 5 1096
0 1 33 2 3 2 3 2 6
x x x x x x x x x x x x
x x x x x x x x x
x x x x x x x
= + - + - + + + - + + + - + -
= - + + - + + - +
æ ö æ ö æ ö= - + + - + + - + =ç ÷ ç ÷ ç ÷è ø è ø è ø
ò ò ò
ò ò ò
d d d
d d d
 (®.v.d.t)
Cách 2: Sử dụng chia khoảng 
x 0 1 3 5 
2 4 3x x- + + 0 - 0 + 
Ta có: 
( )
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
5 5
2 2
0 0
1 3 5
2 2 2
0 1 3
1 3 5
2 2 2
0 1 3
1 3 5
2 2 2
0 1 3
3 4 3 3 4 3
3 4 3 3 4 3 3 4 3
3 4 3 3 4 3 3 4 3
1095 3 6 5
6
HS x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x x x x
x x x x x x x x x
= + - - + = + - - +
= + - - + + + - - + + + - - +
= + - + - + + + - + + + - + -
= - + + - + + - + =
ò ò
ò ò ò
ò ò ò
ò ò ò
d d
 d d d
 d d d
 d d d (®.v.d.t)
Nhận xét: Cách giải 1, tỏ ra hiệu quả hơn cách giải 2. 
Ví dụ 2: Tính diện tích hình phẳng (H) giới hạn bởi các đường sau: 
2 5 0, 3 0+ - = + - =y x x y 
Gợi ý: Gọi 2(C): 5x y= - và (d): 3x y= - 
Cách 1: Tính tích phân theo biến y 
Xét phương trình hoành độ giao điểm của (C) và (d) : 
 2 2
1
(C): 5 3 2 0
2
y
y y y y
y
= -é
- = - Û - - = Û ê =ë
Dựa vào hình vẽ ta có: 
x
y
O
(C)
d
2
1
-1
31 5
8
3
x
y
O
4
-1
2(C)
d
1
Chuyên đề NGUYÊN HÀM- TÍCH PHÂN Luyện thi Đại học 2010 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
( ) ( )
2 2 3 2
2 2
1 1
2
5 3 2 2
13 2
8 1 1 7 17 372 4 2
3 3 2 3 2 6
d d
 (®.v.d.t)
- -
æ öé ù= - - - = - + + = - + +ç ÷ë û -è ø
-æ ö æ ö= - + + - - + - = + =ç ÷ ç ÷è ø è ø
ò òH y yS y y y y y y y
Cách 2: Tính tích phân theo biến x 
Xét phương trình hoành độ giao điểm của (C) và (d) : 
 2 2
1 4
(C): 5 3 2 0
2 1
y x
y y y y
y x
= - Þ =é
- = - Û - - = Û ê = Þ =ë
Ta có: 2
5 (PhÇn (C) phÝa trªn Ox)
5 0
5 (PhÇn (C) phÝa d­íi Ox)
é = -
+ - = Û ê
= - -êë
y x
y x
y x
Lúc đó: 
( ) ( )
4 5
1 4
37
5 3 d 5 5 d ... (®.v.d.t)
6
é ù= - - - + - + - = =ë ûò òHS x x x x x x 
Ví dụ 3:(Khối B 2002) Tính diện tích hình phẳng (H) giới hạn bởi các đường sau: 
2 2
4 ,
4 4 2
x xy y= - = 
Gợi ý: Gọi 
2
(E): 4
4
xy = - và 
2
(P): 
4 2
xy = . 
Xét phương trình hoành độ giao điểm của (E) và (P): 
2 2 4 2
2 2 24 4 0 8
4 32 44 2 2 2
xx x x x x
x
é =
- = Û + - = Û = Û ê
= -êë
Trên 2 2;2 2é ù-ë û thì 
2 2
4
4 4 2
x x
- ³ và do hình đối xứng qua trục tung nên: 
2 2 2 2 2 22 2
2 2
1 2
0 0 0
1
4 d 16 d d
4 4 2 2 2
æ ö
= - - = - - = -ç ÷ç ÷è ø
ò ò òH x xS x x x x x S S 
* Tính 
2 2
2
1
0
16 d= -òS x x . Đặt 
2 2 : 
4sin d 4cos d ; 4
2 2
0 : 0
p
p p = =æ öé ù= Þ = Î - Þç ÷ê úë ûè ø = =
x t
x t x t t t
x t
( )
4 4 4
2 2
1
0 0 0
16 sin .4cos d 16 cos d 8 1 cos2 d 2 4
p p p
pÞ = - = = + = +ò ò òS t t t t t t t . 
* Tính 
2 2 3
2
2
0
1 1 82 2
d .
3 32 2 2 2 0
= = =ò xS x x . 
Vậy 1 2
4
2 (®.v.d.t)
3
p= - = +HS S S 
x
y
O
4
-1
2(C)
d
1
x
y
4
2
-4
2
-2 2 2 2
(P)
(E)
O
Chuyên đề NGUYÊN HÀM- TÍCH PHÂN Luyện thi Đại học 2010 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
Ví dụ 4: Tính diện tích hình phẳng (H) giới hạn bởi ( ) 2P : 4 5y x x= - + và các tiếp tuyến của (P) tại các 
điểm có hoành độ 1, 4x x= = . 
Gợi ý: 
Ta có: / 2 4y x= - . 
* Tại điểm có 
/
1
5
4
(1) 4
y
x
k y
=ì
= Þ í
= =î
thì phương trình tiếp tuyến là : 
( )1d : 5 4( 4) 4 11y x y x- = - Û = - . 
* Tại điểm có 
/
1
2
1
(1) 2
y
x
k y
=ì
= Þ í
= = -î
thì phương trình tiếp tuyến là : 
( )2d : 2 2( 1) 2 4 y x y x- = - - Û = - + 
Ta có: ( ) ( )1 2
15
d d ; 1
6
Cæ öÇ = -ç ÷è ø
. 
Dựa vào đồ thị ta có: 
( ) ( ) ( ) ( )
( ) ( )
15
46
2 2
151
6
15
4 3 36
2 2 2 2
151
6
4 5 2 4 d 4 5 4 11 d
15 4
 2 1 d 8 16 d 4 16 .... (®.v.d.t)6 15
3 3
1 6
HS x x x x x x x x
x x
x x x x x x x x x x
é ù é ù= - + - - + + - + - -ë û ë û
æ ö æ ö
= - + + - + = - + + - + =ç ÷ ç ÷
è ø è ø
ò ò
ò ò
Ví dụ 5: Parabol (P): 2 2y x= chia hình tròn (C) tâm O, bán kính 2 2 theo tỉ số nào? 
Gợi ý: 
( )
( )
( ) ( )
2 2 2
2 2
* Ph­¬ng tr×nh hoµnh ®é giao ®iÓm cña (P): 2 0 vµ (C): 8.
2
2
 2 8 0 2 8 0 2
4 lo¹i
Täa ®é giao ®iÓm lµ: B 2;2 vµ C 2; 2
* Ta tÝnh diÖn tÝch h×nh ph¼ng OAB:
y x x y
y
x
x x x x x y
x
= ³ + =
é =é
= Þê ê+ = ³ Û + - = Û = -ëê
ê = -ë
Þ -
2 2 2
2
1
0 2
8
2 d 8 d
3OAB
S S x x x x I= = + - = +ò ò
x
y
(d2)
(d1)
(P)
O
-1
15
6
5
4
2
C
B
A
1
x
y (C')
(P)
O
2 2
2 221
Chuyên đề NGUYÊN HÀM- TÍCH PHÂN Luyện thi Đại học 2010 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
2 2
2
2
TÝnh 8 d . §Æt 2 2 sin d 2 2 cos d
2 2 : 
2
2 : 
4
I x x x t x t t
x t
x t
p
p
= - = Þ =
= =
Þ
= =
ò
( )
2 2 2
2
4 4 4
1
2
2
2 2 cos .2 2 cos d 8 cos d 4 1 cos2 d 2
8 2
* Do ®ã, 2
3 3
4
* Do tÝnh ®èi xøng qua Ox nªn: 2 2 (®.v.d.t).
3
Gäi lµ diÖn tÝch h×nh trßn (C) 8 (®.v.d.t).
Gäi lµ
OABC OAB
I t t t t t t t
S
S S
S S R
S
p p p
p p p
p
p p
p
p p
Þ = = = + = -
= + - = +
= = +
Þ = =
ò ò ò
2 1
1
2
4 4
 phÇn diÖn tÝch h×nh trßn cßn l¹i 8 2 6 (®.v.d.t).
3 3
4
2 3 23KÕt luËn: VËy parabol chia ®­êng trßn thµnh hai phÇn cã tû sè .
4 9 26
3
S S S
S
S
p p p
p p
pp
æ öÞ = - = - + = -ç ÷è ø
+ +
= =
--
Ví dụ 6: Chứng minh với mọi m thì đường thẳng ( )d : 2y mx= + luôn cắt (P): 2 1y x= + tại 2 điểm 
phân biệt . Hãy xác định m để phần diện tích giới hạn bởi đường thẳng (d) và (P) có diện tích nhỏ nhất. 
Gợi ý: 
2 2
2
1 2
* XÐt ph­¬ng tr×nh hoµnh ®é giao ®iÓm cña (P) vµ (d):
 1 2 1 0 (1)
Ta cã: 4 0 . VËy (d) lu«n c¾t (P) t¹i hai ®iÓm ph©n biÖt.
Gäi hai giao ®iÓm A, B cã hoµnh ®é , : ng
x mx x mx
m m
x x
+ = + Û - - =
D = + > "
( )
( ) ( ) ( ) ( ) ( ) ( )
( )
2
1
3 2
22
1
3 3 2 2 2 2
2 1 2 1 2 1 2 1 2 1 2 1 1 2
2 2 2 2
hiÖm cña pt(1).
* DiÖn tÝch h×nh ph¼ng (H) cÇn t×m lµ:
 2 1 d
3 2
1 1
 2 3 6
3 2 6
1 1
 4. 2 1 3 6
6 6
x
H
x
xx mx
S mx x x x
x
m
x x x x x x x x x x x x m x x
m m m m
æ ö
= + - - = - + +ç ÷
è ø
é ù= - - + - + - = - - + + - + -ë û
é ù= - + + - - =ë û
ò
( )
( )
3 4
4 .
3
4
VËy min khi 0. y.c.b.t
3
m
S m
+ ³ "
= =
Chuyên đề NGUYÊN HÀM- TÍCH PHÂN Luyện thi Đại học 2010 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
III- BÀI TẬP TỰ LUYỆN : 
1) (TK-2006): Tính diện tích hình phẳng giới hạn bới các đường: 2 3, 2 1y x x y x= - + = + 
2) (D-2002): Tính diện tích hình phẳng giới hạn bới các đường: 3 1
1
xy
x
- -
=
-
 và , .Ox Oy 
3) (TK-2002): Tính diện tích hình phẳng giới hạn bởi: 3 21 2 3
3
y x x x= - + và Ox . 
4) (A- 2007) Tính diện tích hình phẳng giới hạn bởi: ( ) ( )1 , 1= + = + xy e x y e x . 
5) (TK-2007) Tính diện tích hình phẳng giới hạn bởi các đường: ( )2
1
0, 
1
-
= =
+
x x
y y
x
6) (TK-2007) Tính diện tích hình phẳng giới hạn bởi các đường: 2 2, 2= = -y x y x 
7) (TK 2002) Tìm 50;
6
m æ öÎç ÷è ø
 sao cho hình phẳng giới hạn bởi đồ thị : 
3 21 12 2
3 3
y x mx x m= + - - - và các đường thẳng 0, 2, 0x x y= = = có diện tích bằng 4. 
7) Tính diện tích hình phẳng giới hạn bởi 
2 3 3( ) :
1
x xc y
x
+ +
=
+
 , tiệm cận xiên của đồ thị hàm số và 
 1x = và 2x = . 
 8) Tính diện tích hình (H) trong các trường hợp sau:
1) (H4):
2
2
y x
x y
ì =ï
í
= -ïî
2) (H5): 2
y x
y 2 x
ì =ï
í
= -ïî
3) (H7):
ln xy
2 x
y 0
x e
x 1
ì =ï
ïï =í
ï =ï
=ïî
4) (H8) : 
2
2
y x 2x
y x 4x
ì = -ï
í
= - +ïî
5) (H9):
2 3 3y x x
2 2
y x
ì = + -ï
í
ï =î
6) (H10):
2y 2y x 0
x y 0
ì - + =
í
+ =î
7) 
ï
î
ï
í
ì
-=
=
)(
2:)(
:)(
Ox
xyd
xyC
8) 
ï
î
ï
í
ì
=D
=
=
1:)(
2:)(
:)(
x
yd
eyC x
9) 
î
í
ì
-=
+=
1
122
xy
xy 
10) 
ïî
ï
í
ì
=+
--=
03
4
2
2
yx
xy 
11) 
ï
î
ï
í
ì
=
=-+
=
0
02
y
yx
xy
12) 
ï
ï
î
ïï
í
ì
+
=
=
2
2
1
1
2
x
y
xy
13) 
î
í
ì
===
=
3,0,
22
yyxy
xy 
14) 
ïî
ï
í
ì
==
==
ex
e
x
yxy
,1
0,ln
15) 
ï
ï
î
ïï
í
ì
==
==
3
;
6
cos
1;
sin
1
22
pp xx
x
y
x
y
16) 24y x x= - ; (p) vµ 
tiÕp tuyÕn cña (p) 
®i qua M(5/6,6) 
17)*** 
ï
î
ï
í
ì
-=
-+-=
-+-=
153
34
56
2
2
xy
xxy
xxy
18) 
ï
ï
ï
î
ïï
ï
í
ì
=
=
=
=
ex
y
x
y
xy
0
1
19) 
2 1
5
y x
y x
ì = -ï
í
= +ïî
20) 
ïî
ï
í
ì
=
=
xy
xy
2
3
Chuyên đề NGUYÊN HÀM- TÍCH PHÂN Luyện thi Đại học 2010 
Giáo viên: LÊ BÁ BẢO Tổ Toán Trường THPT Phong Điền 
21)
23 2
0
y x x
y
ì = - - +ï
í
=ïî
22) 
î
í
ì
-=
+=
xy
xy
4
22 
23)
ï
î
ï
í
ì
=
++=
+-=
1
54
22
2
2
y
xxy
xxy
24) 
2
2
1
7
y x
y x
ì = -ï
í
= - +ïî
25) 
ï
î
ï
í
ì
=-=
=
=
1;2
0
3
xx
y
xy
26) 
ïî
ï
í
ì
==
=
-=
pxx
y
xxy
;0
3
cos2sin
27) 
ïî
ï
í
ì
=
++=
0
23
y
x
xy 
28) 
î
í
ì
+=
+=
2
22
xy
xxy 
29) 
ï
î
ï
í
ì
==
-+=
-=
4;0
63
22
2
2
xx
xxy
xxy
30) 
2 5 6
6
y x x
y
ì = - +ï
í
=ïî
31) 
ï
î
ï
í
ì
=
--=
=
2
12
2
2
2
y
xxy
xy
32) 
2 3 2
2
y x x
y
ì = - +ï
í
=ïî
33)
2 5 6
1
y x x
y x
ì = - +ï
í
= +ïî
34)
2
2
3 2y x x
y x
ì = - +ï
í
= -ïî
35) 
2 4 3
3
y x x
y
ì = - +ï
í
=ïî
36) 
ï
î
ï
í
ì
==
-
=
1;0
62
2
xx
xx
xy
37) 
siny x
y x p
ì =ï
í
= -ïî
38) 
ï
î
ï
í
ì
=
--=
=
8
44
2
2
2
y
xxy
xy
39) 
ï
î
ï
í
ì
=
=++
=
0
0122
22
y
yx
xy
40) 
î
í
ì
=
+=
yx
xy
psin
)1( 2 
41) 
2 1
2
y x
x
ì = -ï
í
=ïî
42) 
2 1
2
x y
x
ì = -ï
í
=ïî
43) 
ï
î
ï
í
ì
=
=
+=
0
sin
)1( 2
x
xy
yx
44) 
ï
ï
î
ïï
í
ì
=
-=
24
4
4
2
2
xy
xy
45) 
ï
ï
ï
î
ï
ï
ï
í
ì
=
-
=
=
=
0;
1
2
1
;0
4
y
x
xy
x
x
46) 
ï
î
ï
í
ì
-==
=
= -
xyx
y
y x
3;0
0
5 2
47) 
ïî
ï
í
ì
=+
=
16
6
22
2
yx
xy
48) 
ï
ï
ï
î
ïï
ï
í
ì
=
=
=
x
y
xy
xy
27
27
2
2
49) 
ïî
ï
í
ì
=
-=
xy
xy
4
)4(
2
32
50)
log
0
1 , 10
10
y x
y
x x
ì
ï =
ï
=í
ï
ï = =
î
51)
ïî
ï
í
ì
=
=
2
2
xay
yax
 (a > 0) 
52)
ï
î
ï
í
ì
££
+=
=
px
xxy
xy
0
sin 2 
53) 
ïî
ï
í
ì
-=
=
22
2
)1(827
2
xy
xy
54) 
2 2
1
25 9
x y
+ = vµ hai 
tiÕp tuyÕn ®i qua 
A(0;15/4)