Chuyên đề: Khảo sát hàm số và các bài toán liên quan (cho học sinh TB và yếu)

CHUYÊN ĐỀ : KHẢO SÁT HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
CÁC KIẾN THỨC CƠ BẢN CẦN NHỚ
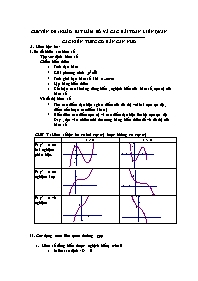
Hàm bậc ba :
I. Sơ đồ khảo sát hàm số
	+ Tập xác định hàm số
	+ Chiều biến thiên
Tính đạo hàm 
Giải phương trình 
Tính giới hạn hàm số khi 
Lập bảng biến thiên
Kết luận các khoảng đồng biến , nghịch biến của hàm số, cực trị của hàm số
+ Vẽ đồ thị hàm số
Tìm các điểm đặc biệt ( giao điểm của đồ thị với hai trục tọa độ , điểm uốn hoặc các điểm khác )
Biểu diễn các điểm cực trị và các điểm đặc biệt lên hệ trục tọa độ Oxy , dựa vào chiều mũi tên trong bảng biến thiên để vẽ đồ thị của hàm số
 CHÚ Ý : Hàm số bậc ba có hai cực trị hoặc không có cực trị
a > 0
a < 0
Pt y’ = 0 có hai nghiệm phân biệt.
Pt y’ = 0 có nghiệm kép
Pt y’ = 0 vô nghiệm
 II. Các dạng toán liên quan thường gặp 
Hàm số đồng biến (hoặc nghịch biến) trên R
Miền xác định : D = R
Tính đạo hàm 
Hàm số đồng biến trên R 
 2. Hàm số có cực đại và cực tiểu
Miền xác định : D = R
Tính đạo hàm 
Hàm số có cực đại và cực tiểu có hai nghiệm phân biệt
	3. Hàm số đạt cực trị tại 
Miền xác định : D = R
Tính đạo hàm 
Hàm số đạt cực trị tại khi : 
4 . Dùng đồ thị biện luận theo m số nghiệm của phương trình
	Các bước thực hiện :
 Giả sử biện luận theo m số nghiệm của phương trình 
Biến đổi phương trình đã cho thành : (1)
 (1) là phương trình hoành độ giao điểm của (C) và đường thẳng . Do đó số giao điểm của chúng chính là số nghiệm của phương trình (1)
Dựa vào đồ thị (C) ta biện luận theo 5 trường hợp sau :
+ < giá trị cực tiểu : phương trình có 1 nghiệm
+ = giá trị cực tiểu : Phương trình có 2 nghiệm
+ Giá trị cực tiểu < < giá trị cực đại : Phương trình có 3 nghiệm
+ = giá trị cực đại : Phương trình có 2 nghiệm
+ > giá trị cực đại : Phương trình có 1 nghiệm
Số giao điểm của đồ thị hàm số và đường thẳng d : 
Lập phương trình hoành độ giao điểm của (C) và d : (2)
Biến đổi (2) thành dạng phương trình tích số , giả sử (2) có nghiệm là ta có 
Tùy theo yêu cầu của bài toán , ta lập luận liên quan đến số nghiệm của (2) , dẫn đến điều kiện về nghiệm của (3)
	6. Phương trình tiếp tuyến của đồ thị hàm số
	 a. Viết phương trình tiếp tuyến của đồ thị (C) tại điểm 
Tính đạo hàm 
Tính 
Áp dụng công thức : 
Chú ý : Nếu đề bài chỉ cho ta phải tìm 
 Nếu đề bài cho , ta phải tìm bằng cách giải phương trình
 b. Viết phương trình tiếp tuyến của đồ thị (C) khi biết hệ số góc của tiếp tuyến bằng k
Tính đạo hàm 
Gọi là tiếp điểm. Ta có : 
Giải phương trình trên tìm , suy ra 
Áp dụng công thức : 
Chú ý : Đôi lúc đề bài không cho trực tiếp giá trị k mà gián tiếp cho nó thông qua quan hệ giữa hai đường thẳng là song song nhau hoặc vuông góc nhau. Khi đó ta phải đi tìm k bằng các điều kiện sau :
 Giả sử có hai đường thẳng và 
Bài tập rèn luyện :
Bài 1 : Viết phương trình tiếp tuyến của đồ thị (C) của hàm số:
	1. tại điểm trên (C) có hoành độ bằng 2
	2. tại điểm trên (C) có tung độ bằng 8
	3. tại giao điểm của (C) với trục tung
Bài 2 : Viết phương trình tiếp tuyến của đồ thị (C) của hàm số
	1. biết tiếp tuyến có hệ số góc bằng 9
	2. biết tiếp tuyến song song với đường thẳng 
	3. biết tiếp tuyến vuông góc với đường thẳng 
Bài 3 : Tìm m để hàm số:
	1. có cực đại và cực tiểu
	2. có cực đại và cực tiểu
	3. đạt cực đại tại 
Bài 4 : Tìm m để hàm số :
	1. đồng biến trên R
	2. nghịch biến trên R
Bài 5 : Chứng minh rằng hàm số sau luôn có cực đại và cực tiểu : 
Bài 6 : Khảo sát sự biến thiên và vẽ đồ thị (C) của các hàm số :
	1. 2. 	3. 
	4. 5. 6. 
Bài 7 : Cho hàm số có đồ thị là (C)
Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Biện luận theo k số nghiệm của phương trình : 
Viết phương trình tiếp tuyến của (C) tại điểm , biết 
Bài 8 : Cho hàm số có đồ thị là (C)
Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng 3
Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc bằng 24
Bài 9 : Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Tìm các giá trị của tham số m để phương trình có ba nghiệm phân biệt
Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ 
Bài 10 : Cho hàm số , có đồ thị (C)
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
Tìm tọa độ giao điểm của (C) với đường thẳng d: 
Dùng đồ thị (C) biện luận theo m số nghiệm phương trình : 
Bài 11 : Cho hàm số , có đồ thị (C)
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có tung độ y = -2
Tìm m để đường thẳng d : cắt đồ thị (C) tại 3 điểm phân biệt
Bài 12 : Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 1
Tìm m để hàm số đạt cực trị tại 
B. Hàm số trùng phương 
I. Sơ đồ khảo sát hàm số
	+ Tập xác định hàm số
	+ Chiều biến thiên
Tính đạo hàm 
Giải phương trình 
Tính giới hạn hàm số khi 
Lập bảng biến thiên
Kết luận các khoảng đồng biến , nghịch biến của hàm số, cực trị của hàm số
+ Vẽ đồ thị hàm số
Tìm các điểm đặc biệt ( giao điểm của đồ thị với hai trục tọa độ , các điểm khác )
Biểu diễn các điểm cực trị và các điểm đặc biệt lên hệ trục tọa độ Oxy , dựa vào chiều mũi tên trong bảng biến thiên để vẽ đồ thị của hàm số
 CHÚ Ý : Hàm số trùng phương : có 1 cực trị khi a và b cùng dấu hoặc b = 0, có 3 cực trị khi a và b trái dấu
Hàm số y = ax4 + bx2 + c (a 
a > 0
a < 0
Pt y’ = 0 có ba nghiệm phân biệt
Pt y’ = 0 có một nghiệm
II. Các dạng toán thường gặp giống như hàm số bậc ba
III. Bài tập rèn luyện :
	Bài 1 : Cho hàm số có đồ thị là (C)
Khảo sát sự biến thiên và vẽ đồ thị (C) của đồ thị hàm số
Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ 
Biện luận theo m số nghiệm của phương trình : 
Bài 2 : Cho hàm số : có đồ thị là (C)
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số 
Biện luận theo m số nghiệm của phương trình : 
Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc bằng 24
Bài 3 : Cho hàm số có đồ thị là (C)
Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Dựa vào đồ thị (C), xác định m để phương trình : có 4 nghiệm phân biệt
Bài 4 : Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với oy
Bài 5 : Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
Viết phương trình tiếp tuyến của (C), biết tiếp tuyến vuông góc với đường thẳng 
Bài 6 : Cho hàm số có đồ thị (C)
Khảo sát sự biến thiên và vẽ dồ thị (C) của hàm số
Tìm m để phương trình sau có 4 nghiệm phân biệt : 
Bài 7 : Cho hàm số (1)
Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 0
Tìm m để đường thẳng y = -1 cắt đồ thị của hàm số (1) tại 4 điểm phân biệt 
C. HÀM NHẤT BIẾN
I. Sơ đồ khảo sát hàm số
	+ Tập xác định hàm số
	+ Chiều biến thiên
Tính đạo hàm 
Tìm tiệm cận của đồ thị hàm số
Lập bảng biến thiên
Kết luận các khoảng đồng biến , nghịch biến của hàm số
+ Vẽ đồ thị hàm số
Tìm các điểm đặc biệt ( giao điểm của đồ thị với hai trục tọa độ , các điểm khác )
Biểu diễn các điểm đặc biệt lên hệ trục tọa độ Oxy , dựa vào chiều mũi tên trong bảng biến thiên để vẽ đồ thị của hàm số
CHÚ Ý : Hàm số nhất biến không có cực trị , đồ thị luôn có đường tiệm cận đứng và tiệm cận ngang và nhận giao điểm của hai đường tiệm cận làm tâm đối xứng
Hàm số y = 
D = ad – bc > 0
D = ad – bc < 0
Bài 1. Cho hàm số (C)
Khào sát và vẽ đồ thị (C) của hàm số .
Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ .
Viết phương trình tiếp tuyến của (C) tại điểm có tung độ .
Viết phương trình tiếp tuyến của (C) , biết hệ số góc của tiếp tuyến .
Tìm m để đường thẳng cắt (C) tại 2 điểm phân biệt .
Bài 2. Cho hàm số (C)
Khào sát và vẽ đồ thị (C) của hàm số .
Viết phương trình tiếp tuyến của (C) tại điểm có tung độ .
Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến song song với đường
 thẳng .
Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến vuông góc với đường thẳng .
Tìm m để đường thẳng cắt đồ thị (C) tại 2 điểm phân biệt có hoành độ âm .
Bài 3. Cho hàm số (C)
Khào sát và vẽ đồ thị (C) của hàm số .
Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) và trục hoành .
Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) và trục tung .
Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến vuông góc với đường thẳng .
Tìm m để đường thẳng cắt đồ thị (C) tại 2 điểm phân biệt có hoành độ dương .
Bài 4. Cho hàm số (C)
Khào sát và vẽ đồ thị (C) của hàm số .
Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến song song với đường phân giác của góc phần tư thứ nhất .
Tìm m để đường thẳng cắt đồ thị (C) tại hai điểm A, B phân biệt .Tìm tập hợp trung điểm I của đoạn thẳng AB .
Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến vuông góc với đường thẳng .
Tìm những điểm trên đồ thị (C) có toạ độ với hoành độ và tung độ đều là số nguyên .
Bài 5. Cho hàm số (C)
Khào sát và vẽ đồ thị (C) của hàm số .
Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến vuông góc với đường phân giác của góc phần tư thứ hai .
Viết phương trình đường thẳng qua điểm và tiếp xúc với đồ thị (C) .
Tìm m để đường thẳng đồ thị (C) tại hai điểm A, B phân biệt .Tìm tập hợp trung điểm I của đoạn thẳng AB .
Tìm những điểm trên đồ thị (C) có toạ độ với hoành độ và tung độ đều là số nguyên .
Bài 6. Cho hàm số (C)
Khào sát và vẽ đồ thị (C) của hàm số .
Viết phương trình tiếp tuyến của đồ thị (C) , biết tiếp tuyến song song với đường phân giác của góc phần tư thứ hai .
Viết phương trình đường thẳng qua điểm và tiếp xúc với đồ thị (C) .
Tìm những điểm trên đồ thị (C) có toạ độ với hoành độ và tung độ đều là số nguyên .
Chứng minh rằng tích các khoảng cách từ một điểm bất kỳ trên (C) đến hai đường tiệm cận của (C) là một hằng số .
Bài 7. Cho hàm số (C)
Khào sát và vẽ đồ thị (C) của hàm số .
Tìm m để đường thẳng cắt đồ thị (C) tại hai điểm phân biệt A, B 
Chứng minh rằng tích các khoảng cách từ một điểm bất kỳ trên (C) đến hai đường tiệm cận của (C) là một hằng số .
Bài 8. Cho hàm số (C)
Khào sát và vẽ đồ thị (C) của hàm số .
Viết phương trình tiếp tuyến của (C) tại các giao điểm của (C) và đường thẳng .
.
Bài 9. Cho hàm số (C)
Khảo sát và vẽ đồ thị (C) của hàm số .
Tìm những điểm trên (C) sao cho khoảng từ điểm đó đến trục hoành gấp đôi khoảng cách từ đó đến trục tung .
Viết phương trình tiếp tuyến của (C) tại những điểm tìm được ở câu 2 .