Chuyên đề Khảo sát hàm số lớp 12

Chuyeân ñeà 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ 
Trong bài này chúng ta sẽ ứng dụng đạo hàm để xét tính đơn điệu (tức là tính đồng biến và nghịch biến) của 
hàm số. Đồng thời sẽ xét các ứng dụng của tính đơn điệu trong việc chứng minh bất đẳng thức, giải phương 
trình, bất phương trình và hệ phương trình. 
A. TÓM TẮT GIÁO KHOA 
Giả sử K là một khoảng, một đoạn hoặc một nữa khoảng và f là hàm số xác định trên K. 
I) ĐỊNH NGHĨA 
 Hàm số f được gọi là đồng biến (tăng) trên K nếu 
    1 2 1 2 1 2x , x K, x x f x f x     
 Hàm số f được gọi là nghịch biến (giảm) trên K nếu 
    1 2 1 2 1 2x , x K, x x f x f x     
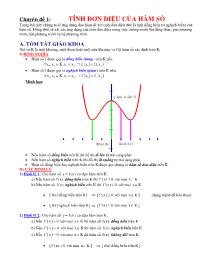
Minh họa: 
-2.5 -2 -1.5 -1 -0.5 0.5 1 1.5 2
-0.5
0.5
1
1.5
2
2.5
x
y
K=(-1;0) K=(1/2;1)
y=f(x)=x4-2x2+2
  Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải 
 Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải 
 Hàm số đồng biến hay nghịch biến trên K được gọi chung là hàm số đơn điệu trên K. 
II) CÁC ĐỊNH LÝ 
1) Định lý 1: Cho hàm số y f (x) có đạo hàm trên K. 
 a) Nếu hàm số f (x) đồng biến trên K thì f '(x) 0 với mọi x K 
 b) Nếu hàm số f (x) nghịch biến trên K thì f '(x) 0 với mọi x K 
 [ f(x) đồng biến trên K]  [ f '(x) 0 với mọi x K ] (dạng mệnh đề kéo theo) 
 [ f(x) nghịch biến trên K]  [ f '(x) 0 với mọi x K ] 
2) Định lý 2: Cho hàm số y f (x) có đạo hàm trên K. 
 a) Nếu  f ' x 0 với mọi x K thì hàm số f (x) đồng biến trên K 
 b) Nếu  f ' x 0 với mọi x K thì hàm số f (x) nghịch biến trên K 
 c) Nếu  f ' x 0 với mọi x K thì hàm số f (x) không đổi trên K 
 [ f '(x) 0 với mọi x K ]  [ f(x) đồng biến trên K] 
 [ f '(x) 0 với mọi x K ]  [ f(x) nghịch biến trên K] 
 [ f '(x) 0 với mọi x K ]  [ f(x) không đổi trên K] 
Chú ý quan trọng: 
Khoảng K trong định lý trên có thể được thay bởi một đoạn hoặc một nữa khoảng. Khi đó phải bổ sung giả 
thiết 
"Hàm số liên tục trên đoạn hoặc nữa khoảng đó". Cụ thể 
 Nếu hàm số liên tục trên đọan  a;b và có đạo hàm f '(x) 0 trên khoảng  a;b thì hàm số f đồng 
biến trên đọan  a;b 
 Nếu hàm số liên tục trên đọan  a;b và có đạo hàm f '(x) 0 trên khoảng  a;b thì hàm số f nghịch 
biến trên đọan  a;b 
3) Định lý 3: (Định lý mở rộng) Cho hàm số y f (x) có đạo hàm trên K. 
 a) Nếu  f ' x 0 với mọi x K và  f ' x 0 chỉ tại một số điểm hữu hạn thuộc K 
 thì hàm số f (x) đồng biến trên K. 
 b) Nếu  f ' x 0 với mọi x K và  f ' x 0 chỉ tại một số điểm hữu hạn thuộc K 
 thì hàm số f (x) nghịch biến trên K. 
Tính đơn điệu của hàm số bậc ba 
4) Định lý 4: Cho hàm số bậc ba    3 2y f x ax bx cx d a 0      , ta có   2f ' x 3ax 2bx c   . 
a) Hàm số    3 2y f x ax bx cx d a 0      đồng biến trên     2f ' x 3ax 2bx c 0 x      
b) Hàm số    3 2y f x ax bx cx d a 0      nghịch biến trên     2f ' x 3ax 2bx c 0 x      
B. THỰC HÀNH GIẢI TOÁN 
I. CÁC DẠNG TOÁN CƠ BẢN 
1.Dạng 1: Xét chiều biến thiên của hàm số. 
Ví dụ 1: Tìm các khoảng đơn điệu của các hàm số sau 
   
   
   
3 2 3 2
4
2 4 2
2
a) y f x x x x 3 b) y f x x 3x 9x 11
xc) y f x 2x 6 d) y f x x 4x 3
4
3x 1 x 2x 2e) y f x f ) y f x
x 1 x 1
          
        
      
Ví dụ 2: Xét chiều biến thiên của các hàm số sau 
2a) y x 2 x b) y x 4 x
2x 3 xc) y d) y
2 2x 1 x 1
    
 
 
2.Dạng 2: Định tham số để hàm số đơn điệu trên một miền K cho trước. 
Ví dụ 1: Tìm các giá trị của tham số m để hàm số 
 a)    3 21y x mx m 6 x 2m 1
3
      đồng biến trên  
 b)    3 21y x m 1 x m 3 x 4
3
       nghịch biến trên  
Ví dụ 2: Tìm các giá trị của tham số m sao cho hàm số      3 2 2f x x m 1 x 2m 1 x m 2       
 a) Đồng biến trên  
 b) Đồng biến trên nữa khoảng 3 ;
2
   
Ví dụ 3: Tìm các giá trị của tham số a sao cho hàm số    3 2 21 1f x x ax 2a 3a 1 x 3a3 2       
 a) Nghịch biến trên  
 b) Nghịch biến trên mỗi nữa khoảng  ; 1  và  3; 
II. CÁC DẠNG TOÁN NÂNG CAO 
1.Dạng 1: Sử dụng tính đơn điệu chứng minh bất đẳng thức. 
 a) Ví dụ 1: Chứng minh các bất đẳng thức sau: 
 i) sin x x với mọi x 0;
2
    
 ii) 
2xcos x 1
2
  với mọi x 0;
2
    
 b) Ví dụ 2: Chứng minh các bất đẳng thức sau: 
 i) 2sin x tan x 3x  với mọi x 0;
2
    
 ii) sin x tan x 2x  với mọi x 0;
2
    
2.Dạng 2: Sử dụng tính đơn điệu giải phương trình, hệ phương trình, bất phương trình. 
 Bổ sung các tính chất của tính đơn điệu 
 Tính chất 1: Giả hàm số  y f x đồng biến (nghịch biến) trên khoảng  a;b và  u; v a;b ta có: 
    f u f v u v    
 Tính chất 2: Giả hàm số  y f x đồng biến trên khoảng  a;b và  u; v a;b ta có: 
    f u f v u v    
 Tính chất 3: Giả hàm số  y f x nghịch biến trên khoảng  a;b và  u; v a;b ta có: 
    f u f v u v    
 Tính chất 4: Nếu hàm số  y f x đồng biến trên  a;b và  y g x làm hàm hằng hoặc là một 
hàm số nghịch biến trên  a;b thì phương trình    f x g x có nhiều nhất một nghiệm thuộc 
khoảng  a;b 
 Dựa vào tính chất trên ta suy ra: 
 Nếu có  0x a;b sao cho    0 0f x g x thì phương trình    f x g x có nghiệm duy nhất trên 
 a;b 
 a) Ví dụ 1: Giải phương trình x 9 2x 4 5    
 b) Ví dụ 2: Giải phương trình 2x cos x 0
4 2
    
 c) Ví dụ 3: Giải phương trình 2 2x 15 3x 2 x 8     
 d) Ví dụ 4: Giải bất phương trình x 2 3 x 5 2x     
 e) Ví dụ 5: Giải hệ phương trình cot x cot y x y5x 8y 2     với  x, y 0;  
 f) Ví dụ 6: Giải hệ phương trình: x y 1 y 1 x 0
x 1 y 2
         
C. BÀI TẬP VỀ NHÀ 
Bài 1: Tìm các khoảng đơn điệu của các hàm số sau 
   
   
3 2 4 2
2
a) y f x x 3x 9x 5 b) y f x x 2x 3
2x 1 x 2x 3c) y f x d) y f x
x 1 x 2
          
      
Bài 2: Lập bảng biến thiên của các hàm số sau 
  
2a) y x 4 x
b) y x 1 9 x
c) y x 1 8 x x 1 8 x
  
   
      
Bài 3: Cho hàm số    3 21y a 1 x ax 3a 2 x 2
3
      
 Tìm a để hàm số đồng biến trên  
Bài 4: Tùy theo m hãy xét sự biến thiên của hàm số  2y x m x m   
Bài 5: Giải các phương trình sau: 
2
3
a) 4x 1 4x 1 1
b) sin x cos x 2x 1 0
c) 4x 12x 8 cos3x 9cos x 0
   
   
    
Bài 6: Giải bất phương trình 2x x 6 x 2 18    
Bài 7: Giải hệ phương trình 
3 2
3 2
3 2
2x 1 y y y
2y 1 z z z
2z 1 x x x
            
Bài 8: Cho tam giác ABC có ba góc nhọn. Chứng minh rằng: 
 sin A sin B sin C tan A tan B tan C 2       
------------------------Hết----------------------- 
Chuyên đề 3: GIÁ TRỊ LỚN NHẤT 
 VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ 
A. TÓM TẮT GIÁO KHOA 
I) ĐỊNH NGHĨA: Giả sử hàm số  y f x xác định trên tập hợp D. 
 Số M được gọi là GTLN của hàm số  y f x trên tập D nếu các điều sau được thỏa mãn 
    0 0
i) f x M x D
ii) x D : f x M
       
 Ký hiệu: 
 Số m được gọi là GTNN của hàm số  y f x trên tập D nếu các điều sau được thỏa mãn 
    0 0
i) f x m x D
ii) x D : f x m
       
 Ký hiệu:  
x D
m min f x

 
Minh họa: 
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
x
y
y=f(x)=x3-3x+4
-5/2 3/2
m=33/8
M=6
D=[-5/2;3/2]
  Quy ước: Ta quy ước rằng khi nói GTLN hay GTNN của hàm số f mà không nói "trên tập D" thì ta 
hiểu đó là GTLN hay GTNN trên TẬP XÁC ĐỊNH của nó. 
 Đối với GTLN và GTNN đối với hàm nhiều biến cũng có định nghĩa tương tự. 
II) CÁC PHƯƠNG PHÁP THƯỜNG DÙNG ĐỂ TÌM GTLN & GTNN CỦA HÀM SỐ MỘT BIẾN: 
1) Phương pháp 1 : Sử dụng bất đẳng thức (hay phương pháp dùng định nghĩa). 
 Một số kiến thức thường dùng: 
 a) 2 2( ) ( )
2 4
bf x ax bx c a x
a a
      
 b) Bất đẳng thức Cô-si: Với hai số a, b không âm  a, b 0 ta luôn có: a b ab
2
  
 Dấu "=" xảy ra khi a b 
2) Phương pháp 2 : Sử dụng điều kiện có nghiệm của phương trình (hay phương pháp miền giá trị). 
 Một số kiến thức thường dùng: 
 a) Phương trình  2ax bx c 0 a 0    có nghiệm 0   
 b) Phương trình  a cos x bsin x c a, b 0   có nghiệm 2 2 2a b c   
 Cơ sở lý thuyết của phương pháp: Cho hàm số xác định bởi biểu thức dạng  y f x 
 Tập xác định của hàm số được định nghĩa là : D  { x | f(x) có nghĩa} 
 Tập giá trị của hàm số được định nghĩa là : T = { y | Phương trình f(x) = y có nghiệm x D } 
 Do đó nếu ta tìm được tập giá trị T của hàm số thì ta có thể tìm đựơc GTLN và GTNN của hàm số 
đó. 
3) Phương pháp 3 : Sử dụng đạo hàm (hay phương pháp giải tích). 
 Điều kiện tồn tại GTLN và GTNN: 
 Định lý: Hàm số liên tục trên một đoạn  a;b thì đạt được GTLN và GTNN trên đoạn đó. 
 (Weierstrass 2) 
 Phương pháp chung: Muốn tìm GTLN và GTNN của hàm số  y f x trên miền D, ta lập 
BẢNG BIẾN THIÊN của hàm số trên D rồi dựa vào BBT suy ra kết quả. 
 Phương pháp riêng: 
  Chú ý: Phải kiểm tra tính liên tục của hàm số  y f x trên đoạn  a;b , tránh áp dụng một cách hình 
thức. 
B. THỰC HÀNH GIẢI TOÁN 
1) Phương pháp 1 : Sử dụng bất đẳng thức 
 Ví dụ 1: Tìm GTLN của hàm số   2f x 2x 8x 1    
 Ví dụ 2: Tìm GTNN của hàm số   2 f x 2x 4x 12    
 Ví dụ 3: Tìm GTNN của các hàm số sau 
 a)   2f x x
x 1
   với  x 1;  
 b) 7f (x) x 3
x 3
    
2) Phương pháp 2 : Sử dụng điều kiện có nghiệm của phương trình 
 Ví dụ 1 : Tìm GTLN và GTNN của hàm số 
2
2
x x 2y
x x 2
    
 Ví dụ 2: Tìm GTLN và GTNN của hàm số 1 sin xy
2 cos x
  
3) Phương pháp 3 : Sử dụng đạo hàm 
 Ví dụ 1: Tìm GTLN và GTNN của các hàm số sau: 
 3 2a) y x 3x 9x 35    trên đoạn  4, 4 x 2b) y
x 2
  trên đoạn  0;2 
 c) y s in2x x  trên đoạn ;
2 2
     
2d) y x 2 x   
 e) 2025 2011y x  trên đoạn  0;1 f) 2
1
xy
x
  trên đoạn  0;1 
 g) 
2 3 6
1
x xy
x
    trên đoạn  2;6 h) 2xy x e  trên đoạn  1;0 
 Ví dụ 2: Tìm GTLN và GTNN của hàm số 
 a) 34y 2sin x sin x
3
  trên đoạn  0; b) 4 2y cos x 6cos x 5   
Chuyeân ñeà 4: CUNG LỒI - CUNG LÕM VÀ ĐIỂM UỐN 
TÓM TẮT GIÁO KHOA 
1. Khái nhiệm về cung lồi, cung lõm và diểm uốn 
 Tại mọi điểm của cung AC , tiếp tuyến luôn luôn ở phía trên của AC . Ta nói AC là một cung lồi. 
 Tại mọi điểm của cung CB, tiếp tuyến luôn luôn ở phía dưới của CB. Ta nói CB là một cung lõm. 
 Điểm C phân cách giữa cung lồi và cung lõm được gọi là điểm uốn của đồ thị. Tại điểm uốn tiếp 
tuyến đi xuyên qua đồ thị. 
2. Dấu hiệu nhận biết lồi, lõm và điểm uốn 
Định lý 1: Cho hàm số y f (x) có đạo hàm cấp hai trên khoảng  a;b . 
 Nếu f ''(x) 0 với mọi  x a;b thì đồ thị của hàm số lồi trên khoảng đó. 
 Nếu f ''(x) 0 với mọi  x a;b thì đồ thị của hàm số lõm trên khoảng đó. 
Định lý 2: Cho hàm số y f (x) có đạo hàm cấp hai trên khoảng  a;b và  0x a;b 
 Nếu f "(x) đổi dấu khi x đi qua x0 thì điểm  0 0 0M x ;f (x ) là điểm uốn của đồ thị hàm số đã cho. 
3. Áp dụng 
 Ví dụ: Tìm khoảng lồi lõm và điểm uốn của đồ thị các hàm số ...  (C) bieát tieáp tuyeán song song vôùi ñöôøng thaúng (d): y = 4x+2. 
Ví duï 2: Cho ñöôøng cong (C): 
1
32


x
xy 
 Vieát phöông trình tieáp tuyeán vôùi (C) bieát tieáp tuyeán vuoâng goùc vôùi ñöôøng thaúng xy 3:)(  
(C): y=f(x) 

x
y
ak /1
O
baxy  :2
(C): y=f(x) 
x
y
ak 
baxy 
1
2
c. Daïng 3: 
 Vieát phöông trình tieáp tuyeán vôùi (C): y=f(x) bieát tieáp tuyeán ñi qua ñieåm A(xA;yA) 
Phöông phaùp 1 : Ta coù theå tieán haønh theo caùc böôùc sau 
Böôùc 1: Vieát phöông trình ñöôøng thaúng ( ) qua A vaø coù heä soá 
 goùc laø k bôûi coâng thöùc: 
 ( ) ( )A A A Ay y k x x y k x x y       (*) 
 Böôùc 2: Ñònh k ñeå ( ) tieáp xuùc vôùi (C). Ta coù: 
 A'
f(x)=k(x-x )
 tieáp xuùc (C) heä coù nghieäm (1)
f ( )
Ay
x k
   
 Böôùc 3: Giaûi heä (1) tìm k. Thay k tìm ñöôïc vaøo (*) ta seõ ñöôïc pttt caàn tìm. 
Phöông phaùp 2 : Ta coù theå tieán haønh theo caùc böôùc sau 
 0 0M(x ,y ) 
  
 Böôùc 1: Gọi 0 0M(x ;y ) là một điểm tùy ý trên (C) với 0 0y f(x ) 
 Phương trình tiếp tuyến với (C) tại M có dạng 
 0 0 0( ) : y f '(x )(x x ) f(x )    (1) 
 Böôùc 2: Tìm x0 để ( ) đi qua A AA(x ;y ) 
 A A 0 0A 0AA(x ;y ) ( ) f '(x )( x ) f(y x ) ( )x 2      
 Giải phương trình (2) tìm x0 
 Böôùc 3: Thay x0 vào phương trình (1) ta được pttt cần tìm. 
x
y
AAAA yxxkyxxkyy  )()(:
O
);( AA yxA
)(:)( xfyC 
x
y
0 0 0: y f '(x )(x x ) f(x )   
O
);( AA yxA
)(:)( xfyC 
AÙp duïng: 
Ví duï1: Cho ñöôøng cong (C): 43 23  xxy 
 Vieát phöông trình tieáp tuyeán vôùi (C) bieát tieáp tuyeán ñi qua ñieåm A(0;-1) 
Ví duï 2: Cho ñöôøng cong (C): 2 5
2
xy
x
  
 Vieát phöông trình tieáp tuyeán vôùi (C) bieát tieáp tuyeán ñi qua ñieåm A(-2;0). 
BAØI TAÄP REØN LUYEÄN 
Baøi 1: Cho ñöôøng cong (C): 
2
12


x
xxy 
 Vieát phöông trình tieáp tuyeán vôùi (C) bieát tieáp tuyeán vuoâng goùc vôùi ñöôøng thaúng 2:)(  xy 
Baøi 2: Cho haøm soá 
1
632


x
xxy (C) 
 Tìm treân ñoà thò (C) caùc ñieåm maø tieáp tuyeán taïi ñoù vuoâng goùc vôùi ñöôøng thaúng xyd
3
1:)(  
Baøi 3: Cho ñöôøng cong (C): 
2 1
1
x xy
x
   
 Tìm caùc ñieåm treân (C) maø tieáp tuyeán vôùi (C) taïi ñoù vuoâng goùc vôùi tieäm caän xieân cuûa (C). 
Baøi 4: Cho haøm soá 
3
1
23
1 23  xmxy (Cm) 
 Goïi M laø ñieåm thuoäc (Cm) coù hoaønh ñoä baèng -1 . Tìm m ñeå tieáp tuyeán cuûa (Cm) taïi ñieåm M song 
 song vôùi ñöôøng thaúng 5x-y=0 
Baøi 5: Cho ñöôøng cong (C): 23 23  xxy 
 Vieát phöông trình tieáp tuyeán vôùi (C) bieát tieáp tuyeán ñi qua ñieåm M(2;-7) 
RÈN LUYỆN GIẢI ĐỀ TUYỂN SINH 
Baøi 1: 
Bài 2: 
Bài 3: 
Bài 4: 
Bài 5: 
4.BAØI TOAÙN 4: BIEÄN LUAÄN SOÁ NGHIEÄM CUÛA PHÖÔNG TRÌNH BAÈNG ÑOÀ THÒ 
Cô sôû cuûa phöông phaùp: 
 Xeùt phöông trình f(x) = g(x) (1) 
 Nghieäm x0 cuûa phöông trình (1) chính laø hoaønh ñoä giao ñieåm cuûa (C1):y=f(x) vaø (C2):y=g(x) 
Daïng 1 : Baèng ñoà thò haõy bieän luaän theo m soá nghieäm cuûa phöông trình : f(x) = m (*) 
 Phöông phaùp: 
 Böôùc 1: Xem (*) laø phöông trình hoaønh ñoä giao ñieåm cuûa hai ñoà thò: 
 
   
 ( ) : ( ) : (C) laø ñoà thi coá ñinh
 ( ) : : ( ) laø ñöôøng thaúng di ñoäng cuøng phöông Ox 
 vaø caét Oy taïi M(0;m)
C y f x
y m 
 Böôùc 2: Veõ (C) vaø ( ) leân cuøng moät heä truïc toïa ñoä 
 Böôùc 3: Bieän luaän theo m soá giao ñieåm cuûa ( ) vaø (C) 
 Töø ñoù suy ra soá nghieäm cuûa phöông trình (*) 
 Minh hoïa: 
y
x
)(:)( xfyC 
);0( m
1m
2m
my 
O
y
x
0x
)( 1C
)( 2C
Daïng 2: Baèng ñoà thò haõy bieän luaän theo m soá nghieäm cuûa phöông trình : f(x) = g(m) (* *) 
Phöông phaùp: Ñaët k=g(m) 
 Böôùc 1: Xem (**) laø phöông trình hoaønh ñoä giao ñieåm cuûa hai ñoà thò: 
 
   
 ( ) : ( ) : (C) laø ñoà thi coá ñinh
 ( ) : : ( ) laø ñöôøng thaúng di ñoäng cuøng phöông Ox 
 vaø caét Oy taïi M(0;k)
C y f x
y k 
 Böôùc 2: Veõ (C) vaø ( ) leân cuøng moät heä truïc toïa ñoä 
 Böôùc 3: Bieän luaän theo k soá giao ñieåm cuûa ( ) vaø (C) . Döï a vaøo heä thöùc k=g(m) ñeå suy ra m 
 Töø ñoù keát luaän veà soá nghieäm cuûa phöông trình (**). 
Minh hoïa: 
AÙp duïng: 
Ví duï: 1) Khaûo saùt söï bieán thieân vaø veõ ñoà thò haøm soá 41292 23  xxxy 
 2) Bieän luaän theo m soá nghieäm cuûa phöông trình: 041292 23  mxxx 
 3) Tìm m ñeå phöông trình sau coù 6 nghieäm phaân bieät: mxxx  1292 23 
BAØI TAÄP REØN LUYEÄN 
Baøi 1: Bieän luaän theo m soá nghieäm cuûa caùc phöông trình : 
 a.
2
1
x m
x
 b. 
2
1
x m
x
 
Baøi 2: Tìm k ñeå phöông trình sau coù ba nghieäm phaân bieät: 
 3 2 3 23 3 0x x k k     
Baøi 3: Tìm m ñeå phöông trình sau coù nghieäm duy nhaát: 
 3 3 2 0x mx   
Baøi 4 :Tìm m ñeå phöông trình sau coù hai nghieäm phaân bieät: 
 22 4 3 2 1 0x x m x     
x
y
 ky 
);0( k
K
1M
O
2K
RÈN LUYỆN GIẢI ĐỀ TUYỂN SINH 
Bài 1: 
Bài 2: 
5. BAØI TOAÙN 5: HOÏ ÑÖÔØNG CONG 
BAØI TOAÙN TOÅNG QUAÙT: 
Cho hoï ñöôøng cong ),(:)( mxfyCm  ( m laø tham soá ) 
Bieän luaän theo m soá ñöôøng cong cuûa hoï )( mC ñi qua ñieåm );( 000 yxM cho tröôùc. 
PHÖÔNG PHAÙP GIAÛI: 
Ta coù : 
 Hoï ñöôøng cong )( mC ñi qua ñieåm );( 000 yxM  ),( 00 mxfy  (1) 
Xem (1) laø phöông trình theo aån m. 
Tuøy theo soá nghieäm cuûa phöông trình (1) ta suy ra soá ñöôøng cong cuûa hoï (Cm) ñi qua M0 
Cuï theå: 
 Neáu phöông trình (1) coù n nghieäm phaân bieät thì coù n ñöôøng cong cuûa hoï (Cm) ñi qua M0 
 Neáu phöông trình (1) voâ nghieäm thì moïi ñöôøng cong cuûa hoï (Cm) ñeàu khoâng ñi qua M0 
 Neáu phöông trình (1) nghieäm ñuùng vôùi moïi m thì moïi ñöôøng cong cuûa hoï (Cm) ñeàu ñi qua M0 
 Trong tröôøng hôïp naøy ta noùi raèng M0 laø ñieåm coá ñònh cuûa hoï ñöôøng cong )( mC 
AÙp duïng: 
Ví duï: Goïi (Cm) laø ñoà thò haøm soá mx
mmxy 
2
1 . Tìm m ñeå tieäm caän xieân cuûa (Cm) ñi qua ñieåm 
 A(2;0) 
Ví duï: Cho haøm soá 193 23  xmxxy (1). Tìm m ñeå ñieåm uoán cuûa ñoà thò haøm soá (1) thuoäc ñöôøng 
 thaúng y=x+1 
TÌM ÑIEÅM COÁ ÑÒNH CUÛA HOÏ ÑÖÔØNG CONG 
BAØI TOAÙN TOÅNG QUAÙT: 
Cho hoï ñöôøng cong ),(:)( mxfyCm  ( m laø tham soá ) 
Tìm ñieåm coá ñònh cuûa hoï ñöôøng cong (Cm) 
PHÖÔNG PHAÙP GIAÛI 
Böôùc 1: Goïi );( 000 yxM laø ñieåm coá ñònh (neáu coù) maø hoï (Cm) ñi qua. Khi ñoù phöông trình: 
 ),( 00 mxfy  nghieäm ñuùng m (1) 
Böôùc 2: Bieán ñoåi phöông trình (1) veà moät trong caùc daïng sau: 
 Daïng 1: 0 BAm m 
 Daïng 2: 02  CBmAm m 
 AÙp duïng ñònh lyù: 0 BAm 



0
0
B
A
m (2) 







0
0
0
02
C
B
A
mCBmAm (3) 
 Böôùc 3: Giaûi heä (2) hoaëc (3) ta seõ tìm ñöôïc );( 00 yx 
6. BAØI TOAÙN 6: TÌM CAÙC ÑIEÅM ÑAËC BIEÄT TREÂN ÑOÀ THÒ CUÛA HAØM SOÁ 
Baøi 1: Cho haøm soá 
2 3 6
2
x xy
x
   
 Tìm treân ñoà thò haøm soá taát caû nhöõng ñieåm coù caùc toaï ñoä laø nguyeân . 
Baøi 2: Cho haøm soá 
2 2 2
1
x xy
x
   
 Tìm ñieåm thuoäc ñoà thò haøm soá sao cho khoaûng caùch töø ñoù ñeán truïc hoaønh baèng hai laàn khoaûng 
 caùch töø ñoù ñeán truïc tung . 
Baøi 3: Cho haøm soá 2 1
1
xy
x
  
 Tìm treân ñoà thò haøm soá nhöõng ñieåm coù toång khoaûng caùch ñeán hai tieäm caän nhoû nhaát 
Baøi 4: Cho haøm soá 
2 2 2
1
x xy
x
   
 Tìm ñieåm M treân ñoà thò (C) sao cho khoaûng caùch töø M ñeán giao ñieåm cuûa hai ñöôøng tieäm caän laø 
 nhoû nhaát 
Baøi 5: Cho haøm soá 
2 4 5
2
x xy
x
   
 Tìm ñieåm thuoäc ñoà thò haøm soá sao cho khoaûng caùch töø ñieåm ñoù ñeán ñöôøng thaúng y+3x+6 = 0 laø 
 nhoû nhaát. 
Baøi 6: Cho haøm soá 1
1
y x
x
   (C) 
 Tìm hai ñieåm A,B treân hai nhaùnh khaùc nhau cuûa (C) sao cho ñoä daøi ñoaïn AB nhoû nhaát 
Baøi 7: Cho haøm soá 
2 2
1
x xy
x
   
 Tìm treân ñoà thò haøm soá hai ñieåm ñoái xöùng nhau qua ñieåm 5(0; )
2
I 
Baøi 8: Cho haøm soá 
2
1
xy
x
  
 Tìm treân ñoà thò haøm soá hai ñieåm ñoái xöùng nhau qua ñöôøng thaúng y=x-1 
7. BAØI TOAÙN 7: CAÙC BAØI TOAÙN VEÀ SÖÏ ÑOÁI XÖÙNG 
Baøi 1: Cho haøm soá 
1
12


x
xxy (C). Chöùng minh raèng (C) nhaän giao ñieåm hai tieäm caän ñöùng vaø xieân 
 laøm taâm ñoái xöùng. 
Baøi 2: Cho haøm soá 
2 2 22
1
x m x my
x
   (Cm) 
Tìm taát caû caùc giaù trò cuûa tham soá m ñeå ñoà thò (Cm) coù hai ñieåm phaân bieät ñoái xöùng nhau qua goác 
 toaï ñoä 
Baøi 3: Cho haøm soá 3 2 2 23 3( 1) 1y x mx m x m      (Cm) 
Tìm taát caû caùc giaù trò cuûa tham soá m ñeå ñoà thò (Cm) coù hai ñieåm phaân bieät ñoái xöùng nhau qua goác 
 toïa ñoä 
Baøi 4: Cho haøm soá 
2 4 5
2
x mx my
x
   (Cm) 
Tìm taát caû caùc giaù trò cuûa tham soá m ñeå ñoà thò (Cm) coù hai ñieåm phaân bieät ñoái xöùng nhau qua goác 
 toaïñoä 
----------------------------------Heát----------------------------------- 
BÀI TẬP RÈN LUYỆN 
BÀI TẬP: ĐƠN ĐIỆU – CỰC TRỊ 
 GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT 
Bài 1: (CĐ-2009) 
Kết quả: 5 2
4
m  
Bài 2 (D-2003) 
Kết quả: 
Bài 3: (D-2011) 
Kết quả: 
Bài 4: (B-2002) 
Kết quả: 3m   hoặc 0 3m  
Bài 5: (B-2003) 
Kết quả: 
Bài 6: (B-2005) 
Bài 7: (B-2007) 
Kết quả: 1
2
m   
Bài 8: (B-2011) 
Kết quả: 2 2 2m   
Bài 9: (A-2002) 
Kết quả: 22y x m m   
Bài 10: (A-2005) 
Kết quả: 1m  
Bài 11: (A-2007) 
Kết quả: 4 2 6m    
Bài 12: 
Bài 13: 
Bài 14: 
Bài 15: 
Bài 16: 
Bài 17: 
Bài 18: 
Bài 19: 
Bài 20: 
Bài 21: 
Bài 22: 
Bài 23: 
Bài 24: 
Bài 25: 
Bài 26: 
Bài 27: 
Bài 28: 
-------------------------Hết-------------------------- 
BÀI TẬP: SỰ TƯƠNG GIAO CỦA HAI ĐỒ THỊ 
Bài 1: (CD-2008) 
Kết quả: 0m  hoặc 4m  
Bài 2: (D-2003) 
Kết quả: 1m  
Bài 3: (D-2006) 
Kết quả: 15
4
m  và 24m  
Bài 4: (D-2008) 
Bài 5: (D-2009) 
Kết quả: 1 1
3
m   và 0m  
Bài 6: (D-2009) 
Kết quả: 1m  
Bài 7: (D-2011) 
Kết quả: 3m   
Bài 8: (B-2009) 
Kết quả: 2 6m   
Bài 9: (B-2010) 
Kết quả: 2m   
Bài 10: (A-2003) 
Kết quả: 1 0
2
m   
Bài 11: (A-2004) 
Kết quả: 1 5
2
m  
Bài 12: (A-2010) 
Kết quả: 1 1
4
m   và 0m  
Bài 13: (A-2011) 
Kết quả: 1m   
Bài 14: 
Bài 15: 
Bài 16: 
Bài 17: 
Bài 18: 
Bài 19: 
Bài 20: 
Bài 21: 
Bài 22: 
Bài 23: 
Bài 24: 
Bài 25: 
-------------------------Hết------------------------ 
 BÀI TẬP : TIẾP TUYẾN VỚI ĐỒ THỊ 
Bài 1: (CĐ-2010) 
Bài 2: (CĐ-2011) 
Bài 3: (D-2005) 
Bài 4: (D-2007) 
Bài 5: (D-2010) 
Bài 6: (B-2004) 
Bài 7: (B-2006) 
Bài 8: (B-2008) 
Bài 9: (A-2009) 
Bài 10: (A-2011) 
Bài 11: 
Bài 12: 
Bài 13: 
Bài 14: 
Bài 15: 
Bài 16: 
Bài 17: 
Bài 18: 
Bài 19: 
Bài 20: 
Bài 21: 
Bài 22: 
Bài 23: 
Bài 24: 
Bài 25: 
Bài 26: 
Bài 27: 
Bài 28: 
Bài 29: 
Bài 30: 
Bài 31: 
Bài 32: 
Bài 33: 
Bài 34: 
Bài 35: 
Bài 36: 
Bài 37: 
Bài 38: 
Bài 39: 
Bài 40: 
Bài 41: 
Bài 42: 
Bài 43: 
Bài 44: 
Bài 45: 
Bài 46: 
...................................Hết................................... 
BÀI TẬP: BIỆN LUẬN SỐ NGHIỆM 
 CỦA PHƯƠNG TRÌNH BẰNG ĐỒ THỊ 
Bài 1: (B-2009) 
Bài 2: (A-2002) 
Bài 3: (A-2006) 
Bài 4: 
Bài 5: 
Bài 6: 
Bài 7: 
Bài 8: 
Bài 9: 
Bài 10: 
Bài 11: 
Bài 12: 
------------------------------Hết-----------------------------