Chuyên đề Các phương pháp giải phương trình mũ
Chuyên đề Các Phương Pháp Giải Phương Trình Mũ.
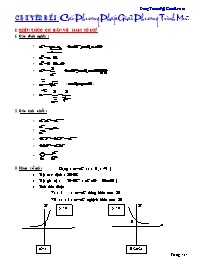
I. KIẾN THỨC CƠ BẢN VỀ HÀM SỐ MŨ
Bạn đang xem tài liệu "Chuyên đề Các phương pháp giải phương trình mũ", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Chuyªn ®Ị I: Các Phương Pháp Giải Phương Trình Mũ. I. KIẾN THỨC CƠ BẢN VỀ HÀM SỐ MŨ 1. Các định nghĩa: ( ) 2. Các tính chất : 3. Hàm số mũ: Dạng : ( a > 0 , a1 ) Tập xác định : Tập giá trị : ( ) Tính đơn điệu: * a > 1 : đồng biến trên * 0 < a < 1 : nghịch biến trên 0<a<1 y=ax a>1 y=ax II. CÁC PHƯƠNG PHÁP GIẢI Phương pháp 1: Đưa về cùng cơ sớ Ví dụ: Giải PT sau: a) b) Bài tập tương tự: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Phương pháp 2: Logarit hóa (lấy logarit 2 vế) Ví dụ 1: Giải PT sau: Lấy logarit cơ sớ 3 hai vế: Chú ý: Có thể logarit theo cơ sớ bất kì cả hai vế. Trong ví dụ trên chọn cơ sớ 3 cho tiện Phương pháp logarit hóa tỏ ra rất hiệu lực khi hai vế phương trình có dạng tích các lũy thừa. Ví dụ 2: Giải PT: Lấy logarit cơ sớ 2 hai vế, ta được: Chú ý: Đới với mợt sớ PT cần thiết rút gọn trước khi logarit hóa. Ví dụ 3: giải PT Biến đởi PT về dạng: Bài tập tương tự: Giải các PT sau 1. 2. 3. Phương pháp 3: Phương pháp đặt ẩn phụ Mục đích của phương pháp này là chuyển các bài toán đã cho về phương trình hoặc bất phương trình đại sớ quen thuợc(chú ý khi đặt ẩn phụ thì phải đi tìm điều kiện cho ẩn phụ) Ví dụ: giải PT: Đặt >0. khi đó PT đã cho có dạng: Với Bài tập tương tự: 1. 2. 3. 4. 5. 6. 7. 8. 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) Phương pháp 4: Đoán nghiệm và chứng minh tính duy nhất nhất nghiệm của PT(phương pháp hàm sớ). Ví dụ 1: Giải PT: Ta thấy x=1 là nghiệm của PT vì , bây giờ ta chứng minh x=1 là nghiệm duy nhất của PT. thật vậy: Với x>1: (vì cơ sơ 4;5 lớn hơn 1) nên x>1 khơng phải là nghiệm của PT Với x<1: nên x<1 khơng phải là nghiệm của PT Vậy x=1 là nghiệm duy nhất của PT trên. Ví dụ 2: Giải PT:(1) Cách 1: + vế trái của PT là mợt hàm đờng biến(vì cơ sớ 3>1) + vế phải của PT là mợt hàm nghịch biến(vì -2<0) + do vậy nếu PT có nghiệm thì nghiệm đó là duy nhất Nhận xét rằng x=1 là nghiệm của PT vì: 31=5-2.1 Vậy x=1 là nghiệm duy nhất của PT Chú ý: Nếu PT có nghiệm , mợt vế của PT là hàm sớ đờng biến, vế kia là hàm sớ nghịch biến(hoặc hàm hằng) thì nghiệm là duy nhất. Bài tập tương tự: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. Bài tập tởng hợp: Bài 1: Hăy giải các pt sau : 1) 2) 3) 4) Bài 2: Hăy giải các pt sau 1) 2) 3) 4) 5) 6) 6) Bài 3: Hăy giải các phương trình sau: 1) 2) 3) 4) 5) Bài 4: Hăy giải các phương trình sau: 1) 2) 3) 4) 5) 6) Bài 5: Hăy giải các phương trình sau: 1) 2) 3) 4) 5) 6)2 7) 8)3.16 9) Bài 6: Giải các phương trình sau: 1) (x=-5) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) ...
Tài liệu đính kèm:
 Chuyen de I cac phuong phap giai phuong trinh mu.doc
Chuyen de I cac phuong phap giai phuong trinh mu.doc





