Chủ đề: Hàm số luỹ thừa, hàm số mũ, hàm số lôgarit
Các dạng toán cần ôn tập
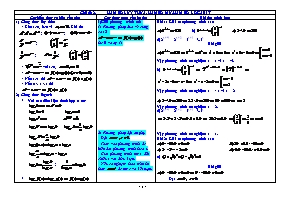
I)Giải phương trình mũ
1) Phương pháp đưa về cùng cơ số:
(a>0 và a≠ 1)
2) Phương pháp đặt ẩn phụ
+Đặt .
+Thay vào phương trình để biến đổi phương trình theo t.
+Giải phương trình tìm t, đối chiếu t với điều kiện.
+Nếu có nghiệm thỏa mãn thì thay để tìm x và kết luận.
Lưu ý:Chọn số chia thích hợp trong pt d) thì sau khi chia ta sẽ được pt đơn giản hơn
Bạn đang xem tài liệu "Chủ đề: Hàm số luỹ thừa, hàm số mũ, hàm số lôgarit", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Chủ đề 2. HÀM SỐ LUỸ THỪA, HÀM SỐ MŨ, HÀM SỐ LÔGARIT Các kiến thức cơ bản cần nhớ Các dạng toán cần ôn tập Bài tập minh hoạ 1) Công thức lũy thừa • Cho a>0, b>0 và . Khi đó ; ; ; ; ; • với a>0, • • Nếu a>1 thì • Nếu 0 < a < 1 thì 2) Công thức lôgarit Với các điều kiện thích hợp ta có: ; (với a>0 và a ≠ 1) Nếu a>1 thì Nếu 0<a<1 thì 3) Đạo hàm của hàm số mũ, hàm số lôgarit Vơí các điều kiện thích hợp ta có ; (logax)' = ; (lnx)' = (logau(x))' = ; (lnu(x))' = (Với u = u(x) ) 4) Phương trình mũ a) Phương trình mũ cơ bản x = logam (0 0) b)Phương pháp giải phương trình mũ * Phương pháp đưa về cùng cơ số: (0<a1) * Phương pháp đặt ẩn phụ + Đặt . + Thay vào phương trình để biến đổi phương trình theo t. + Giải phương trình tìm t, đối chiếu điều kiện. + Nếu có nghiệm thỏa mãn thì thay để tìm x và kết luận. * Phương pháp lôgarit hóa: lấy lôgarit 2 vế đưa phương trình về dạng đơn giản hơn. 5) Phương trình lôgarit a )Phương trình lôgarit cơ bản logax = m x = am (0 0) b)Phương pháp giải phương trình lôgarit * Phương pháp đưa về cùng cơ số * Phương pháp đặt ẩn phụ + Đặt ĐK cho ẩn x (nếu cần) +Đặt . +Thay t vào phương trình và biến đổi phương trình theo t. +Giải phương trình tìm t. +Thay tìm nghiệm x của pt đã cho +Đối chiếu x với ĐK và kết luận c) Phương pháp mũ hóa: mũ hóa hai vế của phương trình với cơ số hợp lí để đưa phương trình về dạng đơn giải hơn. 5) Bất phương trình mũ, bất phương trình lôgarit Cách giải tương tự như cách giải phương trình mũ và lôgarit. I)Giải phương trình mũ 1) Phương pháp đưa về cùng cơ số: (a>0 và a≠ 1) 2) Phương pháp đặt ẩn phụ +Đặt . +Thay vào phương trình để biến đổi phương trình theo t. +Giải phương trình tìm t, đối chiếu t với điều kiện. +Nếu có nghiệm thỏa mãn thì thay để tìm x và kết luận. Lưu ý:Chọn số chia thích hợp trong pt d) thì sau khi chia ta sẽ được pt đơn giản hơn 4) Phương trình lôgarit a) Phương pháp đưa về cùng cơ số Cách 1: +) Đặt ĐK cho pt +)Giải pt f(x) = g(x) để tìm x +)Đối chiếu x với ĐK và kết luận Cách 2 Hoặc Ta chỉ cần giải một trong hai hệ (I) hoặc (II) b) Phương pháp đặt ẩn phụ + Đặt ĐK cho ẩn x (nếu cần) +Đặt . +Thay t vào phương trình và biến đổi phương trình theo t. +Giải phương trình tìm t. +Thay tìm nghiệm x của pt đã cho +Đối chiếu x với ĐK và kết luận Lưu ý : Nếu ẩn x nằm ở cơ số thì phải có đk 0 < x ≠ 1 Lưu ý:Ta chọn một trong hai biểu thức f(x) hoặc g(x) biểu thức nào đơn giản , dễ giải bpt hơn để ghép với pt f(x) = g(x) và giải hệ hỗn hợp se bớt đi được việc giải thêm một bất phương trình 5) Bất phương trình mũ, bất phương trình lôgarit Cách giải tương tự như cách giải phương trình mũ và lôgarit. *Với các điều kiện thích hợp lưu ý cho học sinh nhớ a) Bất phương trình mũ • Nếu a>1 thì • Nếu 0 < a < 1 thì b) Bất phương trình lôgarit Nếu a>1 thì Nếu 0<a<1 thì Lưu ý:Chọn số chia thích hợp trong pt d) thì sau khi chia ta sẽ được pt đơn giản hơn Lưu ý : Nếu sử dụng cách 2 thì việc giải bpt (3) , (4) sẽ ngắn gọn hơn Lưu ý: Trong bpt (6) ta phải viết Lưu ý chung * Khi giải pt mũ bằng phương pháp đặt ẩn số phụ cần chú ý đặt điều kiện cho ẩn số phụ *Khi giải bpt mũ và bpt lôgarit cần chú ý đến cơ số và nắm chắc tính đơn điệu của hs mũ,hs logarit *Một số bài tập giải pt, bpt mũ và logarit bằng phương pháp loogarit hóa hoặc sử dụng tính đơn điệu của h/s mũ,h/s logarit được cho trong phần bài tập tự luyện (có hướng dẫn hoặc đáp số) Bài 1: Giải các phương trình sau b) d) 2x + 4 + 2x + 2 = 5x +1 + 3.5x Bài giải Vậy phương trình có nghiệm x = 1 và x = -4. b) Vậy phương trình có nghiệm x = - 1 và x = 2 Vậy phương trình có nghiệm x = 2. d) 2x + 4 + 2x + 2 = 5x +1 + 3.5x Vậy phương trình có nghiệm x = 1. Bài 2: Giải các phương trình sau e) Bài giải Đặt . Phương trình trở thành: Vậy phương trình có hai nghiệm x = 0 và x = 2. Đặt Phương trình trở thành: Vậy phương trình đã cho có nghiệm . Đặt Phương trình trở thành: Vậy phương trình có nghiệm x = 2. Đặt Phương trình trở thành Vậy phương trình có nghiệm x = -1 và x = 1. e) do nên Đặt , t > 0 ta có pt Vậy phương trình có nghiệm x = -1 và x = 1. Bài 3: Giải các phương trình sau c) Bài giải (1) Điều kiện: x > 0. Vậy phương trình có nghiệm x = 64. (2) Điều kiện: x > 0. Vậy phương trình có nghiệm . c) (3) Điều kiện: x > 0 và x 1 (3) x +1 2 = x2 x2 - x - 12 = 0 Vậy phương trình có nghiệm x = 4 Vậy phương trình có nghiệm x = 5. (5) Điều kiện: x > 0. Đặt . Vậy phương trình có nghiệm x = 4 và x = 8. (6) Điều kiện x > 0. (6’) Đặt Vậy phương trình có nghiệm và (7) Điều kiện x > 0 Đặt Vậy phương trình có hai nghiệm x = 27 và . (8) Điều kiện 3x - 1 > 0 x > 0 (8) Đặt ta có pt : t ( 1 + t ) = 6 t2 + t - 6 = 0 Với t = 2 ta có (nhận) Với t = -3 ta có (nhận) Vậy phương trình có 2 nghiệm x = log310 và Bài 4: Giải các bất phương trình sau: e) g) Bài giải Vậy tập nghiệm của bất phương trình là S = [; 1]. Vậy tập nghiệm của bất phương trình là S = (1) Đặt Bất phương trình trở thành: Kết hợp điều kiện ta được Vậy bất phương trình có tập nghiệm S = (0; 1). e) . Đặt t = , t > 0 ta có bpt 5t2 - 7t + 2 0 t 1 Kết hợp điều kiện ta được t 1 Vậy bất phương trình có tập nghiệm S = [0; 1] g) Đặt ta có bpt: t - + 8 > 0 t2 +8t - 9 > 0 Kết hợp điều kiện ta được t > 1 3x > 1 x > 0 Vậy bất phương trình có tập nghiệm S = (0;) Bài 5: Giải các bất phương trình sau: e) 2log3(4x-3) + f) log2(x+2) + Bài giải Điều kiện Kết hợp điều kiện, bất phương trình có tập nghiệm Điều kiện Kết hợp điều kiện bất phương trình có tập nghiệm (3) Cách 1(Đặt điều kiện) Điều kiện: Kết hợp với điều kiện, bất phương trình có tập nghiệm Cách 2 : Ta có thể viết (3) 2x + 4 x2 - x - 6 > 0 Vậy bất phương trình có tập nghiệm Cách 2: 0 < 7x + 1 10x2 -11x +1 hoặc Vậy tập nghiệm của bất phương trình là Cách 1(đặt điều kiện) Điều kiện: Kết hợp điều kiện, bất phương trình có tập nghiệm e) 2log3(4x-3) + (5) Điều kiện (5) Kết hợp điều kiện, bất phương trình có tập nghiệm S = (; 3] f) log2(x+2) + (6) Điều kiện (6 log2(x+2) + Kết hợp điều kiện bất phương trình có nghiệm CÁC BÀI TẬP TỰ LUYỆN Bài 1: Tính a) b) ĐS : a) 40 b) Bài 2: Rút gọn các biểu thức a) b) ĐS : a) b) a Bài 3: Tính giá trị của các biểu thức a) b) c) d) ĐS : a) 6 ; b) ; c) 144 ; d) 15 Bài 4: Rút gọn các biểu thức a) A = b) B = ĐS : a) 1 ; b) 2(ln2a + 1 ) Bài 5: a, Chứng minh ; b) c) So sánh các số và ; d) HD: a) So sánh và HD: c) 5>3 => log35>log33 = 1 d) 4>1=>log34>log31 = 0 4log74 log4 < log41 =0 => > => Bài 6: Tính đạo hàm của các hàm số a) y = 5x2 + lnx - 7.3x ; b) y = x.ex ; c) d) ĐS: a) y' = 10x + - 7.3x.ln3 ; b) y' = ex (x + 1) c) y' = ; d) y' = Bài 7: Cho hàm số chứng minh xy'+ 1 = ey HD: y' = -; xy'+ 1 = = Bài 8: Giải các PT sau a, b, c) d) e) 25x - 7.5x + 6 = 0 f) 32x+1 - 5.3x + 2 = 0 h) i) k) l) m) n) ĐS: a) x=0 ,x=5 ; b) x=2 ; c) ptvn ; d) x=2 ; e) x=0, x=log56 ; f) x=0,x=log32 -1 ; h) x=0 ; i) x=1, x=3 ; k) x=0,x=; l) x=2, x=0 m) x=0 ; n) x = 1, x= Bài 9: Giải phương trình và bất pt sau a) b) c) ĐS: a) x = (log35 - 5) ; HD: lấy lôgarit cơ số 3 hai vế pt b) x = 2+log52 ; x = 3. HD: lấy lôgarit cơ số 5 hai vế pt rồi biến đổi về pt bậc hai có c) x>4. HD: Viết 62x+3 = 22x+3.32x+3 Bài 10 : Giải các bất phương trình sau a) b) c) d) 9x - 5.3x + 6 < 0 ; e) ; g) ĐS: a) x 2 ; b) ; c) ; d) e) HD đặt t = , t > 0 g) 3 4 . HD: lô ga rít hóa cơ số 10 hai vế bpt ta được (2x2 - 7x).log(x - 3) > 0 .Lập bảng xét dấu vế trái . Bài 11: Giải phương trình sau a) b) c) ĐS: a) x=2 . HD : Dự đoán x = 2 là nghiệm .Ta CM x =2 là nghiệm duy nhất . Chia hai vế của (a) cho 5x ta có pt (1) +) Với x > 2 ta có ; cộng vế với vế hai bpt bên ta có 2 Không là nghiệm của pt (1) +) Với x < 2 làm tương tự ta cũng CM được mọi x < 2 Không là nghiệm của pt (1) Từ đó suy ra x =2 là nghiệm duy nhất b) x = 1 ; c) x < 0 (Câu b và c có thể giải bằng đồ thị) Bài 12 : Giải các PT sau a) b) c) d) e) g) log2(4x +15.2x +27) + = 0 h) i) k) ĐS : a) x = 2; b) x = 8 ; c) x = 4 ; d) x = 3 , x = ; e) x = 1,x = g) x = log23. HD: ĐK 4.2x - 3 > 0 ta có pt log2(4x +15.2x +27) = h) x =1 ; i) x = 2 k) x = 2 là nghiệm. HD Làm tương tự như câu a) bài 11 Bài 13: Giải BPT sau a, b) c) d) e) g) h) ĐS: a) -14 4; b) x < 1; c) -4 x < -1; d)hoặc ; e) hoặc x > 27 g)0 ln2 . (HD: ) Bài 14: Giải hệ phương trình sau a) b) c) d) e) ĐS: a) HD: Rút x ở pt (2) thế vào pt (1) b) và HD: Đặt c) và d) e) HD: Đặt
Tài liệu đính kèm:
 Giao an on thi tn phan PT mu.doc
Giao an on thi tn phan PT mu.doc





