Các bài toán liên quan đến tham số - Các phương pháp giải thường sử dụng

CÁC BÀI TOÁN LIÊN QUAN ĐẾN THAM SỐ
Các phương pháp giải thường sử dụng
Phương pháp 1: Phương pháp đại số. 
Sử dụng các phép biến đổi tương đương thích hợp để tìm số nghiệm
Ví dụ: Tìm m để hệ phương trình sau có nghiệm: 
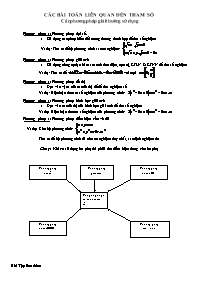
Phương pháp 1: Phương pháp giải tích
Sử dụng công cụ đạo hàm xét tính đơn điệu, cực trị, GTLN & GTNN để tìm số nghiệm
 Ví dụ: Tìm m để với mọi 
Phương pháp 1: Phương pháp đồ thị
Dựa vào vị trí của các đồ thị để để tìm nghiệm số
 Ví dụ: Biện luận theo m số nghiệm của phương trình: 
Phương pháp 1: Phương pháp hình học giải tích
Dựa vào các đồ thị của hình học giải tích để tìm số nghiệm
 Ví dụ: Biện luận theo m số nghiệm của phương trình: 
Phương pháp 1: Phương pháp điều kiện cần và đủ
	 Ví dụ: Cho hệ phương trình: 
	 Tìm m để hệ phương trình đã cho có nghiệm duy nhất, xác định nghiệm đó
Chú ý: Khi có sử dụng ẩn phụ thì phải tìm điều kiện đúng cho ẩn phụ
Pt,bpt,hpt, hbpt có chứa tham số
Phương pháp
đồ thị GT
Phương pháp
đại số
Phương pháp
đồ thị HHGT
Phương pháp
giải tích
Phương pháp
cần và đủ
Bài Tập làm thêm
Bài 1. Tìm m để với mọi 
Bài 2. Tìm m để phương trình sau có nghiệm:
Bài 3. Định m để phương trình : 
 có nghiệm 
Bài 4. Cho bất phương trình : (1)
 Tìm m để bất phương trình (1) có nghiệm. 
Bài 5. Cho phương trình : (1)
 Tìm m để phương trình (1) có nghiệm thuộc khoảng (0;1).
Bài 6. Cho hàm số: 
 Tìm m để phương trình có nghiệm thuộc 
Bài 7. Tìm tất cả các giá trị của m sao cho ta có:
Bài 8. Tìm m để bất phương trình sau đúng với mọi x 
Bài 9. Cho phương trình : 
 Tìm tất cả các giá trị của m để phương trình có nghiệm.
Bài 10. Xác định m để phương trình :
 có ít nhất một nghiệm thuộc đoạn 
Bài 11. Cho phương trình : (1)
 Tìm tất cả các giá trị của m để phương trình (1) có nghiệm.
Bài 12. Cho bất phương trình : (1) 
 Tìm m để bất phương trình nghiệm đúng với mọi x .
Bài 13. Tìm m để phương trình : có nghiệm.
Bài 14. Tìm tất cả các giá trị của tham số m để phương trình: 
 có nghiệm thuộc đoạn [0;1].
Bài 15. Cho phương trình : 
 Với giá trị nào của m thì phương trình có nghiệm.
Bài 16. Cho phương trình 
 Định m để phương trình có nghiệm .
Bài 17. Cho hàm số 
 Tìm m để với mọi 
Bài 18. Tìm m để phương trình : 
 có nghiệm trên đoạn 
Bài 19. Cho phương trình : 
 Tìm m để phương trình có nghiệm.
Bài 20. Cho bất phương trình: (1)
 Tìm m để có nghiệm x
Bài 21. Tìm m để phương trình sau có hai nghiệm trái dấu: 
Bài 22. Tìm m để phương trình sau có nghiệm:
Bài 23. Tìm m để phương trình : có nghiệm thuộc [32;)
Bài 24. Cho bất phương trình : 
 Xác định m để bất phương trình thỏa mãn với mọi x
Bài 25. Cho phương trình: 
 Tìm m sao cho phương trình có nghiệm duy nhất trong đọan [0;1]