Bài tập Tích phân từ 2002 -2010

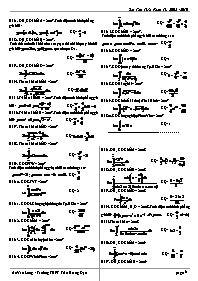
Bài 1. ĐH, CĐ khối A – 2007. Tính diện tích hình phẳng g/h bởi :
 .	 KQ: 
Bài 2. ĐH, CĐ khối B – 2007.
 Tính thể tích của khối trịn xoay tạo thành khi quay hình H g/h bởi:, . quanh trục Ox.	 KQ: 
Bài 3. ĐH, CĐ khối D – 2007
 	 KQ: 
Bài 4. Tham khảo khối A – 2007 
 	 KQ: 
Bài 5. T/khảo khối B – 2007. Tính diện tích hình phẳng g/h bởi : . 	 KQ: 
Bài 6. T/khảo khối B – 2007. Tính diện tích hình phẳng gh bởi:.	 KQ: 
Bài 7. Tham khảo khối D – 2007
	 KQ: 
Bài 8. Tham khảo khối D – 2007
	KQ: 
Bài 9. CĐSPTW – 2007 
Tính diện tích hình phẳng g/hạn bởi các đường sau:
 ; . 	KQ: 
Bài 10. CĐ GTVT – 2007 
	 KQ: 2
Bài 11. CĐDL Cơng nghệ thơng tin Tp.HCM – 2007 
	KQ: 
Bài 12. CĐ Khối A – 2007 
	 KQ: 
Bài 13. CĐ Cơ khí luyện kim – 2007 
	 KQ: 
Bài 14. CĐSP Vĩnh Phúc – 2007 
	 KQ: 
Bài 15. CĐ Khối B – 2007.
 Tính diện tích hình phẳng g/h bởi các đường sau
 , , , . 	KQ: 
Bài 16. CĐ Khối D – 2007 
	KQ: 1
Bài 17. CĐ Dệt may thời trang Tp.HCM – 2007 
	 KQ: 
Bài 18. CĐ Hàng hải – 2007 
	KQ: 
Bài 19. CĐ Kinh tế kĩ thuật Thái Bình – 2007 
	 	KQ: 
Bài 20. CĐ Cơng nghiệp Phúc Yên – 2007 
	KQ: 1
-------------------------------------------------------------
Bài 1. ĐH, CĐ Khối A – 2008 
 	 KQ: 
Bài 2. ĐH, CĐ Khối B – 2008
 	KQ: 
Bài 3. ĐH, CĐ Khối D – 2008
	 KQ: 
Bài 4. CĐ Khối A, B, D – 2008. Tính diện tích hình phẳng g/h bởi: và . KQ: (đvdt)
Bài 5. Tham khảo – 2008
 KQ: 
Bài 6. ĐH, CĐ Khối A – 2009 
 KQ: 
Bài 7 . ĐH, CĐ Khối B – 2009 
 KQ: 
Bài 8. ĐH, CĐ Khối D – 2009 
 KQ: 
Bài 9. CĐ Khối A, B, D – 2009 
 KQ: 
Bài 10. ĐH, CĐ Khối A – 2010 
 KQ: 
Bài 11 . ĐH, CĐ Khối B – 2010 
 KQ: 
Bài 12 . ĐH, CĐ Khối D – 2010 
 KQ: 
Chúc các em ơn tập tốt.
Mọi gĩp ý xin gửi về Website
An Văn Long – THPT Trần Hưng Đạo
DIỆN TÍCH HÌNH PHẲNG
Bài 1: Tính diện tích hình phẳng giới hạn bởi:
1) (C) : y = x2 – 4x + 3 ; trục Ox ; x = 0 và x = 4.
2) (C) : y = x – x2 và trục Ox.
3) (C) : y = – x2 + 4x – 3 và các tiếp tuyến với đường cong này tại các điểm A(0,–3) và B(3,0).
4) (C) : y = Sinx ; trục Ox ; và 
5) (C) : y = 2x2 – 4x – 6 ; x = –2 và x = 4.
6) (C) : y = lnx ; trục Ox ; và x = e.
7) (C) : y = ; trục Ox ; x = 2 ; x = 4.
8) (C) : ; trục Ox.
9) (C) : x = 4 – y2 ; trục Oy ; y = –2 và y = 2.
10) (C) : x = y2+ 4y ; trục Oy.
Bài 2: Tính diện tích hình phẳng giới hạn bởi:
(C) : y = x2 + 2x ; (D) : y = x + 2.
 (C) : y = ; tiệm cận xiên của (C) và hai đường thẳng x = 2; x = 4 
(C) : y = x2 – 2x và hai tiếp tuyến với (C) tại các điểm O(0,0) ; A(3,3).
y = Sin3x ; y = Cos3x ; x = 0 ; x = 
(P) : y2 = 2x và đường thẳng d: 2x – y – 2 = 0.
(C) : y2 – 24x = 48 và y = 16 – 8x.
Bài 3: Cho . Hai điểm A, B di động trên (P) : AB = 2
Tìm tập hợp trung điểm I của AB.
Xác định A , B sao cho diện tích của phần mặt phẳng giới hạn bởi AB và (P) đạt giá trị lớn nhất.
Bài 4: Xét hình có diện tích chắn bởi và đường thẳng có hệ số góc k đi qua điểm . Xác định k để diện tích đó lớn nhất.
Bài 5: Cho và 
Tìm R để (C) tiếp xúc với (P). Xác định tọa độ các tiếp điểm T và T’.
Viết phương trình tiếp tuyến chung của (P) và (C) tại T và T’.
Tính diện tích tam giác cong giới hạn bởi (P) và 2 tiếp tuyến nói trên.
Bài 6: Parabol chia diện tích của hình tròn tâm O(0,0) bán kính R = theo tỉ số nào.
THỂ TÍCH VẬT THỂ
Bài 1: Tính thể tích các vật thể tạo nên khi quay quanh Ox hình phẳng S với S được giới hạn bởi: 
	1) (C) : y = 2x – x2 và trục Ox. 
	2) S là (E) : 
	3) S là x2 + (y – b)2 = a2 
	4) (C) : y = x2 ; y = 0 ; x = 0 ; x = 1.
	5) (C) : y = x2 – 2x ; y = 0 
	6) (C) : y = ; trục Ox ; x = 0 ; x = 
	7) (C) : y = ; trục Ox ; x = 0 ; x = 2 
	8) (C1) : y = x2 ; (C2) : y = 2x.
	9) y = 0 ; ; x = 0 ; x = 
	10) Hình tròn: x2 + (y – 2)2 £ 1
(C): y = x.lnx , y = 0 , x = 1 , x = e
y = lnx , y = 0, x = 1 , x = 2
y = 0 , , , 
 , y = 0 , x = 0 và 
Bài 2: Miền D g/hạn bởi y2 = (4 – x)3 và y2 = 4x.
Tính diện tích miền D.
Tính thể tích tròn xoay do D quay quanh Ox.
Bài 3: Gọi (D) là miền giới hạn bởi các đường , và parabol .Tính TT tròn xoay do ta quay (D) quanh trục Ox tạo nên ((D) nằm ngoài (P))
Bài 4: Gọi miền giới hạn bởi các đường y = 0 , là (D). Tính thể tích vật thể được tạo thành do ta quay (D) :
Quanh trục Ox.
Quanh trục Oy
Bài 5: Cho hình tròn có tâm I(2 , 0) , bán kính R = 1 , quay quanh trục Oy. 	Tính thể tích của vật thể tròn xoay được tạo nên
.Hết