Bài tập Bất phương trình - Bất phương trình mũ

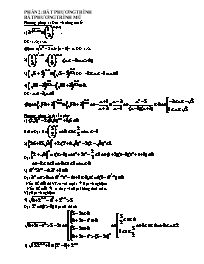
PHẦN 2: BẤT PHƯƠNG TRÌNH
BẤT PHƯƠNG TRÌNH MŨ
Phương pháp 1: Đưa về cùng cơ số:
1) . 
ĐK: x≥2; x≤0.
. ĐS: x≥2.
2) 
3) . ĐS: 
4) . 
ĐK: 
Phương pháp 2: đặt ẩn phụ:
1) .
Hdẫn: Đặt 
2) .
Đặt 
3) 
Đặt 
+Nếu thì VT>0 với mọi t à Bpt vô nghiệm
+ Nếu àx=0 thay vào Bpt không thoả mãn.
Vậy Bpt vô nghiệm
4) 
Đặt . Bpt trở thành
5) 
Đặt . Bất phương trình trở thành:
6) 
Đk: 
Bất phương trình tương đương 
Đặt giải được 
7) 
Đặt bất phương trình trở thành 
ĐS: 
8)
Đặt 
9) 
Đặt 
Bpt trở thành : 
u<vàx<1.
Phương pháp 3: Phân tích thành nhân tử
1) 
2) 
ĐS : 
3) 
4) 
Đặt bất pt trở thành 
ĐS : 
Phương pháp 4: Sử dụng tính đơn điệu của hàm số
1) 
Xét hàm số 
Lập BBTta có f(x)≤0 với mọi x thuộc R. Do đó , bpt 
2) .
Hdẫn: ; f(x) là HSNB và f(2)=0
g(x) là HSĐB và g(1/2)=0
Lập bảng xét dấu
x
-∞ ½ 2 +∞
f(x)
 + | + 0 -
g(x)
 - 0 + | +
f(x)/g(x)
 - || + 0 -
ĐS : 
3) 
Áp dụng bđt cô si thì VT. Giải được 
4) 
Bất phương trình tương đương 
ĐS : x2
5) Tìm m để BPT sau có nghiệm 
Cách 1 : Sử dụng tam thức bậc 2.
Cách 2 : 
+t=1
+t>1 : 
+t<1 : 
6) Tìm m để Bpt sau nghiệm mọi x : 
Đặt 
. Lập BBTta được m≥1.
7) Tìm m để bpt sau nghiệm mọi x thoả mãn :  : .
Đặt >Btoán trở thành tìm m để bpt sau nghiệm mọi t≥1 : 
+t=1
+t>1 : 
ĐS :m≤0
C¸c bµi to¸n tæng hîp vÒ bÊt ph­¬ng tr×nh mò
Bµi 1: Gi¶i c¸c bÊt ph­¬ng tr×nh:
a) 	b) 
c) 	d) 
Bµi 2: Gi¶i c¸c bÊt ph­¬ng tr×nh :
a) 	b) 
c) 	d) 
Bµi 3: Gi¶i c¸c bÊt ph­¬ng tr×nh:
a) 	b) 
c) 	d) 
Bµi 4: Gi¶i c¸c bÊt ph­¬ng tr×nh:
a) 	b) 
 c) d) 
1) 	
2) 
3) 
4) 	
5) 
6) 
 7) 
8) 
 9) 
10) 
 11)