Giáo án môn Giải tích 12 tiết 35: Khảo sát hàm số. Bài tập
Tiết 35
. Ổn định lớp :
Ổn định trật tự, kiểm diện sĩ số.
. Kiểm tra :
. Nội dung bài mới:
(4 ) Khảo sát hàm số trùng phương :
y = ax4 + bx2 + c a 0
a) Các thí dụ cụ thể :
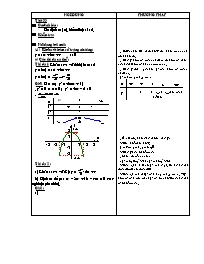
Thí dụ 1 Khảo sát và vẽ đồ thị hàm số
y = f(x) = ax4 + bx2 + c
Bạn đang xem tài liệu "Giáo án môn Giải tích 12 tiết 35: Khảo sát hàm số. Bài tập", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
NỘI DUNG PHƯƠNG PHÁP x y’ y” y -¥ +¥ 0 0 - + - -¥ -¥ 3/2 -5/2 1 2 3 -1 -2 -3 1 2 -1 -2 x y x y -¥ +¥ +a 0 a 0 0 đổi dấu 0 dấu của a Tiết 35 . Ổn định lớp : Ổn định trật tự, kiểm diện sĩ số. . Kiểm tra : . Nội dung bài mới: (4 ) Khảo sát hàm số trùng phương : y = ax4 + bx2 + c a ¹0 a) Các thí dụ cụ thể : Thí dụ 1 Khảo sát và vẽ đồ thị hàm số y = f(x) = ax4 + bx2 + c y = f(x) = Giải D = ; y’ = -2x(x2 + 1) . y’ = 0 Û x = 0 ; y” = -6x2 – 2 < 0 . Thí dụ 2 : a) Khảo sát và vẽ (C) : y = - 2x2 + 4 b) Định m để pt : x4 – 8x2 + 16 – 4m = 0 có 4 nghiệm phân biệt. Giải : a) x y’ y” y -¥ +¥ 0 0 - + - +¥ +¥ -2 -2 2 2 0 + 0 - + 0 + 0 0 CT 4 CĐ U 16/9 16/9 0 Giải BT b) b) Khảo sát tổng quát : . Miền xác định D = ; y’ = 2x (2ax2 + b) . y” = 12ax2 + 2b ; . Dấu y’, y” phụ thuộc a và b nên có 4 trường hợp a> 0 (a > 0, b ³ 0) (a 0, b 0) . Củng cố : . Học sinh cần nắm vững các dạng của đồ thị. Hình dạng đồ thị phụ thuộc vào các hằng số a, b. . Dựa vào khảo sát tổng quát hãy phát họa sơ lược hình dạng đồ thị các hàm số. a) y = x4 – 5x2 + 4 b) y = -x4 – 2x2 + 3 . Chú ý cách xét dấu của y’ . Dặn dò : . Hướng dẫn HS thực hiện các khâu trong quá trình khảo sát. . Chú ý hàm số trùng phương là hàm số chẵn nên đồ thị hàm số đi qua trục tung. . Chú ý cách xét dấu y’ của hàm số trùng phương. y’ = 0 Û x = 0, x = ± a . Ở ví dụ 2, khi vẽ đồ thị cần chú ý : + Các điểm đặc biệt. y = 4 Û x = 0 , x ¹ 2 + Chú ý đến 2 điểm uốn . Khảo sát tổng quát : - y’ = 2x(2ax2 + b) ; y” = 12ax2 + 2b + Nếu a.b ³ 0 (hoặc y” < 0 "x). Do đó đồ thị luôn lõm (hoặc luôn lồi) + Nếu a.b < 0 thì y’ có 3 do x = 0. x = ± a. Vậy hàm số có 3 cực trị và y” có 2 nghiệm nên đồ thị có 2 điểm uốn. a < 0 D. RÚT KINH NGHIỆM:
Tài liệu đính kèm:
 C2-35.doc
C2-35.doc





