Giáo án Giải tích 12 - Tiết 3 đến tiết 72

Tiết 3+4
CỰC TRỊ CỦA HÀM SỐ
Ngày soạn: 6/8/2008
Ngày dạy: 9/8/2008
I-Mục tiêu:
+ Về kiến thức:
Nắm vững định lí 1 và định lí 2
Phát biểu được các bước để tìm cực trị của hàm số (quy tắc I và quy tắc II)
+ Về kỹ năng:
 Vận dụng được quy tắc I và quy tắc II để tìm cực trị của hàm số
+ Về tư duy và thái độ:
Áp dụng quy tắc I và II cho từng trường hợp 
Tích cực học tập, chủ động tham gia các hoạt động
II. – Chuẩn bị
	+ GV: Giáo án, bảng phụ.
	+ HS: SGK, đọc trước bài học
III- Tiến trình bài giảng:
ổn định tổ chức
Kiểm tra bài cũ
Câu hỏi: Nêu qui tắc xét tính đơn điệu của hàm số
 Áp dụng xét tính đơn điệu của hàm số sau: 
 3- Nội dung bài mới
HĐ của thầy và trò
Nội dung ghi bảng
 Hoạt động 1
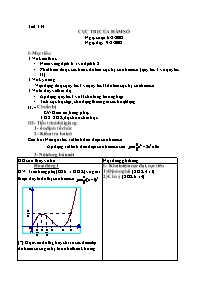
GV: Treo bảng phụ (H8 tr 13 SGK) và giới thiệu đây là đồ thị của hàm số 
(?) Dựa vào đồ thị, hãy chỉ ra các điểm tại đó hàm số có giá trị lớn nhất trên khoảng ? 
(?) Dựa vào đồ thị, hãy chỉ ra các điểm tại đó hàm số có giá trị nhỏ nhất trên khoảng ? 
HS: Lĩnh hội câu hỏi quan sát đồ thị và trả lời
GV: chính xác hoá câu trả lời và giới thiệu điểm đó là cực đại (cực tiểu).
HS: Chú ý lắng nghe lĩnh hội ki ến thức mới
 Hoạt động 2
GV: Yêu cầu HS xem lại đồ thị ở bảng phụ và bảng biến thiên của nó
(?) Nêu mối liên hệ giữa tồn tại cực trị và dấu của đạo hàm?
 GV: chính xác hoá kiến thức, từ đó dẫn dắt đến nội dung định lí 1 SGK
HS: Chú ý lắng nghe lĩnh hội ki ến thức mới
 Hoạt động 3
GV: Dùng phương pháp vấn đáp cùng với HS giải vd như SGK.
HS: trả lời câu hỏi
GV: Cho HS nghiên cứu vd2, vd3 rồi g ọi 2 hs lên bảng trình bày.
HS: lên bảng trình bày
GV:Cho HS khác nhận xét và GV chính xác hoá lời giải.
GV: theo dõi bài giải và trả lời
Hoạt động 4
GV:Yêu cầu HS nêu các bước tìm cực trị của hàm số từ định lí 1
HS: trả lời
GV: treo bảng phụ ghi quy tắc I
 Yêu cầu HS tính thêm y”(-), y”(1) ở vd2 trên
HS: Thực hành
 (?)Quan hệ giữa đạo hàm cấp hai với cực trị của hàm số?
HS: trả lời
GV :thuyết trình và treo bảng phụ ghi định lí 2, quy tắc II
Hoạt động 5
GV: hãy áp dụng qui tắc II để tìm cực trị của các hàm số sau
 hướng dẫn cụ thể các bước giải cho học sinh
(?)Nêu TXĐ và tính y’ 
(?)giải pt y’ =0 và tính y’’=?
HS: Ghi nhận và làm theo sự hướng dẫn của GV
GV : Gọi 1 HS lên bảng
tính y’’()=? y’’() =? nhận xét dấu của chúng ,từ đó suy ra các cực trị của hàm số 
 HS: lên bảng giải
GV: Gọi 1 HS khác nhận xét 
 Chính xác hoá và cho lời giải
HS:Nhận xét bài làm của bạn và ghi nhận kq
I.- Khái niệm cực đại, cực tiểu
1) Định nghĩa (SGK-tr 13)
2) Chú ý (SGK tr 14)
II. Điều kiện đủ để hàm số có cực trị
1) Định lí 1 (SGK tr 14)
x
x0-h x0 x0+h
F’(x)
 + -
F(x)
 fCD
2- Ví dụ:
* Ví dụ 1: Tim cực trị của hàm số
x
x0-h x0 x0+h
F’(x)
 - +
F(x)
 fCT
* Ví dụ 2:Tìm các điểm cực trị của hàm số: 
* Ví dụ 3: tìm cực trị của hàm số:
III-Quy tắc tìm cực trị:
1) Quy tắc I: sgk/trang 16
2)Định lí 2: sgk/trang 16
*Quy tắc II: sgk/trang 17
*Ví dụ 1:
Tìm các điểm cực trị của hàm số:
 f(x) = x4 – 2x2 + 1
 Giải:
Tập xác định của hàm số: D = R
f’(x) = 4x3 – 4x = 4x(x2 – 1)
f’(x) = 0 ; x = 0
f”(x) = 12x2 - 4
f”(1) = 8 >0 x = -1 và x = 1 là hai điểm cực tiểu
f”(0) = -4 < 0 x = 0 là điểm cực đại
Kết luận:
f(x) đạt cực tiểu tại x = -1 và x = 1; 
fCT = f(1) = 0
f(x) đạt cực đại tại x = 0; 
fCĐ = f(0) = 1
*Ví dụ 2:
Tìm các điểm cực trị của hàm số
 f(x) = x – sin2x
Giải:
Tập xác định : D = R
f’(x) = 1 – 2cos2x
f’(x) = 0 cos2x = 
 (k)
f”(x) = 4sin2x
f”() = 2 > 0
f”(- ) = -2 < 0
Kết luận:
x = ( k) là các điểm cực tiểu của hàm số
x = -( k) là các điểm cực đại của hàm số
4. Củng dặn dò: 
 Các mệnh đề sau đúng hay sai?
1/ Số điểm cực tr ị của hàm số y = 2x3 – 3x2 là 3
2/ Hàm số y = - x4 + 2x2 đạt cực trị tại điểm x = 0
 Đáp án: 1/ Sai
 2/ Đúng
Hướng dẫn học bài ở nhà và ra bài tập về nhà:
Định lý 2 và các quy tắc I, II tìm cực trị của hàm số
BTVN: làm các bài tập còn lại ở trang 18 sgk
Đọc bài và tìm hiểu bài mới trước ở nhà
Tiết 5 BÀI TẬP CỰC TRỊ CỦA HÀM SỐ
Ngày soạn: 22/8/2008
Ngày dạy: 25/8/2008
I. MỤC TIÊU:
1/ Kiến thức: 
	+Khắc sâu khái niệm cực đại ,cực tiểu của hàm số và các quy tắc tìm cực trị của hàm số
2/ Kỹ năng: 
	+Vận dụng thành thạo các quy tắc để tìm cực trị của hàm số 
	+Sử dụng thành thạo các điều kiện đủ và chý ý 3 để giải các bài toán liên quan đến cực trị của hàm số 
3/ Tư duy: Biết chuyển hoá qua lại giữa kiến thức từ trực quan (hình vẽ) và kiến thức từ suy luận logic.
 II – Chuẩn bị
GV: giáo án, bảng phụ
HS: học bài cũ và xem trước bài mới ở nhà
II- Tiến trình bài giảng:
1-ổn định tổ chức
2-Kiểm tra bài cũ
Câu hỏi: Nêu các quy tắc để tìm cực trị của hàm số 
 Áp dụng tìm cực trị của hàm số sau 
 3- Nội dung bài mới
HĐ của thầy và trò
Nội dung ghi bảng
Hoạt động 1
Ghữa bài tập 1
GV: Chép đề bài lên bảng
gọi 2 HS xung phong lên bảng giải
HS: lên bảng trình bày
GV:Gọi HS khác nhận xét 
 Chính xác hoá và cho lời giải
HS:Nhận xét bài làm của bạn và ghi nhận kq
Hoạt động 2
Ghữa bài tập 2
GV hướng dẫn cụ thể các bước giải cho học sinh
(?)Nêu TXĐ và tính y’ 
(?)giải pt y’ =0 và tính y’’=?
HS: Ghi nhận và làm theo sự hướng dẫn của GV
GV : Gọi 1 HS lên bảng
tính y’’()=? y’’() =? nhận xét dấu của chúng ,từ đó suy ra các cực trị của hàm số 
HS xung phong lên bảng giải
GV: Gọi 1 HS khác nhận xét 
 Chính xác hoá và cho lời giải
HS:Nhận xét bài làm của bạn và ghi nhận kq
Hoạt động3
Ghữa bài tập 3
GV: Hãy cho biết TXĐ và tính y’
HS: Lĩnh hội câu hỏi nháp và trả lời
GV: (?) Nêu điều kiện cần và đủ để hàm số đã cho có 1 cực đại và 1 cực tiểu,từ đó cần chứng minh >0, R
HS: đứng tại chỗ trả lời câu hỏi
bài tập 1
AD quy tắc I,hãy tìm cực trị của các hàm số 
1/ 2/
 Giải:
1/ TXĐ: D = \{0}
Bảng biến thiên
 X
 -1 0 1 
 Y’
 + 0 - - 0 +
Y
 -2 
 2
Hàm số đạt cực đại tại x= -1, yCĐ= -2
Hàm số đạt cực tiểu tại x =1, yCT = 2
2/ TXĐ D=R
 có tập xác định là R
X
 y’
 - 0 +
Y
hsố đạt cực tiểu tại x =, yCT = 
bài tập 2
Tìm cực trị của hàm số y = sin2x-x
TXĐ D =R
;
y’’= -4sin2x , y’’() = -2<0,
hsố đạt C Đ tại x=, yCĐ=
y’’() =8>0, hsố đạt CT tại x=,yCT=
bài tập 3
Chứng minh rằng với mọi giá trị của tham số m,hàm số 
y =x3-mx2 –2x +1 luôn có 1 cực đại và 1 cực tiểu
TXĐ: D =R.
y’=3x2 -2mx –2
Ta có: = m2+6 > 0, R 
pt y’ =0 có 2 nghiệm phân biệt R
đpcm
4- củng cố: bài học này HS cần khắc sâu
 -Quy tắc I thường dùng tìm cực trị của các hàm số đa thức,hàm phân thức hữu tỉ.
 Quy tắc II dùng tìm cực trị của các hàm số lượng giác và giải các bài toán liên đến cực trị
Tiết 6+7
GIÁ TRỊ LỚN NHẤT NHỎ NHẤT CỦA HÀM SỐ
Ngày soạn: 5/9/2008
Ngày dạy: 6/9/2008
I. MỤC TIÊU:
Về kiến thức:
Nắm được ĐN, phương pháp tìm gtln, nn của hs trên khoảng, nửa khoảng, đoạn.
Về kỹ năng:
Tính được gtln, nn của hs trên khoảng, nửa khoảng, đoạn.
Vận dụng vào việc giải và biện luận pt, bpt chứa tham số.
Về tư duy, thái độ:
Rèn luyện tư duy logic, tư duy lý luận.
Tích cực, chủ động nắm kiến thức, tham gia xây dựng bài.
II. – Chuẩn bị
	+ GV: Giáo án, bảng phụ.
	+ HS: SGK, đọc trước bài học
III- Tiến trình bài giảng:
1-ổn định tổ chức
2-Kiểm tra bài cũ
Câu hỏi: Cho hs y = x3 – 3x.
Tìm cực trị của hs.
Tính y(0); y(3) và so sánh với các cực trị vừa tìm được.
GV nhận xét, đánh giá. 
 3- Nội dung bài mới
HĐ của thầy và trò
Nội dung ghi bảng
Hoạt động 1:
Hình thành ĐN GTLN, GTNN.
GV: Hãy quan sát BBT (ở bài tập kiểm tra bài cũ) và trả lời các câu hỏi
( ?) 2 có phải là gtln của hs trên [0;3]
( ?) Tìm 
 HS: Lĩnh hội câu hỏi nháp và trả lời
GV: Chính xác hoá ĐN GTLN, GTNN như trong sgk
HS: lĩnh hội và ghi nhớ kiến thức mới
Hoạt động 2:
GV: Hướng dẫn thông qua các câu hỏi cụ thể
(?) Hãy tìm TXĐ của hàm số
(?) Hãy Lập BBT và tìm gtln, nn của hsố
HS: Lĩnh hội câu hỏi nháp và trả lời
 Hoạt động 3:
 GV: Yêu cầu HSLập BBT và tìm gtln, nn của các hs: 
HS: Lĩnh hội câu hỏi nháp và trả lời
GV:
(?) Hãy nhận xét mối liên hệ giữa liên tục và sự tồn tại gtln, nn của hs trên một đoạn.
HS: trả lời
GV: Nêu ĐL 2
HS: lĩnh hội và ghi nhớ kiến thức mới
GV: Y cầu hs xem ví dụ sgk tr 20
 và giải thích những thắc mắc của hs 
HS: Xem ví dụ sgk tr 20.
Hoạt động 4:
Tiếp cận quy tắc tìm gtln, nn của hsố trên đoạn.
GV: Cho hàm số 
 có đồ thị như hình vẽ sgk tr 21. 
(?) gtln, nn của hs/[-2;1]; [1;3]; [-2;3].
bằng ? ( nêu cách tính )
(?) Nhận xét cách tìm gtln, nn của hs trên các đoạn mà hs đơn điệu như: 
[-2;0]; [0;1]; [1;3].
-(?) Nhận xét gtln, nn của hsố trên các đoạn mà hs đạt cực trị hoặc f’(x) không xác định như: [-2;1]; [0;3].
HS: Nêu vài nhận xét về cách tìm gtln, nn của hsố trên các đoạn đã xét
Hoạt động 5
GV: chép đề bài y cầu HS hoạt đông nhóm để làm bài
HS: thực hiện làm bài theo nhóm cử đai diện lên bảng trình bày
I- Định nghĩa
1) Định nghĩa (SGK tr 19)
2) ví dụ:
* Ví dụ 1: tìm gtln, nn của hs
 Giải
II- Cách tính GTLN, GTNN của hàm số trên một đoạn
1) Đ ịnh l ý:( SGK Tr 20)
*Ví dụ 2:(SGK tr 20)
2) Quy tắc tìm GTLN, GTNN của hàm số trên một đoạn.
a) Quy t ắc : ( SGK tr22)
chú ý: các nghiệm xi của y’ thuộc đoạn cần tìm gtln, nn
b) Ví dụ 3:
 1)áp dụng quy tắc tìm gtln, nn của hàm số
trên(-2;1]; [0;3].
 Giải
* Chú ý sgk tr 22.
4- Củng cố dặn dò 
 Mục tiêu của bài học ghi nhớ quy tắc tìm gtln, nn trên khoảng, đoạn.
Làm bài tập từ 1 đến 5 trang 23, 24 sgk.
Quy tắc tìm gtln, nn trên khoảng, đoạn. Xem bài đọc thêm tr 24-26
Tiết 8
 BÀI TẬPGIÁ TRỊ LỚN NHẤT NHỎ NHẤT CỦA HÀM SỐ
Ngày soạn: 7/9/2008
Ngày dạy: 8 /9/2008
I- Mục tiêu
 +Về kiến thức:
Nắm vững phương pháp tìm GTLN, NN của hàm số trên khoảng, đoạn.
+Về kỹ năng:
Tìm được gtln, nn của hs trên khoảng, đoạn.
+ Về tư duy, thái độ:
Rèn luyện tư duy logic, tư duy lý luận.
Tích cực, chủ động nắm kiến thức, tham gia xây dựng bài.
II. – Chuẩn bị
	+ GV: Giáo án, bảng phụ.
	+ HS: Làm bài t ập trước ở nhà
III - Tiến trình bài giảng:
1-ổn định tổ chức
2-Kiểm tra bài cũ
Câu hỏi: Nêu quy tắc tìm gtln, nn của hàm số trên đoạn. Áp dụng tìm gtln, nn của hs
 y = x3 – 6x2 + 9x – 4 trên đoạn [0;5]; [-2;-1] và trên (-2;3).
GV: Nhận xét, đánh giá.
 3- Nội dung bài mới
HĐ của thầy và trò
Nội dung ghi bảng
Hoạt động 1:
Chữa bài tập 1
GV:Dựa vào phần kiểm tra bài cũ nêu lại quy tắc tìm gtln, nn của hs trên đoạn. Yêu cầu 2 học sinh vận dung lên bảng giải 1b,1c sgk tr 24.
HS : Lên bảng trình bày
GV: Gọi HS khác nhận xét lời giải
HS: trả lời
GV: chính xác lời giải
HS: Lắng nghe và ghi nhận kết quả
Hoạt động 2:
Chữa bài tập 4
a)GV Hướng dẫn thông qua các câu hỏi cụ thể
(?) C ần tìm GTNN,GTNN của hàm số trên tập nào
(?) Cần sdụng cách nào để tìm GTNN,GTNN của hàm số
(?) Hãy tìm TXĐ của hàm số
(?) Hãy lập bảng BT của hàm số từ đó nêu kết luận
HS: Lĩnh hội câu hỏi nháp và trả lời
b) GV cho HS hoạt đông theo nhóm
HS: thực hiện làm bài theo nhóm cử đai diện lên bảng trình bày
Hoạt động 3
Cho học sinh tiếp cận với dạng bài tập tìm gtln , nn trên khoảng.
GV:Cho học sinh làm bài tập: 5b sgk tr 24
HS: thảo luận nhóm
Đại diện nhóm lên bảng trình bày bài giải.
GV: Nhận xét, đánh giá câu 4b, 5b.
Bài tập 1 sgk tr 24.
Tìm GTLN, GTNN của các hàm số sau
1b) trên các đoạn và 
*  ... ủa HS
Ghi bảng
 Hoạt động 1 ( 5 phút)
 Căn bậc hai của số thực âm 
(?) thế nào là căn bậc hai của số thực dương a?
GV ptích từ đẳng thức
 i2 = - 1=> ĐN
(?) Tổng quát căn bậc hai của một số âm a là?
 Hoạt động 2(15 phút)
Pt bậc 2 với hệ số thực
(?) Nhắc lại cách giải pt bậc 2
ax2 + bx + c (a ¹ 0), a, b, c Î R với nghiệm x trên R
(?) Nếu xét trên C 
Khi D < 0, phương trình có nghiệm không?
nghiệm bằng bao nhiêu vì sao?
Ví dụ: giải phương trình
GV trình bày lời giải
 Hoạt động 4:(10 phút)
Giải pt trên tập số phức:
Chia nhóm
Nxét chốt lại kiến thức
đại diện hs trả lời
là số b sao cho 
theo dõi tiếp thu ĐN
đại diện hs trả lời
các căn bậc hai của số thực a âm là :
1 Hs nhắc lại
D = b2 – 4ac.
 + Khi D = 0, phương trình có nghiệm thực: 
+ Khi D > 0, phương trình có 2 nghiệm thực: 
+ Khi D < 0, phương trình vô nghiệm thực. + 
+Khi D < 0 trên C pt có 2 nghiệm là
- Theo dõi ghi nhớ
Thảo luận nhóm để giải các phương trình sau trên tập số phức:
a/ x2 + 2x + 3 = 0
b/ x2 - 3x + 4 = 0
c/ x2 + x + 6 = 0
d/ x2 - 4x + 5 = 0
1. Căn bậc hai của số thực âm:
 Từ đẳng thức i2 = - 1, ta nói i là một căn bậc hai của – 1; và – i cũng là một căn bậc hai của – 1. Từ đó, ta xác định được căn bậc hai của số thực âm. 
Ví dụ: 
+ Căn bậc hai của – 2 là , vì 
+ Căn bậc hai của – 3 là , vì 
+ Căn bậc hai của – 4 là , vì 
Một cách tổng quát, các căn bậc hai của số thực a âm là :
2. Phương trình bậc hai với hệ số thực:
 Trên C cho phương trình bậc 2
ax2 + bx + c (a ¹ 0), a, b, c Î R, 
 có D = b2 – 4ac. 
+ )Khi D = 0, phương trình có nghiệm : 
+ )Khi D > 0, phương trình có 2 nghiệm : 
+ )Khi D < 0 pt có 2 nghiệm là
Ví dụ 1: giải phương trình
 x2 + x + 1 = 0 trên tập số phức.
Giải:
Ta có: D = 1 – 4 = - 3.
Vậy phương trình đã cho có 2 nghiệm phức là:
 Ví dụ 1
 Giải các phương trình sau trên tập số phức:
a/ x2 + 2x + 3 = 0
b/ x2 - 3x + 4 = 0
c/ x2 + x + 6 = 0
d/ x2 - 4x + 5 = 0
IV-Củng cố(5 phút)
 Nhắc lại cách tính căn bậc hai của số thực âm, cách giải phương trình bậc hai với hệ số thực.
tiết 67 
BÀI TẬP PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
Ngày soạn: 15/03/2009 
Ngày dạy:16/03/2009 
I. Mục tiêu:
	+ Về kiến thức: Khi học xong phần này, học sinh hiểu rõ hơn về căn bậc hai của số phức cũng như cách giải phương trình bậc hai trên tập số phức
 + Về kĩ năng: Giúp học sinh rèn luyện kỹ năng về tìm căn bậc hai của số phức và kỹ năng giải phương trình bậc hai trên tập số phức 
 + Về tư duy và thái độ: tích cực hoạt động, có tinh thần hợp tác.
II. Chuẩn bị 
	+ Giáo viên: Giáo án và các tài liệu liên quan
	+ Học sinh: Các kiến thức đã học về định nghĩa căn bậc hai của số phức và công thức nghiệm của phương trình bậc hai trên tập số phức
III. Tiến trình bài dạy:
	1. Ổn định tổ chức(2 phút): Ổn định lớp, điểm danh
	2. Kiểm tra bài cũ(10 phút)
Câu hỏi 1 
Hoạt động của giáo viên
Hoạt động của HS
 Ghi bảng
Câu hỏi 1 
 Định nghĩa căn bậc hai của số thực âm tìm căn bậc hai của các số : -5, -6, -7
Câu hỏi 2 
 Nêu công thức nghiệm của phương trình Az2 +Bz +C = 0, với A, B, C là các số thực và A khác không. 
Áp dụng làm bài 2b tr 140
Một học sinh trả lời và trình bày lời giải
+Một học sinh làm bài trên bảng
+ Căn bậc hai của -5 lài và -i vì (i)2= -5 và 
(-i)2= -5
3- Bài mới
Hoạt động của giáo viên
Hoạt động của HS
Ghi bảng
Hoạt động1(10phút)Chép đề cho hs thảo luận nhóm 
Giải PT: z+=k
với k=1 và k=2i
giáo viên nhận xét và chốt lại kiến thức
Hoạt động 2(10phút)
giải bt 3 tr 140
-Goi 2 hs lên bảng trình bày bt đã chuẩn bị ở nhà
- Gọi hs nhận xét
- chốt lại nội dung kiến thức
Hoạt động 3 (10phút)
giải bt 5 tr 140
(?)z=a+bi thì
 z +=?
 z. =?
(?) pt bậc 2 nhận z và làm nghiệm là pt nào
(?) Hãy đưa pt trên về hệ số thực
Theo dõi nhận xét kết quả
+Một đại diện của nhóm học sinh làm bài trên bảng
HS1
Đặt z=t được pt
=> pt có 4 nghiệm
HS2 
Đặt z=t được pt
+) nhớ lại kiến thức cũ
z +=2a
 z. =a2 + b2
+) Một pt bậc 2 nhận z và làm nghiệm là pt (x-z)(x-)=0
+) Nháp và một hs lên bảng tình bày
Bài 1: Giải PT: z+=k
với k=1 và k=2i
z+=k
Với k= 1 thì = -3
Vậy phương trình có các nghiệm là:và
b. Với k = 2i thì = -8
 Vậy phương trình có các nghiệm là:
,
Bài 3 tr 140
Giải các pt sau
a) 
b)
Giải
Bài 5 tr 140
Cho z=a+bi là một số phức
Tìm pt bậc 2 với hệ số thực nhận z và làm nghiệm
Giải
Một pt bậc 2 nhận z và làm nghiệm là pt (x-z)(x-)=0
4. Củng cố dặn dò(3 phút)
- Khắc sâu định nghĩa căn bậc hai của số thực âm
- Hiểu và nhớ phương pháp giải phương trình bậc hai trên tập số phức
tiết 68 
ÔN TẬP
Ngày soạn: 21/3/2009 
Ngày dạy:23/3/2009 
I. Mục tiêu
 - Kiến thức cơ bản: 
 + Số i, định nghĩa số phức, khái niệm hai số phức bằng nhau, biểu diễn hình học của số phức, môđun của số phức, số phức liên hợp.
 + Khái niệm phép cộng, trừ, và nhân hai số phức.
 + Tổng và tích của hai số phức liên hợp, phép chia hai số phức.
 + Căn bậc hai của số thực âm, phương trình bậc hai với hệ số thực.
 - Kỹ năng: 
 + Biết khái niệm số i, định nghĩa số phức, khái niệm hai số phức bằng nhau. Biết cách biểu diễn hình học của số phức, Biết cách tính môđun của số phức, Biết cách tìm số phức liên hợp.
 + Biết khái niệm phép cộng, trừ, và nhân hai số phức. Biết cách tính cộng, trừ, và nhân hai số phức.
 + Biết cách tính tổng và tích hai số phức liên hợp, biết cách chia hai số phức.
 + Biết cách tính căn bậc hai của số thực âm, biết cách giải phương trình bậc hai với hệ số thực.
 - Thái độ: tích cực xây dựng bài,
 - Tư duy: hình thành tư duy logic, lập luận chặt chẽ, và linh hoạt trong quá trình suy nghĩ. 
II. Chuẩn bị 
	+ Giáo viên: Giáo án và các tài liệu liên quan
	+ Học sinh: Các kiến thức đã học về định nghĩa căn bậc hai của số phức và công thức nghiệm của phương trình bậc hai trên tập số phức..
III. Tiến trình bài dạy:
	1. Ổn định tổ chức(2 phút): Ổn định lớp, điểm danh
	2. Kiểm tra bài cũ(10 phút)
Câu hỏi 1: 
 Nêu công thức nghiệm của phương trình Az2 +Bz +C = 0 trên tập số phức ( với A, B, C là các số thực và A khác không). 
Áp dụng làm bài 10a) tr 144 giải pt sau trên tập số phức
Hoạt động của giáo viên
Hoạt động của HS
Ghi bảng
Hoạt động 1(10 phút): Biểu diễn hình học của số phức Z = a + bi 
(?)Mỗi số phức Z = a + bi biểu diễn ntn?
+) Nêu bài toán 5/ 143 (Sgk) . Yêu cầu lên bảng xác định ?
Hoạt động2(10phút)
giải bài tập 8
Chép đề,chia hs thành 3 nhóm cho hs thảo luận nhóm 
+) gọi hs nhóm khác nhận xét
+) Gv chốt lại kết quả
Hoạt động 3 (10phút)
giải bài tập 9
-Gọi 2 hs lên bảng trình bày bt đã chuẩn bị ở nhà
- Gọi hs nhận xét
- chốt lại nội dung kiến thức
+) Đại diện hs trả lời biểu diễn bởi một điểm M (a, b) trên mặt phảng tọa độ.
+) 1 hs lên bảng tbày lời giải đã chuẩn bị ở nhà
+mỗi nhóm cử một đại diện của nhóm học sinh làm bài trên bảng
+) Ad các qt cộng trừ, nhân ,chia hai số phức
+) Ad các qt cộng trừ, nhân ,chia hai số phức để tìm z
1/ Số phức Z có phần thực a = 1: Là đường thẳng qua hoành độ 1 và song song với Oy.
2/ Số phức Z có phần ảo b = -2: Là đường thẳng qua tung độ -2 và song song với Ox.
3/ Số phức Z có phần thực a ,phần ảo b : Là hình chữ nhật.
3/ : Là hình tròn có R = 2.
Bài 8 tr 143
Thực hiện các phép tính sau
a) (3+2i) [(2-i)+(3-2i) ]
b) 
c) 
Bài 9 tr 143
Giải các pt sau trên tập số phức
(3+4i)z+(1-3i)=2+5i
(4+7i)z-(5-2i)=6iz
4/Củng cố: (5 phút)
- Nhắc lại hệ thống các kiến thức cơ bản : ĐN số phức, số phức liên hợp- Giải phương trình bậc hai với hệ số thực.
- HS thực hiện trên 3 phiếu học tập.
5/ Dặn dò: - Nắm vững lý thuyết chương 4.
- Giải các bài tập còn lại của chương - Xem lại bài tập đã giải.
-Chuẩn bị tiết sau kiểm tra 1 tiết của chương 4
V/ Phụ lục: 
1) Phiếu học tập số 1: 
Câu 1: Số phức Z = a + bi thỏa điều kiện nào để có điểm biểu diễn M ở phần gạch chéo trong hình a, b, c.( hình 71 tr 143)
2) Phiếu học tập số 2:
Câu 2: Giải phương trình : Z4 – Z2 – 5 = 0.
3) Phiếu học tập số 3: 
Câu 3: Tìm hai số phức Z1, Z2 thỏa : Z1 + Z2 = 1 và Z1Z2 = 7 
Tiết 69
Kiểm tra 45’
Ngày soạn: 23/3/2009 
Ngày dạy:24/3/2009 
I. MỤC TIÊU:
Kiến thức: Kiểm tra mức độ:
Nắm dạng đại số của số phức, biết cách biểu diễn hình học của số phức.
Nắm công thức tính nghiệm của PT bậc 2 với hệ số phức.
các phép toán cộng, trừ, nhân, chia số phức.
 2. Tư duy, thái độ: Tập trung, độc lập, cẩn thận và sáng tạo trong kiểm tra.
II- Đề bài
Câu 1:
 Xác định phần thực và phần ảo và môđun của mỗi số phức sau:
 a) z1 = i – ( 2 – 3i ) – ( 2 + 4i )
 b) z2= 
Câu 2: Thực hiện phép tính: 
C âu 3: Giải phương trình sau trên C: z2+8z+17=0
Câu 4: Trên mặt phẳng Tìm tập hợp điểm biểu diễn các số phức thoả mãn
Phần thực thuộc đoạn [-2;3], phần ảo thuộc đoạn [0; 4]
Tiết 70- 71
 THỰC HÀNH GIẢI TOÁN TRÊN MÁY TÍNH CẦM TAY
Tiết 72 
ÔN TẬP CUỐI NĂM
øng dông ®¹o hµm ®Ó kh¶o s¸t vµ vÏ ®å thÞ cña hµm sè
Ngày soạn: 3/4/2009 
Ngày dạy:5/4/2009 
I. Mục tiêu:
- Học sinh nắm vững các khái niệm: sự đồng biến và nghịch biến, cực trị, giá trị lớn nhất và giá trị nhỏ nhất của hàm số; khái niệm tiệm cận của đồ thị hàm số.
- Học sinh nắm chắc đồng thời thành thạo các kĩ năng xét sự đồng biến và nghịch biến, tìm cực trị, tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số; kĩ năng tìm tiệm cận của đồ thị hàm số.
- Học sinh khảo sát và vẽ đồ thị một cách thành thạo các hàm số theo quy định chủa chương trình và giải quyết được một số bài toán liên quan.
II. Chuẩn bị 
	+ Giáo viên: Giáo án,tổng hợp kiến thức cơ bản, phân loại các dạng bt 
	+ Học sinh: Các kiến thức đã học 
III. Tiến trình bài dạy:
	1. Ổn định tổ chức(2 phút): Ổn định lớp, điểm danh
	2. Kiểm tra bài cũ(kết hợp trong quá trình ôn tập)
 3. Nội dung bài mới
Hoạt động của GV
Hoạt động của HS
Ghi bảng
Hoạt động1(15 phút)
GV nhắc lại nội dung kiến thức cơ bản
(?) Nêu các dạng toán cần luyện tập
Hoạt động2(15 phút)
Gọi 1hs lên bảng trình bày ý a)
Gọi hs khác nhận xét bổ sung
Chỉnh sửa nếu cần
Hoạt động3(8 phút)
Cho hs thảo luận theo nhóm ý b)
lắng nghe hồi tưởng kiến thức
+) Khảo sát vẽ đồ thị các hàm số dạng
Các bt về pttt...
+) Trình bày nội dung phần khảo sát
+) các hs khác cùng làm đối chiếu kết quả và nhận xét
+) Ghi nhớ
+) Thảo luận cử đại diện lên trình bày
1 C¸c kiÕn thøc c¬ b¶n cÇn nhí : 
(Xem chủ đề 1: sách hướng dẫn ôn tập thi tốt nghiệp THPT môn toán NXBGD năm học 08-09 trang 10)
2- C¸c d¹ng to¸n cÇn luyÖn tËp : theo sách ôn tập thi TN
3. Một số bài tập tổng hợp:
Bài 1: Cho hàm số .
a. Khảo sát và vẽ đồ thị hàm số khi m=1.
b. Xác định m để hàm số đồng biến trên tập R.
Bài 2: Cho hàm số (1)
a. Khảo sát sbt và vẽ đồ thị (C) hàm số khi m=1/3.
b. Biện luận theo m số cực trị của hàm số (1).
Bài 3 : Cho hàm số gọi (C) là đồ thị hàm số đã cho
a. Khảo sát sbt và vẽ đồ thị hàm số
b. Tìm các điểm trên (C) có tọa độ là những số nguyên
c. Chứng minh rằng đường thẳng D:y=2x+m luôn cắt đồ thị (C) tại hai điểm phân biệt MN ;xác định m để đoạn MN có độ dài nhỏ nhất 
IV- Củng cố dặn dò: (5 phút)
Với mỗi dạng hàm số 
,,
thường có các bài toán liên quan nào? pp giải bài toán đó?
Tiết 73
KIỂM TRA CUỐI NĂM
Theo đề chung của Sở 
Tiết 74=>78
TỔNG ÔN TẬP CHO THI TỐT NGHIỆP