Tài liệu ôn thi tốt nghiệp THPT môn Toán
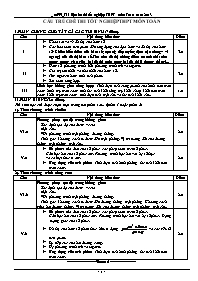
Nội dung kiến thức
Khảo sát và vẽ đồ thị của hàm số
Các bào toán liên quan đến ứng dụng của đạo hàm và đồ thị của hàm số: Chiều biến thiên của hàm số; cực trị; tiếp tuyến; tiệm cận (đứngv và ngang) của đồ thị hàm số. Tìm trên đồ thị những điểm có tính chất cho trước; tương giao giữa hai đồ thị (một trong hai đồ thị là đương thẳng).
Hàm số, phương trình, bất phương trình mũ và lôgarit.
Giá trị lớn nhất và nhỏ nhất của hàm số.
Tìm nguyên hàm, tính tích phân.
Bài toán tổng hợp.
Hình học không gian (tổng hợp): Tính diện tích xung quanh của hình nón tròn xoay, hình trụ tròn xoay; tính thể tích khối lăng trụ, khối chóp, khối nón tròn xoay, khối trụ tròn xoay; tính diện tích mặt cầu và thể tích khối cầu.
Bạn đang xem 20 trang mẫu của tài liệu "Tài liệu ôn thi tốt nghiệp THPT môn Toán", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
CẤU TRÚC ĐỀ THI TỐT NGHIỆP THPT MÔN TOÁN I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7 điểm). Câu Nội dung kiến thức Điểm I Khảo sát và vẽ đồ thị của hàm số Các bào toán liên quan đến ứng dụng của đạo hàm và đồ thị của hàm số: Chiều biến thiên của hàm số; cực trị; tiếp tuyến; tiệm cận (đứngv và ngang) của đồ thị hàm số. Tìm trên đồ thị những điểm có tính chất cho trước; tương giao giữa hai đồ thị (một trong hai đồ thị là đương thẳng)... 3.0 II Hàm số, phương trình, bất phương trình mũ và lôgarit. Giá trị lớn nhất và nhỏ nhất của hàm số. Tìm nguyên hàm, tính tích phân. Bài toán tổng hợp. 3.0 III Hình học không gian (tổng hợp): Tính diện tích xung quanh của hình nón tròn xoay, hình trụ tròn xoay; tính thể tích khối lăng trụ, khối chóp, khối nón tròn xoay, khối trụ tròn xoay; tính diện tích mặt cầu và thể tích khối cầu. 1.0 II. PHẦN RIÊNG (3.0 điểm). Thí sinh học chỉ được chọn một trong hai phần sau: (phần 1 hoặc phần 2) 1). Theo chương trình chuản: Câu Nội dung kiến thức Điểm VI.a Phương pháp tọa độ trong không gian: + Xác định tọa độ của điểm, vectơ + Mặt cầu. + Viết phương trình mặt phẳng, đường thẳng. + Tính góc; khoảng cách từ điểm đến mặt phẳng. Vị trí tương đối của đường thẳng, mặt phẳng, mặt cầu. 2.0 V.a Số phức: Mô đun của số phức, các phép toán trên số phức. Căn bậc hai của số phức âm. Phương trình bậc hai với hệ số thực và có biệt thức Δ âm. Ứng dụng của tích phân: Tính diện tích hình phẳng, thể tích khối nón tròn xoay. 2.0 2). Theo chương trình nâng cao: Câu Nội dung kiến thức Điểm VI.b Phương pháp tọa độ trong không gian: + Xác định tọa độ của điểm, vectơ + Mặt cầu. + Viết phương trình mặt phẳng, đường thẳng. + Tính góc; khoảng cách từ điểm đến đường thẳng, mặt phẳng; Khoảng cách giữa hai đường thẳng. Vị trí tương đối của đường thẳng, mặt phẳng, mặt cầu. 2.0 V.b Số phức: Mô đun của số phức, các phép toán trên số phức. Căn bậc hai của số phức âm. Phương trình bậc hai với hệ số phức. Dạng lượng giác của số phức. Đồ thị của hàm số phân thức hữu tỉ dạng: và các yếu tố liên quan. Sự tiếp xúc của hai đường cong. Hệ phương trình mũ và lôgarit. Ứng dụng của tích phân: Tính diện tích hình phẳng, thể tích khối nón tròn xoay. 2.0 -----------------The end----------------- MỘT SỐ KIẾN THỨC CƠ BẢN VỀ LƯỢNG GIÁC I. BẢNG GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT SỐ CUNG (GÓC) ĐẶC BIỆT: Cung/góc GTLG sin cos tan cot II. CÔNG THỨC LƯỢNG GIÁC: 1. Công thức cộng: 2. Công thức nhân đôi: 3. Công thức hạ bậc: 4. Công thức biến đổi tích thành tổng: 6. Các hằng đẳng thức lượng giác: 5 Công thức biến đổi tổng thành tích: III. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN: Phương trình Phương trình Phương trình Phương trình IV. PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP: 1. Phương trình dạng: asinx + bcosx = c. ; Trong đó: 2. Phương trình dạng: asin2x + bsinx.cosx + ccos2x = d. Phương pháp: + Kiểm tra với cos x = 0 có phải là nghiệm của phương trình không? + Nếu , chia 2 vế của phương trình cho cos2x , ta được: atan2x + btanx + c = d(1 + tan2x) IV. MỘT SỐ CÔNG THỨC HAY DÙNG: BẢNG ĐẠO HÀM PHẦN GIẢI TÍCH Chương I: KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ I. KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ BẬC 3; BẬC 4. 1. Các bước khảo sát hàm số: + Tập xác định: . + Tính đạo hàm , giải phương trình và tìm các điểm cực trị của hàm số. + Tính các giới hạn . + Lập bảng biến thiên, nhận xét về tính đơn điệu và cực trị của đồ thị hàm số. + Vẽ đồ thị: ( Tìm các điểm đặc biệt, tâm đối xứng của đồ thị, các giao điểm với truc Ox, trục Oy) 2. Các dạng đồ thị: Hàm số bậc 3 Hàm số bậc 4 Có điểm cực đại và cực tiểu Có điểm cực đại và cực tiểu O y x O y x y x O y x O Không có cực trị Không có cực trị y x O y x O y x O y x O 3. Các ví dụ: Hàm số bậc 3 Hàm số bậc 4 Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số: . Giải * Tập xác định: . * Đạo hàm: . * Cho * Giới hạn: * Bảng biến thiên: x – 2 0 y’ + 0 – 0 + 0 y – 4 * Nhận xét: + Hàm số đồng biến trên và , nghịch biến trên . + Hàm số đạt cực đại tại: . + Hàm số đạt cực tiểu tại: . *Đồ thị: + Đồ thị nhận điểm làm tâm đối xứng. + Cho . + Cho . Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số: . Giải * Tập xác định: . * Đạo hàm: . * Cho * Giới hạn: * Bảng biến thiên: x – 1 0 1 y’ – 0 + 0 – 0 + – 3 y – 4 – 4 * Nhận xét: + Hàm số đồng biến trên và , nghịch biến trên và . + Hàm số đạt cực đại tại: . + Hàm số đạt cực tiểu tại: . *Đồ thị: + Cho . + Cho . II. KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM PHÂN THỨC Các bước khảo sát Ví dụ * Tập xác định: . * Tính đạo hàm: . * Giới hạn; các đường tiệm cận: Tiệm cận đứng: Tiệm cận ngang: . * Bảng biến thiên: +TH: x y’ + + y +TH: x y’ – – y * Đồ thị: + Tìm các điểm đặc biệt với trục Ox, Oy. Ä: Chú ý: + Đồ thị nhận điểm làm tâm đối xứng. Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: . Giải * Tập xác định: . * Tính đạo hàm: . * Giới hạn; các đường tiệm cận: +Ta có: Tiệm cận đứng: + Tiệm cận ngang: . * Bảng biến thiên: x y’ – – y * Nhận xét: + Hàm số luôn nghịch biến trên các khoảng . + Hàm số không có cực trị. * Đồ thị: + Cho + Cho BÀI TẬP Bài tập 1. Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: 1. 5. 9. 2. 6. 10. 3. 7. 11. 4. 8. 12. Bài tập 2. Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: 1. 4. 7. 2. 5. 8. 3. 6. Bài tập 3. Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: 1. 4. 7. 10. 2. 5. 8. 11. 3. 6. 9. 12. 13. ------------------------------------ CÁC BÀI TOÁN LIÊN QUAN ĐÉN KHẢO SÁT HÀM SỐ BÀI TOÁN 1: Xét tính đồng biến, nghịch biến của hàm số. Phương pháp Ví dụ + Tìm tập xác định. + Tính đạo hàm . Tìm các điểm ( i = 1,,n) mà tại đó đạo hàm bằng 0 hoặc không xác định. + Sắp xếp các điểm theo thứ tự tăng dần và lập bảng biến thiên. + Nêu kết luận về các khoảng đồng biến nghịch biến ( Hàm số đồng biến trên khoảng mà và ngược lại) Ví dụ: Xét sự đồng biến, nghịch biến của hàm số: . Giải * Tập xác định: . * Đạo hàm: . * Bảng biến thiên: x – 1 2 y’ + 0 – 0 + y * Kết luận: + Hàm số đồng biến trên các khoảng và và nghịch biến trên . Bài tập: Xét tính đồng biến, nghịch biến của hàm số: (TN THPT 2007 – lần 2). BÀI TOÁN 2: Định giá trị của m để hàm số đồng biến, nghịch biến trên tập xác định . 1. Định lí về dấu của tam thức bậc 2: Cho tam thức bậc 2: có . Khi đó: Nếu thì f(x) cùng dấu với hệ số a với mọi . Nếu thì f(x) cùng dấu với hệ số a với mọi trừ tại . Nếu , giả sử f(x) có 2 nghiệm ta có bảng xét dấu: x f(x) cùng dấu a 0 trái dấu a 0 cùng dấu a 2. Định giá trị của m: Đối với hàm bậc 3 Đối với hàm nhất biến: + Tập xác định: . + Đạo hàm: +TXĐ: .Đạo hàm:. + y đồng biến trên D + y nghịch biến trên D + y đồng biến trên từng khoảng D + y nghịch biến trên từng khoảng D Ví dụ: Định m để hàm số: đồng biến trên tập xác định. Giải * Tập xác định: . * Đạo hàm: Ta có: * Để hàm số đồng biến trên tập xác định thì: Ví dụ: Định m để hàm số: . đồng biến trên tập xác định. Giải * Tập xác định: . * Ta có: . * Để hàm số đồng biến trên tập xác định thì: BÀI TẬP 1. Cho hàm số: . Định m để hàm số (1) đồng biến trên tập xác định của nó. 2. Cho hàm số: . Định m để hàm số (1) đồng biến trên tập xác định của nó. 3. Cho hàm số: . Định m để hàm số (1) đồng biến trên tập xác định của nó. BÀI TOÁN 3: Tìm GTLN, GTNN của hàm số trên đoạn [a;b] . Cho hàm số xác định trên đoạn Phương pháp Ví dụ * Tính đạo hàm * Giải pt: , tìm các nghiệm . * Tính các giá trị * Tìm số lớn nhất M và số nhỏ nhất m trong các số ở trên. Khi đó: Ví dụ: Tìm GTLN, GTNN của hàm số: trên đoạn Giải * Đạo hàm: * Cho * Ta có: * Vậy: đạt được tại đạt được tại BÀI TẬP 1. Tìm GTLN, GTNN của hàm số trên đoạn (TN THPT 2007) 2. Tìm GTLN, GTNN của hàm số trên đoạn (TN THPT 2008 – lần 1) 3. Tìm GTLN, GTNN của hàm số trên đoạn (TN THPT 2008 – lần 2) 4. Tìm GTLN, GTNN của hàm số trên đoạn 5. Tìm GTLN, GTNN của hàm số trên đoạn (TN THPT 2009) 6. Tìm GTLN, GTNN của hàm số trên đoạn 7. Tìm GTLN, GTNN của hàm số trên đoạn BÀI TOÁN 4: Phương trình tiếp tuyến của đồ thị hàm số. Phương trình tiếp tuyến (PTTT) của đồ thị hàm số có đồ thị (C) tại điểm và có hệ số góc là: Các dạng toán thường gặp: Lập phương trình tiếp tuyến với đồ thị của ham số (C). 1). Tại điểm có hoành độ ( tung độ ) cho trước. * Cách giải: + Thay vào đồ thị (C) và rút ra + Thay vào đồ thị (C) và rút ra * Lưu ý: + Tại giao điểm của đồ thị (C) với trục tung. Ta có: + Tại giao điểm của đồ thị (C) với trục hoành. Ta có: 2). Có hệ số góc k cho trước: * Phương pháp: Giải pt: tìm nghiệm từ đó rút ra . 3). Biết tiếp tuyến đó song song với đường thẳng (d): . * Phương pháp: Vì tiếp tuyến // d, từ pt: ta tìm , rồi thay vào đồ thị của hàm số để rút ra . 4). Biết tiếp tuyến đó vuông góc với đường thẳng (d): . * Phương pháp: Vì tiếp tuyến vuông góc với d nên , từ pt: ta tìm , rồi thay vào đồ thị của hàm số để rút ra . Ví dụ 1:Cho hàm số, gọi đồ thị của hàm số là (C). Viết phương trình tiếp tuyến với đồ thị (C). 1. Tại điểm có hoành độ bằng –1. 2. Tại điểm có tung độ bằng 2. 3. Tại giao điẻm của đồ thị với trục hoành. 4. Tại giao điẻm của đồ thị với trục tung. Giải Ta có: . 1. Theo y/cầu b.toán, ta có: . Hệ số góc: Vậy phương trình tiếp tuyến cần tìm là: hay . 2. Theo y/cầu bài toán, ta có: . Hệ số góc: Vậy phương trình tiếp tuyến cần tìm là: hay . 3. Theo y/cầu bài toán, ta có: . Hệ số góc: Vậy phương trình tiếp tuyến cần tìm là: hay . 4. Theo y/cầu b.toán, ta có: . Hệ số góc: Vậy phương trình tiếp tuyến cần tìm là: hay . Ví dụ 2: Cho hàm số, gọi đồ thị của hàm số là (C). Viết phương trình tiếp tuyến với đồ thị (C). 1. Tại điểm có hệ số góc bằng –2. 2. Biết tiếp tuyến đó song song với đường thẳng (d): . 3. Biết tiếp tuyến đó vuông góc với đường thẳng (d): . Giải * Ta có: . 1. Theo yêu cầu bài toán, ta có: + Với . Suy ra PTTT cần tìm là: hay + Với . Suy ra PTTT cần tìm là: hay 2. Vì tiếp tuyến đó song song với đường thẳng (d): nên hệ số góc: Ta có: + Với . Suy ra PTTT cần tìm là: hay + Với . Suy ra PTTT cần tìm là: hay 3. Vì tiếp tuyến đó vuông góc với đường thẳng (d): nên hệ số góc: Ta có: + Với . Suy ra PTTT cần tìm là: hay + Với . Suy ra PTTT cần tìm là: hay BÀI TẬP Viết PTTT với đồ thị hàm số tại điểm có hoành độ (TN THPT 2006). Cho hàm số có đồ thị (C).Viết PTTT với (C) tại điểm cực đại (TN THPT 2007). Cho HS có đồ thị (C).Viết PTTT với (C) tại điểm có tung độ bằng –2 (TN THPT 2008). Cho HS có đồ thị (C). Viết PTTT với (C), biết hệ số góc của tiếp tuyến bằng –5 (TN THPT 2009). Cho HS có đồ thị (C).Viết PTTT với (C) tại điểm hoành độ bằng 2. Cho HS có đồ thị (C). Viết PTTT với (C), biết tiếp tuyến đó song song voái đường thẳng . BÀI TOÁN 5: Dùng đồ thị (C): y = f(x) biện luận theo m số nghiệm của phương trình f(x;m) =0 . * Phương pháp: + Biến đôi và đưa phương trình về dạng: (1). + Đặ ... BC). Viết phương trình tiếp diện với mặt cầu (S) song song với mp(ABC). Va (1,0 điểm): Giải phương trình sau đây trên tập số phức: 2. Theo chương trình nâng cao: IVb (2,0 điểm): Trong không gian Oxyz, cho đường thẳng d và mặt phẳng (P) lần lượt có phương trình: 1) Tìm tọa độ giao điểm của đường thẳng d và mp(P). 2) Tính góc giữa đường thẳng d và mặt phẳng (P). 3) Viết phương trình hình chiếu vuông góc của đường thẳng d lên mặt phẳng (P). Vb (1,0 điểm): Giải hệ phương trình: -----------------------Hết----------------------- ĐỀ THI THỬ TỐT NGHIỆP KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2013 ĐỀ SỐ 15 Môn thi: TOÁN – Giáo dục trung học phổ thông Thời gian bài làm: 150 phút, không kể thời gian giao đề. ------------------------- --------------------------------------------- I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm) Câu I (3,0 điểm): Cho hàm số 1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số . 2) Viết phương trình tiếp tuyến của (C) tại điểm trên (C) có hoành độ , với . 3) Tìm tham số m để phương trình: có đúng 2 nghiệm phân biệt. Câu II (3,0 điểm): 1) Giải phương trình: 2) Tính tích phân: 3) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: trên đoạn Câu III (1,0 điểm): Cho hình lăng trụ đứng , có đáy ABC là tam giác vuông tại B, BC = a, mặt tạo với đáy một góc 300 và tam giác có diện tích bằng . Tính thể tích của khối lăng trụ. II. PHẦN RIÊNG (3,0 điểm). Thí sinh chỉ được chọn một trong hai phần dưới đây. 1. Theo chương trình chuẩn: IVa (2,0 điểm): Trong không gian với hệ tọa độ Oxyz, cho hai điểm và mặt phẳng (P) : 1) Viết phương trình tham số của đường thẳng AB. Chứng minh rằng: . 2) Viết phương trình mặt cầu (S) có đường kính là AB. 3) Chứng minh (P) là tiếp diện của mặt cầu (S) . Tìm tọa độ tiếp điểm của (P) và (S). Va (1,0 điểm): Cho số phức . Tìm số nghịch đảo của số phức: 2. Theo chương trình nâng cao: IVb (2,0 điểm): Trong không gian với hệ tọa độ Oxyz, cho điểm và đường thẳng có phương trình: 1) Viết phương trình mặt phẳng (P) đi qua điểm I và chứa đường thẳng . 2) Tính khoảng cách từ điểm I đến đường thẳng . 3) Viết phương trình mặt cầu (S) có tâm là điểm I và cắt đường thẳng tại hai điểm phân biệt A và B sao cho đoạn AB có độ dài bằng 4. Vb (1,0 điểm): Gọi là hai nghiệm của phương trình: . Hãy lập một phương trình bậc hai nhận làm nghiệm. -----------------------Hết----------------------- ĐỀ THI THỬ TỐT NGHIỆP KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2013 ĐỀ SỐ 16 Môn thi: TOÁN – Giáo dục trung học phổ thông Thời gian bài làm: 150 phút, không kể thời gian giao đề. ------------------------- --------------------------------------------- I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm) Câu I (3,0 điểm): Cho hàm số 1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số . 2) Dùng đồ thị (C), hãy biện luận số nghiệm của phương trình: 3) Tính diện tích hình phẳng giới hạn bởi đồ thị (C) và trục hoành. Câu II (3,0 điểm): 1) Giải phương trình: 2) Tính tích phân: 3) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: Câu III (1,0 điểm): Cho hình chóp S.ABC có BC = 2a, đáy ABC là tam giác vuông tại C, SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi I là trung điểm của đoạn AB. 1) Chứng minh rằng 2) Biết mặt bên (SAC) hợp với mặt đáy (ABC) một góc 600 .Tính thể tích của khối chóp S.ABC. II. PHẦN RIÊNG (3,0 điểm). Thí sinh chỉ được chọn một trong hai phần dưới đây. 1. Theo chương trình chuẩn: IVa (2,0 điểm): Trong không gian với hệ tọa độ Oxyz, cho hai điểm và mặt phẳng (P) : 1) Viết phương trình đường thẳng AB và phương trình mặt cầu đường kính AB. 2) Viết phương trình mặt phẳng (Q) chứa hai điểm A, B đồng thời vuông góc với mặt phẳng (P). Va (1,0 điểm): Giải phương trình trên sau tập số phức: 2. Theo chương trình nâng cao: IVb (2,0 điểm): Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng 1) Viết phương trình mặt cầu (S) tâm tiếp xúc với (Q). Tìm tọa độ tiếp điểm. 2) Viết phương trình mặt phẳng (P) đi qua hai điểm , đồng thời tạo với mặt cầu (S) một đường tròn có bán kính bằng 2. Vb (1,0 điểm): Trên mặt phẳng phức, tìm tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện: -----------------------Hết----------------------- ĐỀ THI THỬ TỐT NGHIỆP KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2013 ĐỀ SỐ 17 Môn thi: TOÁN – Giáo dục trung học phổ thông Thời gian bài làm: 150 phút, không kể thời gian giao đề. ------------------------- --------------------------------------------- I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm) Câu I (3,0 điểm): Cho hàm số 1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số . 2) Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành. 3) Tìm tham số m để phương trình: có nghiệm duy nhất. Câu II (3,0 điểm): 1) Giải phương trình: 2) Tính tích phân: 3) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: trên đoạn Câu III (1,0 điểm): Cho khối chóp S.ABC có ABC và SBC là hai tam giác đều có cạnh bằng 2, . Tính thể tích của khối chóp S.ABC theo a. II. PHẦN RIÊNG (3,0 điểm). Thí sinh chỉ được chọn một trong hai phần dưới đây. 1. Theo chương trình chuẩn: IVa (2,0 điểm): Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có tọa độ các đỉnh: 1) Chứng minh ABC là tam giác vuông. Xác đinh tọa độ đỉnh D để bốn điểm A,B,C.D là bốn đỉnh của một hình chữ nhật. 2) Gọi M là điểm thỏa mãn . Viết phương trình mặt phẳng (P) đi qua điểm M và vuông góc với đường thẳng BC. Viết phương trình mặt cầu tâm A, tiếp xúc với mp(P). Va (1,0 điểm): Tính diện tích hình phẳng giới hạn bởi các đường sau đây: 2. Theo chương trình nâng cao: IVb (2,0 điểm): Trong không gian với hệ tọa độ Oxyz, cho điểm và đường thẳng : 1) Tìm tọa độ hình chiếu vuông góc của điểm M lên đường thẳng d. Viết phương trình mặt cầu tâm M, tiếp xúc với đường thẳng d. 2) Viết phương trình mặt phẳng (P) đi qua điểm M, song song với d và cách d một khoảng bằng 4. Vb (1,0 điểm): Cho số phức: . Hãy viết dạng lượng giác của số phức . -----------------------Hết----------------------- ĐỀ THI THỬ TỐT NGHIỆP KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2013 ĐỀ SỐ 18 Môn thi: TOÁN – Giáo dục trung học phổ thông Thời gian bài làm: 150 phút, không kể thời gian giao đề. ------------------------- --------------------------------------------- I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm) Câu I (3,0 điểm): Cho hàm số 1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số . 2) Viết phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng . 3) Tìm các giá trị của k để (C) và cắt nhau tại 2 điểm phân biệt. Câu II (3,0 điểm): 1) Giải phương trình: 2) Tính tích phân: 3) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: trên đoạn Câu III (1,0 điểm): Cho một hình trụ có độ dài trục . ABCD là hình vuông cạnh bằng 8 có các đỉnh nằm trên hai đường tròn đáy sao cho tâm của hình vuông là trung điểm của đoạn . Tính thể tích của hình trụ đó. II. PHẦN RIÊNG (3,0 điểm). Thí sinh chỉ được chọn một trong hai phần dưới đây. 1. Theo chương trình chuẩn: IVa (2,0 điểm): Trong không gian Oxyz, cho đường thẳng và mặt phẳng lần lượt có phương trình: 1) Chứng minh rằng đường thẳng song song với mặt phẳng . Tính khoảng cách từ đường thẳng đến mặt phẳng . 2) Tìm tọa độ giao điểm A của đường thẳng với mặt phẳng (Oxy). Viết phương trình mặt cầu tâm A, tiếp xúc với mp Va (1,0 điểm): Cho . Tính mô đun của số phức . 2. Theo chương trình nâng cao: IVb (2,0 điểm): Trong không gian với hệ tọa độ Oxyz, cho điểm , mặt phẳng : và hai đường thẳng : 1) Tìm tọa độ điểm đối xứng với điểm qua đường thẳng . 2) Viết phương trình đường thẳng cắt cả hai đường thẳng và nằm trong mp(P). Vb (1,0 điểm): Giải phương trình sau trên tập số phức: -----------------------Hết----------------------- ĐỀ THI THỬ TỐT NGHIỆP KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2013 ĐỀ SỐ 19 Môn thi: TOÁN – Giáo dục trung học phổ thông Thời gian bài làm: 150 phút, không kể thời gian giao đề. ------------------------- --------------------------------------------- I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm) Câu I (3,0 điểm): Cho hàm số 1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số . 2) Viết phương trình tiếp tuyến của (C) tại điểm cực tiểu của nó. 3) Tìm giá trị của tham số m để phương trình sau đây có 4 nghiệm phân biệt: Câu II (3,0 điểm): 1) Giải phương trình: 2) Tính tích phân: 3) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:. Câu III (1,0 điểm): Cho hình lăng trụ đứng , có đáy ABC là tam giác vuông tại A, AC = a, . Đường chéo tạo với mặt bên tạo với mặt phẳng một góc . Tính thể tích của khối lăng trụ theo a. II. PHẦN RIÊNG (3,0 điểm). Thí sinh chỉ được chọn một trong hai phần dưới đây. 1. Theo chương trình chuẩn: IVa (2,0 điểm): Trong không gian với hệ tọa độ Oxyz, cho điểm và mặt phẳng (P) có phương trình: 1) Tìm tọa độ hình chiếu của điểm A lên mặt phẳng (P). 2) Viết phương trình mặt cầu tâm A và đi qua gốc tọa độ. Va (1,0 điểm): Cho số phức thỏa mãn: . Tìm phần thực, phần ảo và tính mô đun của số phức z. 2. Theo chương trình nâng cao: IVb (2,0 điểm): Trong không gian với hệ tọa độ Oxyz, cho điểm và đường thẳng có phương trình: 1) Tìm tọa độ hình chiếu của điểm A lên đường thẳng d. 2) Viết phương trình mặt cầu tâm A và tiếp xúc với đường thẳng d.. Vb (1,0 điểm): Cho hàm số . Tìm trên (C) các điểm cách đều hai trục tọa độ. -----------------------Hết----------------------- ĐỀ THI THỬ TỐT NGHIỆP KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2013 ĐỀ SỐ 20 Môn thi: TOÁN – Giáo dục trung học phổ thông Thời gian bài làm: 150 phút, không kể thời gian giao đề. ------------------------- --------------------------------------------- I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm) Câu I (3,0 điểm): Cho hàm số 1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số . 2) Tìm giá trị của tham số m để phương trình sau đây có 3 nghiệm phân biệt: Câu II (3,0 điểm): 1) Giải phương trình: 2) Tính tích phân: 3) Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điẻm của nó với đường thẳng Câu III (1,0 điểm): Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. 1) Tính diện tích xung quanh và diện tích toàn phần của hình nón. 2) Tính diện tích của khối nón tương ứng. II. PHẦN RIÊNG (3,0 điểm). Thí sinh chỉ được chọn một trong hai phần dưới đây. 1. Theo chương trình chuẩn: IVa (2,0 điểm): Trong không gian với hệ tọa độ , cho hình hộp có 1) Viết phương trình mặt phẳng và tính khoảng cách từ đến . 2) Tìm tọa độ đỉnh C và viết phương trình cạnh CD của hình hộp Va (1,0 điểm): Cho . Tính . 2. Theo chương trình nâng cao: IVb (2,0 điểm): Trong không gian với hệ tọa độ , cho hình hộp có 1) Tìm tọa độ các đỉnh C,D và chứng minh rằng: là hình hộp chữ nhật. 2) Viết phương trình mặt cầu ngoại tiếp hình hộp . Vb (1,0 điểm): Cho . Tính . -----------------------Hết----------------------- Chúc các em thi tốt nghiệp đạt kết quả cao !
Tài liệu đính kèm:
 12.doc
12.doc





