Tài liệu ôn tập môn Toán THPT- Giáo dục trung học Tây Ninh

TÀI LIỆU ÔN THI TỐT NGHIỆP
TRUNG HỌC PHỔ THÔNG MÔN TOÁN
HÌNH HỌC KHÔNG GIAN TỔNG HỢP
·PHẦN 1. TÓM TẮT LÝ THUYẾT: 
	A.QUAN HỆ SONG SONG
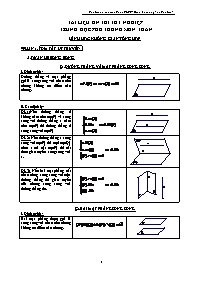
§1.ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG 
I. Định nghĩa:
Đường thẳng và mặt phẳng gọi là song song với nhau nếu chúng không có điểm nào chung.
II.Các định lý:
ĐL1:Nếu đường thẳng d không nằm trên mp(P) và song song với đường thẳng a nằm trên mp(P) thì đường thẳng d song song với mp(P)
ĐL2: Nếu đường thẳng a song song với mp(P) thì mọi mp(Q) chứa a mà cắt mp(P) thì cắt theo giao tuyến song song với a.
ĐL3: Nếu hai mặt phẳng cắt nhau cùng song song với một đường thẳng thì giao tuyến của chúng song song với đường thẳng đó.
§2.HAI MẶT PHẲNG SONG SONG
I. Định nghĩa:
Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm nào chung.
II.Các định lý:
ĐL1: Nếu mp(P) chứa hai đường thẳng a, b cắt nhau và cùng song song với mặt phẳng (Q) thì (P) và (Q) song song với nhau.
ĐL2: Nếu một đường thẳng nằm một trong hai mặt phẳng song song thì song song với mặt phẳng kia.
ĐL3: Nếu hai mặt phẳng (P) và (Q) song song thì mọi mặt phẳng (R) đã cắt (P) thì phải cắt (Q) và các giao tuyến của chúng song song.
B.QUAN HỆ VUÔNG GÓC
§1.ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG
I.Định nghĩa:
Một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trên mặt phẳng đó.
II. Các định lý:
ĐL1: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mp(P) thì đường thẳng d vuông góc với mp(P).
ĐL2: (Ba đường vuông góc) Cho đường thẳng a không vuông góc với mp(P) và đường thẳng b nằm trong (P). Khi đó, điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a’ của a trên (P).
§2.HAI MẶT PHẲNG VUÔNG GÓC
I.Định nghĩa:
Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 900.
II. Các định lý:
ĐL1:Nếu một mặt phẳng chứa một đường thẳng vuông góc với một mặt phẳng khác thì hai mặt phẳng đó vuông góc với nhau.
ĐL2:Nếu hai mặt phẳng (P) và (Q) vuông góc với nhau thì bất cứ đường thẳng a nào nằm trong (P), vuông góc với giao tuyến của (P) và (Q) đều vuông góc với mặt phẳng (Q). 
ĐL3: Nếu hai mặt phẳng (P) và (Q) vuông góc với nhau và A là một điểm trong (P) thì đường thẳng a đi qua điểm A và vuông góc với (Q) sẽ nằm trong (P)
ĐL4: Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.
§3.KHOẢNG CÁCH
1. Khoảng cách từ 1 điểm tới 1 đường thẳng , đến 1 mặt phẳng: Khoảng cách từ điểm M đến đường thẳng a (hoặc đến mặt phẳng (P)) là khoảng cáchgiữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên đường thẳng a ( hoặc trên mp(P))
d(O; a) = OH; d(O; (P)) = OH
2. Khoảng cách giữa đường thẳng và mặt phẳng song song: Khoảng cách giữa đường thẳng a và mp(P) song song với a là khoảng cách từ một điểm nào đó của a đến mp(P).
d(a;(P)) = OH
3. Khoảng cách giữa hai mặt phẳng song song: là khoảng cách từ một điểm bất kỳ trên mặt phẳng này đến mặt phẳng kia.
d((P);(Q)) = OH
4.Khoảng cách giữa hai đường thẳng chéo nhau: là độ dài đoạn vuông góc chung của hai đường thẳng đó.
d(a;b) = AB
§4.GÓC
1. Góc giữa hai đường thẳng a và b là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt cùng phương với a và b. 
2. Góc giữa đường thẳng a không vuông góc với mặt phẳng (P) là góc giữa a và hình chiếu a’ của nó trên mp(P).
Đặc biệt: Nếu a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa đường thẳng a và mp(P) là 900.
3. Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
4. Diện tích hình chiếu: Gọi S là diện tích của đa giác (H) trong mp(P) và S’ là diện tích hình chiếu (H’) của (H) trên mp(P’) thì 
, trong đó là góc giữa hai mặt phẳng (P),(P’).
	C. THỂ TÍCH CỦA KHỐI ĐA DIỆN:
1. THỂ TÍCH KHỐI LĂNG TRỤ:
V=Bh với 
	a) Thể tích khối hộp chữ nhật:
V=abc với a, b, c là ba kích thước
	b) Thể tích khối lập phương:
V=a3 với a là độ dài cạnh
2. THỂ TÍCH KHỐI CHÓP:
V=Bh với 
3. TỈ SỐ THỂ TÍCH TỨ DIỆN:
Cho khối tứ diện SABC và A’, B’, C’ là các điểm tùy ý lần lượt thuộc SA, SB, SC ta có:
3. THỂ TÍCH KHỐI CHÓP CỤT:
 với 
	D. DIỆN TÍCH HÌNH TRÒN XOAY- THỂ TÍCH KHỐI TRÒN XOAY:
1. Hình trụ- Khối trụ:
2. Hình nón – Khối nón	
3.Hình nón cụt – Khối nón cụt:
4. Mặt cầu – Khối cầu:
·PHẦN 2: CÁC VÍ DỤ
	Ví dụ 1: Cho khối chóp tứ giác đều S.ABCD có AB = a, góc giữa mặt bên và mặt đáy bằng 600. Tính thể tích của khối chóp S.ABCD theo a.
	Đáp án và biểu điểm:(1đ)
Ta có S.ABCD là khối chóp đều và AB = a nên đáy là hình vuông cạnh a, suy ra diện tích đáy là S = a2.
0,25đ
Gọi O là tâm của hình vuông và I là trung điểm của cạnh BC, ta có là góc giữa mặt bên và mặt đáy của khối chóp đã cho.
0,25đ
Trong tam giác vuông SOI, ta có:
0,25đ
Thể tích của khối chóp là:
0,25đ
	Ví dụ 2:Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = SB = a, mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD). Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
	Đáp án và biểu điểm(1đ)
Từ giả thiết ta có SAB là tam giác đều cạnh a. Gọi G và I lần lượt là tâm của tam giác đều SAB và tâm của hình vuông ABCD. Gọi O là tâm của mặt cầu ngoại tiếp hình chóp ta có OG^(SAB), OI ^(ABCD)
0,5đ
Từ đó ta suy ra tứ giác OIGH là một hình chữ nhật ( với H là trung điểm của BC) nên OG = IH = 
0,25đ
Ký hiệu R là bán kính của mặt cầu ngoại tiếp hình chóp. Trong DOGA vuông tại G ta có:
0,25đ
	Ví dụ 3: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A với AB = a, AC = a, mặt bên SBC là tam giác đều và vuông góc với mặt phẳng đáy. Tính theo a thể tích của khối chóp S.ABC.
	Đáp án và biểu điểm:(1đ)
Gọi H là trung điểm của BC. Do DSBC đều nên SH ^ BC. Mà (SBC) ^ (ABC) nên SH^(ABC) Þ SH là đường cao của hình chóp S.ABC.
0,25đ
Diện tích đáy của hình chóp là 
0,25đ
Ta có DABC vuông tại A nên 
Hơn nũa DSBC đều Þ SH= 
0,25đ
Thể tích của khối chóp là:
0,25đ
	Ví dụ 4: Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’= b và đường thẳng AA’ tạo với mặt phẳng (ABC) một góc 600. Tính thể tích khối tứ diện ACA’B’ theo a và b.
	Đáp án và biểu điểm(1đ)
Ký hiệu h và V tương ứng là chiều cao và thể tích của khối lăng trụ đã cho, ta có:
0,25đ
Gọi H là hình chiếu vuông góc của A’ trên (ABC), ta có A’H = h và do đó 
0,25đ
Thể tích khối lăng trụ là 
0,25đ
Vậy thể tích khối tứ diện cần tìm là 
0,25đ
·PHẦN 3: CÁC BÀI TẬP ÔN LUYỆN
1) Tính thể tích khối tứ diện đều cạnh a.(ĐS: )
2) Cho khối chóp tứ giác đều S.ABCD biết AB = a và góc giữa mặt bên và mặt đáy bằng a. Tính thể tích khối chóp.(ĐS:)
3) Cho khối chóp tam giác đều S.ABC biết AB = a và SA = b. Tính thể tích khối chóp.(ĐS:)
4) Hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là một tam giác vuông tại A, AC = a =600. Đường chéo BC’ của mặt bên BB’C’C tạo với mp(AA’C’C) một góc 300. 
	a) Tính độ dài đoạn AC’.(ĐS: 3a)
	b) Tính thể tích của khối lăng trụ.(ĐS:)
5) Hình chóp cụt tam giác đều có cạnh đáy lớn 2a, đáy nhỏ là a, góc của đường cao với mặt bên là 300. 
	a) Tính diện tích toàn phần của hình chóp cụt.(ĐS:)
	b) Tính thể tích của khối chóp cụt.(ĐS: )
6) Một hình trụ có bán kính đáy R và thiết diện qua trục là một hình vuông.
	a) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ tương ứng.(ĐS: )
	b) Tính thể tích của khối lăng trụ tứ giác đều nội tiếp hình trụ đã cho.(ĐS: 4R3)
7) Cho hình chóp tứ giác đều có cạnh đáy là a, cạnh bên hợp với mặt đáy một góc 600. 
	a) Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp.
	b) Tìm bán kính của mặt cầu ngoại tiếp hình chóp. (ĐS:)
8) Một khối lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, cạnh bên BB’ = a, chân đường vuông góc hạ từ B’ xuống đáy ABC trùng với trung điểm I của cạnh AC.
	a) Tính góc giữa cạnh bên và mặt đáy.(ĐS: 300)
	b) Tính thể tích của khối lăng trụ.(ĐS: )
	c) Chứng minh mặt bên AA’C’C là hình chữ nhật.
9) Cho khối lăng trụ đứng ABC.A’B’C’ đáy là tam giác ABC vuông tại B. Biết BB’=AB=h và góc của B’C làm với mặt đáy bằng a.
	a) Chứng minh rằng .
	b) Tính thể tích của khối lăng trụ.(ĐS:)
	c) Tính diện tích thiết diện tạo nên do mặt phẳng ACB’ cắt khối lăng trụ.(ĐS: )
10) Cho tam giác đều ABC cạnh a nội tiếp trong đường tròn đường kính AD; SD là đoạn thẳng có độ dài a và vuông góc với mặt phẳng (ABC).
	a) Chứng minh SAC và SAB là những tam giác vuông.
	b) Tính diện tích toàn phần của hình chóp S.ABDC.(ĐS: )
	c) Tìm một điểm cách đều 5 điểm A, B, C, D, S.
11) Cho khối chóp S.ABCD có đáy ABCD là hình vuông và hai mặt bên SAB và SAD cùng vuông góc với đáy, góc của cạnh SC với mặt bên SAB là a. Cho SA = a.
	a) Chứng minh rằng và .
	b) Tính thể tích của khối chóp S.ABCD.(ĐS: )
12) Cho tứ diện đều ABCD cạnh a.
	a) Tính độ dài đường cao AH của khối tứ dĩện.(ĐS: )
	b) Gọi M là một điểm bất kỳ trong khối tứ diện. Chứng minh rằng tổng các khoảng cách từ M đến 4 mặt của tứ diện là một số không đổi.
13) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = a và .
	a) Tính diện tích toàn phần của hình chóp.(ĐS: )
	b) Tính thể tích khối nón ngoại tiếp hình chóp S.ABCD.(ĐS: )
	c) Định a để thể tích khối nón là .(ĐS: )
14) Một hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân (AB = AC = a). Đường chéo BC’ của mặt bên BCC’B’ tạo với mặt bên ACC’A’ góc a.
	a) Chứng minh rằng .
	b) Tính diện tích toàn phần của hình lăng trụ. (ĐS: )
	c) Tìm tâm mặt cầu ngoại tiếp hình lăng trụ và tính thể tích khối cầu tương ứng.(ĐS: )
15) Một hình nón có bán kính đáy R và thiết diện qua trục là một tam giác vuông cân.
	a) Tính diện tích xung quanh của hình nón và thể tích khối nón tương ứng.(ĐS: )
	b) Tính bán kính đáy của hình trụ nội tiếp trong hình nón ấy, biết rằng thiết diện qua trục của hình trụ là một hình vuông. (ĐS: )
16) Cho hình cầu tâm O đường kính SS’= 2R. Mặt phẳng vuông góc với SS’ cắt mặt cầu theo đường tròn tâm H. Gọi ABC là tam giác đều nội tiếp trong đường tròn này. Đặt SH = x (R < x < 2R).
	a) Tính độ dài các cạnh của tứ diện S.ABC theo R và x.(ĐS: )
	b) Tính x để cho S.ABC là một tứ diện đều. Trong trường hợp này, tính thể tích của khối tứ diện S.ABC. (ĐS: )
17) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với mặt phẳng đáy.
	a) Tính thể tích của khối chóp S.ABCD.(ĐS: )
	b) Tính góc của cạnh bên SC với mặt phẳng đáy. (ĐS: )
	c) Mặt phẳng (P) qua CD cắt SA tại M; SB tại N. Tứ giác CDMN là hình gì.
18) Trong mp(P) cho tam giác đều ABD nội tiếp đường tròn đường kính AC = 2R. Trên đường vuông góc với mp(P) tại C, lấy điểm M sao cho CM = 2R.
	a) Tính thể tích của khối chóp M.ABCD theo R.(ĐS: )
	b) Gọi I là trung điểm của AM. Chứng minh I.ABD là hình chóp tam giác đều.
	c) Tính thể tích khối chóp I.ABD theo R. (ĐS: )
19) Cho hình nón đỉnh S, bán kính đáy R. Trên đáy của hình nón lấy một lục giác đều ABCDEF. Mp(SAB) hợp với mặt đáy của hình nón góc a.
	a) Tính diện tích thiết diện qua trục của hình nón.(ĐS: )
	b) Tính thể tích của khối chóp S.ABCDEF. (ĐS: )
20) Một hình nón có bán kính đáy R và chiều cao h. Xét hình trụ có chiều cao 2x nội tiếp trong hình nón.
	a) Chứng minh rằng thể tích của khối trụ là .
	b) Định x để V đạt giá  ... SỐ
 Giả sử phải tính 
1/ Đổi biến số dạng 1 :
Phương pháp :
Đặt x = 
Đổi cận tích phân 
Biến đổi f(x) dx = 
Dạng 
 Đặt x = asint với 
Dạng 
Đặt x = atant với 
Ví dụ
Tính các tích phân sau :
1/ 
Đặt x = 2sint với dx= 2costdt
 x = 0 t = 0
 x = 2 t = 
= 
2/ 
Đặt x = 3tant với dx = 3( 1 + tan2t ) dt
x = 0 t = 0
x = 3 
 3/ / K = 
 Ta cã 
§Æt => dx = 
Khi x = 0 => t =; x = 1=> t = 
=>==
 4/ 
Đặt x = 2sint với dx = 2costdt
x = 0 t = 0
x = 1 t = 
 = 
 5/ 
Đặt x = sint với dx = costdt
 I = = 
Bài tập 
Tính các tích phân sau :
1/ Đs : 
2/ Đs : 
3/ 	 Đs : 
4/ Đs : 
2/ Đổi biến số dạng 2 :
Phương pháp :
Đặt u = 
- Đổi cận tích phân 
Ví dụ 
1/ I = 
 Đặt u = u3 = 1 – x 3u2 du = - dx
 x = 0 u = 1
 x = 1 u = 0
 I = = 
2/ I = 
 Đặt u = u3 = 1 – x x = 1-u3 3u2 du = - dx
 x = 0 u = 1
 x = 1 u = 0
 I = = = 
3/ I = 
 Đặt u = x4 + 1 du = 4 x3du x3dx = 
 x = 0 u = 1
 x = 1 u = 2
4/ I = 
 Đặt u = x2 + 1 du = 2xdx xdx = 
 x = 0 u = 1
 x = 1 u = 2
 I = 
 5/ I = 
 Đặt u = 
 xdx = udu
 = 
 6/ I = 
 Đặt u = u3 = x3 – 8 u2du = x2dx
 x = 0 u = -2 
 x = 2 u = 0
7/ I = 
Đặt u = 
Bài tập
1/ I = Đs : 
 2/ I = Đs : 2 
 3 / I = Đs : 
 4/ I = Đs : 
 5/ Đs : ln(e + 1 )
 6 / Đs : 2ln2 - 1
 7/ I = Đs : 
 8/ I = Đs : 
 9/ Đs : 
 11/ I = Đs : 2
 12 / I = Đáp số : 
 13/ I = Đáp số : 
 14/ I = Đáp số : 2e(e- 1) 
 15/ Đáp số : 1
 16/ Đáp số : 
 17/ Đáp số : 
 18/ Đáp số : 
 19/ 
 Đáp số : 
 20/ Đáp số : 
 21/ Đáp số : 
 22/ Đáp số : 
 23/ Đáp số : 
III/ PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN
Phương pháp : giả sử phải tính trong đó P(x) là một đa thức theo x
Nếu Q(x) là sinx hoặc cosx hoặc ex thì đặt u = P(x) ,dv = Q(x)dx
Nếu Q(x) là lnx thì đặt u = Q(x) , dv = P(x)dx
Ví dụ 
1/ 
Đặt u = x du = dx
 dv = 
 2/ 
Đặt u = lnx 
 dv = ( 3x + 2 ) dx v = 
 = 
3/ 
Đặt u = 3 – 2x du = – 2 dx
dv = sinxdx v = - cosx
 = 1
4/ 
 Ñaët u = ln(x – 1) du = 
 dv = 2xdx v = x2 – 1 
 = 48ln2 - 
Bài tập
 Tính các tích phân sau: 
 1/ Đáp số: 
 2/ Đáp số: 
 3/ Đáp số: 
 4/ Đáp số: 
 5/ Đáp số: 
 6/ Đáp số: e - 2
7/ Đáp số: 
8/ Đáp số: 
9/ Đáp số: 
10/ Đáp số: 
ỨNG DỤNG CỦA TÍCH PHÂN
1.Diện tích hình phẳng 
 Cho (C); (C1); (C2) là những đường cong liên tục trên đoạn [a; b] 
1.1.Diện tích hình phẳng (hình thang cong) S giới hạn bởi :
 S = 
Ví dụ
 Tính diện tích hình phẳng giới hạn bởi các đường có phương trình sau :
 1/ , y = 0 , x = 1 , x = e
Giải
 Ta có f(x) > 0 [1;e] 
 Đặt u = u2 = 1 + lnx 2udu = 
 x = 1 u = 1
 x = e u = 
 S = = (đvdt)
2/ , y = 0 , x = 0 , x = 1
Giải
 = 
Đặt u = u2 = 1 + x2 x2 = u2 - 1 xdx = udu
 x = 0 u = 1
 x = 1 u = 
 S = (đvdt)
Bài tập
 Tính diện tích hình phẳng giới hạn bởi các đường có phương trình sau :
1/ y = x2 - 4x + 3 , y = 0 , x = 2 , x = 4. Đáp số: 2
2/ y = - x2 + 3x , y = 0 , x = -1 , x = 1 Đáp số: 3
3/ y = sin2x.cos3x , y = 0 , , , Đáp số: (đvdt)
4/ y = , y = 0 , x = 0 , x = Đáp số : (đvdt)
5/ y = xln2x , y = 0 , x = 1 , x = e Đáp số : (đvdt)
6/ y = sin4x + cos4x , y = 0 , x = và x = Đáp số : (đvdt)
1.2.Diện tích hình phẳng S giới hạn bởi:
 S = 
Phương pháp 
- Giải phương trình f(x) - g(x) = 0 ( 1 )
- Nếu pt (1) có 1 nghiệm csao cho thì :
 S = 
-Nếu pt (1) có 2 nghiệm sao cho thì :
 S = 
Ví dụ
 Tính diện tích hình phẳng giới hạn bởi các đường có phương trình sau :
1/ y = x2 - 4 , y = - x2 - 2x , x = - 2 , x = 2
Giải
 Giải pt (x2 - 4) - ( - x2 - 2x) = 0
2x2 + 2x - 4 = 0
 = (đvdt)
1.3.Diện tích hình phẳng S giới hạn bởi:
Phương pháp 
- Giải phương trình f(x) - g(x) = 0 ( 1 )
- Nếu pt (1) có 2 nghiệm a, b (a < b ) thì :
 S = 
-Nếu pt (1) có 3 nghiệm a , b , c sao cho a < b< c thì :
 S = 
Ví dụ : Tính diện tích hình phẳng giới hạn bởi các đường có phương trình sau :
 , .
Giải
 Giải pt ( x2 - 2x) - (- x2 + 4x ) = 0
2x2 - 6x = 0
 S = = 9 (đvdt)
Bài tập
 Tính diện tích hình phẳng giới hạn bởi các đường có phương trình sau :
1/ , y = x , x = 0 , x = 2 Đáp số: 
2/ y = 2 - x2 , y = x , x = 0 , x = 1 Đáp số: 
3/ y = 2 - x2 , y = x Đáp số: 
4/ y = , y = 6 - x và trục hoành Đáp số: 
5/ y = 7 - 2x2  , y = x2 + 4 Đáp số: 4 
6/ x - y2 = 0 và x + 2y2 = 3 Đáp số: 4
7/ x = y3 - y2 và x = 2y Đáp số: 
2.Thể tích của vật thể 
& Khi cho hình thang cong giới hạn bởi 
quay quanh trục Ox ta
được vật thể tròn xoay (T) 
có thể tích: V = 
Ví dụ
 Tính thể tích vật thể tròn xoay sinh ra khi cho hình phẳng ( H ) giới hạn bởi các đường sau quay quanh trục Ox : y = , y = 0 , x = 0 , x = 3
Giải
 = (đvtt)
Bài tập
	 Tính thể tích vật thể tròn xoay sinh ra khi cho hình phẳng ( H ) giới hạn bởi các đường sau quay quanh trục Ox : 
1/ y = x2 - 4x + 4 , y = 0 , x = 0 , x = 3 Đáp số: V = ( đvtt )
2/ y = 2 - x2 , y = 1 Đáp số: ( đvtt ) 
3/ y = 2x - x2 , y = x Đáp số: (đvtt )
4/ và đường thẳng x = 2: 	Đáp số: (đvtt) 
5/ và trục hoành: 	Đáp số: (đvtt)
6/ 	 Đáp số: (đvtt)
& Khi cho hình thang cong giới hạn bởi
quay quanh trục Oy ta
được vật thể tròn xoay (T) có thể tích : V = 
Ví dụ
 Tính thể tích vật thể tròn xoay sinh ra khi cho hình phẳng ( H ) giới hạn bởi các đường sau quay quanh trục Oy : , x = 0 ,y = -1 , y = 1
Giải
 = 
Bài tập
 Tính thể tích vật thể tròn xoay sinh ra khi cho hình phẳng ( H ) giới hạn bởi các đường sau quay quanh trục Oy :
1/ x ( y + 1 ) , x = 0 , y = 0 , y = 3 Đáp số: : ( đvtt )
2/ y = lnx , y = 0 , x = e Đáp số: : ( đvtt)
3/ và đường thẳng x = 2: 	 Đáp số: (đvtt)
4/ và trục hoành: 	 Đáp số: (đvtt)
5/ quay quanh trục Oy.	 Đáp số: (đvtt)
--------------------------------
 SỐ PHỨC
TÓM TẮT LÝ THUYẾT
I. DẠNG ĐẠI SỐ CỦA SỐ PHỨC: 
* Một số phức là một biểu thức dạng a + bi, trong đó a, b là số thực và số i thỏa mãn i2 = -1. Kí hiệu số phức là z và viết z = a + bi
* Tập hợp các số phức được kí hiệu bằng C.
* i được gọi là đơn vị ảo, a được gọi là phần thực và b được gọi là phần ảo của số phức z = a + bi.
* Số thực a được coi là một số phức có phần ảo bằng 0 : z = a + 0i = a . Số phức có phần thực bằng 0 được gọi là số ảo : z = 0 + bi, b .
* Ta có i = 0 + 1i = 1i
* Số 0 là số phức duy nhất vừa là số thực, vừa là số ảo.
II. BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC
	Mỗi số phức z = a + bi được biểu diễn bỡi một điểm M(a, b) trên mặt phẳng tọa độ Oxy. Mặt phẳng tọa độ với việc biểu diễn số phức như thế được gọi là mặt phẳng phức. Trục Ox được gọi là trục thực, trục Oy được gọi là trục ảo.
 y M(z)
 b 
 a
III. CÁC PHÉP TOÁN TRÊN SỐ PHỨC : 
Cho hai số phức z = a + bi (a, b ); z’ = a’ + b’i (a’, b’ ).
	i. 	z = z’ a = a’ và b = b’
	ii. 	z + z’ = (a + a’) + (b + b’)i
	iii.	z – z’ = (a – a’) + (b – b’)i
	iv. 	z.z’ = (aa’ – bb’) + (ab’ + a’b)i 
	v. 	Số đối của z là – z = – a – bi
	vi. 	Số phức liên hợp của z là 
	vii. 	Môđun của z là 
viii.	 Số nghịch đảo của z là = 
	ix. 	 ; 
x. 	Với z 0 thì 
IV. CĂN BẬC HAI CỦA SỐ PHỨC
Cho số phức w. Mỗi số phức z thỏa mãn z2 = w được gọi là một căn bậc hai của w.
Tính chất: Cho số phức w, căn bậc hai của w có các tính chất:
	i. 	w = 0 có đúng một căn bậc hai là z = 0.
	ii.	w 0 có đúng hai căn bậc hai đối nhau khác không thỏa z2 = w
	iii. 	Số thực a > 0 có hai căn bậc hai là 
	Số thực a < 0 có hai căn bậc hai là 
Chú ý : Cách tìm căn bậc hai của một số phức 
	Cho số phức w = a + bi và z = x = iy là căn bậc hai của số phức w. Ta có (x ; y) là nghiệm của hệ phương trình :	
V. PHƯƠNG TRÌNH BẬC HAI  
Cho phương trình bậc hai az2 + bz + c = 0 ; a 0 , a,b,c là các số phức.
i.	Gọi z1, z2 là nghiệm của phương trình thì . Trong đó là một căn bậc hai của 
ii.	Khi = 0 thì 
iii.	Khi là số thực dương thì 	 
iv.	Khi là số thực âm thì 	 
VI. DẠNG LƯỢNG GIÁC CỦA SỐ PHỨC
1. Acgumen của số phức
	i. Định nghĩa : Cho số phức z 0. Gọi M là một điểm trên mặt phẳng phức biểu diễn số z. Số đo ( radian ) của mỗi góc lượng giác (Ox, OM) được gọi là một acgumen của z
 y
 b M(z)
 O a x
ii. Nếu là một acgumen của z thì mọi acgumen của z có dạng , k 
iii. Hai số phức z và lz ( z 0 và l là một số dương ) có cùng acgumen.
2. Dạng lượng giác của số phức
	i. Kí hiệu thì và là một acgumen của z thì số phức z = a + bi 0 có thể viết dưới dạng z = r(cos + i.sin). Được gọi là dạng lương giác của số phức z
	ii. Để tìm dạng lượng giác của một số phức z = a + bi 0 ta tìm:
	+ 
	+ góc sao cho 
	iii. Chú ý:
+ Ta xem 
+ Điều kiện r > 0 trong dạng lượng giác r(cos + i.sin) của số phức z 0 .
3. Nhân, chia số phức dưới dạng lượng giác
	Nếu z = r(cos + i.sin) và z’ = r’(cos’ + i.sin’); r, r’ 0
 Thì 
	Và 
4. Công thức Moivre
	i. Công thức Moivre: 
 	 Khi r = 1, ta có: 
	ii. Căn bậc hai của số phức dạng lượng giác
	Cho z = r(cos + i.sin), r 0 thì z có hai căn bậc hai là 
	 và – = 
BÀI TẬP THỰC HÀNH
1. Thực hiện Các phép tính 
	a. 	b. 
Đáp số :	a. 0	b. 
2. Giải các phương trình :
a. (3 + 4i)z = (1 + 2i)(4 + i)	b. 2iz + 3 = 5z + 4i	 c. 3z(2 – i) + 1 = 2iz(1 + i) + 3i
Đáp số: 	a. 	b. 	 c. 
3. Tính : 1 + (1 + i) + (1 + i)2 + (1 + i)3 +  + (1 + i)20
Hướng dẫn: Tính tổng cấp số nhân có công bội là 1 + i
Đáp số: 	-210 + (210 + 1)i.
4. Tìm x và y để:
	a. (x + 2y)2 = yi	b. (x – 2i)2 = 3x + yi
Đáp số: 	a. 	b. 
5. Tính:
	a. (1 + i)2	b. (1 + i)3	c. (1 + i)4	d. (1 + i)5
Đáp số: 	a. 2i	b. -2 + 2i	c. -4	d. -4 – 4i 
6. Tính căn bậc hai của số phức sau:
a. 	b. 16 – 30i	c. 8 + 6i	d. 1 – i
Đáp số:a. 	b. 	c. 	d. 
7. Giải các phương trình:
a. 2z2 + 3z + 5	= 0	b. z2 – (2+ i)z	+ (-1 + 7i) = 0
c. z2 + (3 – 2i )z + (5 – 5i) = 0	d. z4 – 3z2 + 4 = 0
Đáp số:	a. 	b. 3 – i, -1 + 2i
	c. -1 + 3i, -1 – i	d. 
8. Gọi là hai nghiệm của phương trình: z2 + (2 – i)z + 3 + 5i = 0. Không giải phương trình, hãy tính:
a. 	b. 	c. 	d. 
Đáp số:	a. -3 - 14i	b. -55 + 24i	c. 	d. -63 + 99i
9. Giải các phương trình :
	a. z3 – 1 = 0	b. z3 + 1 = 0	c. z4 – 1 = 0	d. z4 + 1 = 0
Đáp số: 	a. 	b. -
	c. 1; i; -1; -i	d. 
10. Tìm phần thực và phần ảo của số phức sau:
	a. 	b. 
	c. 	d. 
Đáp số: a. 1 và 1	b. 	c. 	d. 
11. Viết các số phức sau dưới dạng lượng giác
	a. 	b. 	c. 	d. 3
Đáp số: a. 	b. 
	 c. 	d. 
12. Thực hiện các phép tính: Cho z1 = và z2 = . Tính:
	a. z1.z2	b. 	c. 
Đáp số: a. 	b. 	c. 
13. Dùng công thức Moivrơ chứng minh các công thức:
a. cos3 = 4cos3 – 3 cos	b. sin3 = 3sin – 4sin3.
Hướng dẫn: 	 
Từ công thức Moivre ta có: 
Mặt khác:
14. Cho số phức z = . Tìm số phức w sao cho w3 = z.
Hướng dẫn:	Đặt 
Ta có 
Đáp số: 	
15. Tìm căn bậc hai của các số phức:
	a. 	b. 
Đáp số: 	a. ; 
	b. ; 	
15. Giải phương trình 
Hướng dẫn: 	Đặt z = a + bi
Đáp số:	
16. Giải hệ phương trình: 
Hướng dẫn:	Đặt z = a + bi
Đáp số:	z = 1 + i
Giáo viên biên soạn
1. Trần Toàn ( THPT Tây Ninh)
Hình học không gian tổng hợp.
2.Lê Thị Thuý Oanh (THPT Dương Minh Châu)
Toạ độ trong không gian + Mặt cầu.
3. Lương văn Mẫn ( THPT Nguyễn Trãi)
Đường thẳng và mặt phẳng trong không gian.
4. Dương Thanh Hồng ( THPT Lý Thường Kiệt)
Khảo sát hàm số đa thức.
5. Mai Hữu Trí ( THPT Nguyễn Chí Thanh)
Khảo sát hàm số phân thức.
6. Huỳnh Ngọc Chân ( THPT Nguyễn Văn Trỗi)
Phương trình Mũ – Logarit.
7. Đỗ Gia Phước (THPT Nguyễn Huệ)
Nguyên hàm và Tích phân.
8. Bùi Trọng Thế (THPT Chuyên Hoàng Lê Kha)
Số phức