Tài liệu luyện thi đại học - Phương trình và bất phương trình chứa căn thức
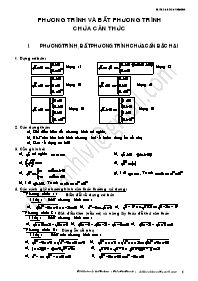
2. Các dạng khác:
a). Đặt điều kiện để phương trình có nghĩa.
b). Khử căn bậc hai: bình phương hai vế hoặc dùng ẩn số phụ
c). Đưa về dạng cơ bản
Bạn đang xem tài liệu "Tài liệu luyện thi đại học - Phương trình và bất phương trình chứa căn thức", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH CHỨA CĂN THỨC PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH CHỨA CĂN BẬC HAI 1. Dạng cơ bản: (dạng 1) (dạng 2) (dạng 3) (dạng 4) (dạng 5) (dạng 6) 2. Các dạng khác: a). Đặt điều kiện để phương trình có nghĩa. b). Khử căn bậc hai: bình phương hai vế hoặc dùng ẩn số phụ c). Đưa về dạng cơ bản 3. Cần ghi nhớ: a). có nghĩa b). c). d). e). g). Với . Ta có: h). Với . Ta có: 4. Các cách giải phương trình căn thức thường sử dụng : * Phương pháp 1 : Biến đổi về dạng cơ bản Ví dụ : Giải phương trình sau : a). b). c). * Phương pháp 2 : Đặt điều kiện (nếu có) và nâng lũy thừa để khử căn thức Ví dụ : Giải phương trình sau : a). b). c). * Phương pháp 3 : Dùng ẩn số phụ Ví dụ : Giải các phương trình sau : a). b). c). d). e). f). *Phương pháp 4 : Biến đổi phương trình về dạng tích số Ví dụ : Giải phương trình sau : * Phương pháp 5 : Nhẩm nghiệm và sử dụng tính đơn điệu để chứng minh nghiệm duy nhất * Ta thường sử dụng các tính chất sau: Tính chất 1: Nếu hàm số f tăng ( hoặc giảm ) trong khoảng (a;b) thì phương trình f(x) = C có không quá một nghiệm trong khoảng (a;b). Tính chất 2 : Nếu hàm f tăng trong khoảng (a;b) và hàm g là hàm hằng hoặc là một hàm giảm trong khoảng (a;b) thì phương trình f(x) = g(x) có nhiều nhất một nghiệm trong khoảng (a;b) . Do đó: Nếu tồn tại x0 (a;b) sao cho f(x0) = g(x0) thì đó là nghiệm duy nhất của phương trình f(x) = g(x)) Ví dụ : Giải các phương trình sau : 1. 2. Bài tập tương tự: 1) (x=3) 2) (x=4) 5. Các cách giải bất phương trình căn thức thường sử dụng : * Phương pháp 1 : Biến đổi về dạng cơ bản Ví dụ : Giải các bất phương trình sau : a) b) * Phương pháp 2 : Đặt điều kiện (nếu có) và nâng lũy thừa để khử căn thức Ví dụ : Giải bất phương trình sau : a). b). (K.B98) c). (K.A98) d). (KA2004) * Phương pháp 3 : Dùng ẩn số phụ Ví dụ : Giải phương trình sau : a). b). c). d). (GTVT98) * Phương pháp 4 : Biến đổi phương trình về dạng tích số hoặc thương số Ví dụ : Giải các bất phương trình sau : a) (K.D2002) b) c). (NNHN98) d). (KA99) 6. Bài tập làm thêm: B1. Giải phương trình: a). b). c). d). e). f). B2. Giải phương trình: a). b). c). d) e) f). B3. Giải phương trình: a). b). c). d). B4. Giải phương trình: a). b). B5. Giải phương trình: ( HD đặt ) B6. Giải bất phương trình: a). b). c). d). B7. Giải bất phương trình: a). b). c). d). B8. Giải bất phương trình a). b). c). B9. Giải bất phương trình a). b). c). d). e). f). B10. Giải bất phương trình a). b). II. GIẢI PHƯƠNG TRÌNH CHỨA CĂN BẬC 3 1. Dạng cơ bản: (dạng 1) (dạng 2) 2. Dạng khác: (1) a). Tam thừa 2 vế của (1) b). Thay bởi , ta được: (2) c). Giải (2) và thử lại các nghiệm 3. Các ví dụ: a). b). (SP96) c). 4. Bài tập làm thêm: B1. Giải phương trình: a). b). B2. Giải phương trình: (GTVT99) B3. Giải phương trình ( HD đặt ) III. GIẢI VÀ BIỆN LUẬN PHƯƠNG TRÌNH CHỨA CĂN THỨC 1. Cần ghi nhớ: 1). Với bài toán "Giải và biện luận phương trình chứa căn thức". Cần giải quyết 3 vấn đề: a/. Điều kiện có nghiệm ? b/. Có bao nhiêu nghiệm ? c/. nghiệm số bằng bao nhiêu ? 2). Với bài toán "Biện luận số nghiệm của phương trình". Cần giải quyết 2 vấn đề: a/. Điều kiện có nghiệm ? b/. Có bao nhiêu nghiệm ? 3). Với bài toán "Tìm m để phương trình f(x) = m có nghiệm". Có thể dùng phương pháp đồ thị để giải quyết và ta có tính chất sau: phương trình f(x) = m có nghiệm 2. Các ví dụ: VD1: Giải và biện luận phương trình: a). b). VD2: Tìm điều kiện của tham số m để phương trình sau có nghiệm a). b). VD3: Biện luận theo m số nghiệm của phương trình a). b). 3. Bài tập làm thêm: B1. Biện luận theo m số nghiệm của phương trình a). b). B2. Tìm m để phương trình có nghiệm a). b). c). d). d). e). B3. Giải và biện luận phương trình: (QGHN99) IV. GIẢI VÀ BIỆN LUẬN BẤT PHƯƠNG TRÌNH CHỨA CĂN THỨC 1. Cần ghi nhớ: 1.1) Với bài toán "Giải và biện luận bất phương trình chứa căn thức".T a cần thực hiện theo các bước như sau: b1). Đặt điều kiện để các biểu thức chứa căn có nghĩa b2). Biến đổi tương đương để tìm x b3). Kiểm tra các điều kiện và kết luận 1.2) Với bài toán "Tìm m để bất phương trình có nghiệm " hoặc "Tìm m để bất phương trình nghiệm đúng với mọi ". Ta dùng phương pháp max, min Tính chất 1: bất phương trình có nghiệm bất phương trình có nghiệm Tính chất 2: bất phương trình nghiệm đúng với mọi bất phương trình nghiệm đúng với mọi 2. Các ví dụ: VD1: Giải và biện luận bất phương trình a). b). VD2: Cho bất phương trình: (1) 1). Giải bất phương trình khi m = 3 2). Tìm để bất phương trình (1) nghiệm đúng với mọi VD3: Tìm m để hàm số không nhận giá trị dương với mọi VD4: Cho bất phương trình: (1) 1). Giải bất phương trình khi 2). Tìm m để bất phương trình (1) có nghiệm 3. Bài tập làm thêm: B1. Giải và biện luận bất phương trình: 1. 2. (a>0) B2. Tìm m để bất phương trình: a). nghiệm đúng với mọi b). nghiệm đúng với mọi V. HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC 1. Cần ghi nhớ: a). Đặt điều kiện để các biểu thức chứa căn có nghĩa b). Dùng các phép: Thế hoặc khử hoặc dùng ẩn phụ đưa về hệ đã biết cách giải c). Kiểm tra các điều kiện và kết luận 2. Bài tập làm thêm: B1. Cho hệ phương trình 1). Giải hệ phương trình khi a = 4 2). Tìm a để hệ phương trình có nghiệm B2. Giải hệ phương trình a). b). B3. Giải hệ phương trình a). b). B4. Giải hệ phương trình a). b).
Tài liệu đính kèm:
 PTvaBPT canthuc 2009 cuchot.doc
PTvaBPT canthuc 2009 cuchot.doc





