Ôn thi tốt nghiệp Toán lớp 12
KHẢO SÁT HÀM SỐ VÀ CÂU HỎI PHỤ
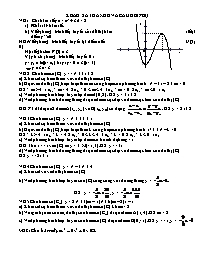
VD1 : Cho hàm số y = - x3 + 3x2 - 2
a) Khảo sát hàm số.
b) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm y’’=0
HD: Viết phương trình tiếp tuyến tại điểm uốn U(1 ; 0)
Hệ số góc k = f’(1) = 3
Vậy ta có phương trình tiếp tuyến là :
y - y0 = k(x - x0) hay : y - 0 = 3(x - 1)
y = 3x - 3
Bạn đang xem 20 trang mẫu của tài liệu "Ôn thi tốt nghiệp Toán lớp 12", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
KHẢO SÁT HÀM SỐ VÀ CÂU HỎI PHỤ
2
-
2
y
x
O
VD1 : Cho hàm số y = - x3 + 3x2 - 2
Khảo sát hàm số.
Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm y’’=0
HD: Viết phương trình tiếp tuyến tại điểm uốn U(1 ; 0)
Hệ số góc k = f’(1) = 3
Vậy ta có phương trình tiếp tuyến là :
y - y0 = k(x - x0) hay : y - 0 = 3(x - 1)
Û y = 3x - 3
VD 2: Cho hàm số (C): y = -x3 + 3x + 2
a) Khảo sỏt sự biến thiờn và vẽ đồ thị hàm số (C)
b) Dựa vào đồ thị (C), biện luận theo m số nghiệm của phương trỡnh: x3 – 3x – 2 + m = 0
ĐS: * m > 4: 1 n0; * m = 4: 2 n0; * 0 < m < 4: 3 n0; * m = 0: 2 n0; * m < 0: 1 n0
c) Viết phương trỡnh tiếp tuyến tại điểm I(0; 2). ĐS: y = 3x + 2
d) Viết phương trỡnh đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị (C)
HD: PT đt đi qua 2 điểm A(xA; yA) và B(xB; yB) cú dạng: . ĐS: y = 2x + 2
VD3: Cho hàm số (C): y = x3 + 3x2 + 1
a) Khảo sỏt sự biến thiờn và vẽ đồ thị hàm số (C)
b) Dựa vào đồ thị (C), biện luận theo k số nghiệm của phương trỡnh: x3 + 3x2 – k = 0
ĐS: * k > 4: 1 n0; * k = 4: 2 n0; * 0 < k < 4: 3 n0; * k = 0: 2 n0; * k < 0: 1 n0
c) Viết phương trỡnh tiếp tuyến tại điểm cú hoành độ bằng -1
HD: Thế x = -1 vào (C) y = 3: M(-1; 3). ĐS: y = -3x
d) Viết phương trỡnh đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị (C)
ĐS: y = -2x + 1
VD4: Cho hàm số (C): y = x3 – 3x2 + 4
a) Khảo sỏt và vẽ đồ thị hàm số (C)
b) Viết phương trỡnh tiếp tuyến của (C) song song với đường thẳng y = .
ĐS: y = ; y =
VD5: Cho hàm số (Cm): y = 2x3 + 3(m – 1)x2 + 6(m – 2)x – 1
a) Khảo sỏt sự biến thiờn và vẽ đồ thị hàm số (C) khi m = 2
b) Với giỏ trị nào của m, đồ thị của hàm số (Cm) đi qua điểm A(1; 4). ĐS: m = 2
c) Viết phương trỡnh tiếp tuyến của hàm số (C) đi qua điểm B(0; -1). ĐS: y = -1; y =
VD5: Cho haứm soỏ y=x3 – 6x2 + 9x (C).
Duứng ủoà thũ (C) bieọn luaọn soỏ nghieọm cuỷa phửụng trỡnh x3 – 6x2 + 9x – m = 0
Giaỷi:
Phửụng trỡnh x3 – 6x2 + 9x – m = 0
x3 – 6x2 + 9x = m
Soỏ nghieọm cuỷa phửụng trỡnh laứ soỏ giao
ủieồm cuỷa ủoà thũ (C) vaứ ủửụứng thaỳng d: y=m.
dửùa vaứo ủoà thũ ta coự:
Neỏu m > 4 phửụng trỡnh coự 1 nghieọm.
Neỏu m = 4 phửụng trỡnh coự 2 nghieọm.
Neỏu 0< m <4 phửụng trỡnh coự 3 nghieọm.
Neỏu m=0 phửụng trỡnh coự 2 nghieọm.
Neỏu m < 0 phửụng trỡnh coự 1 nghieọm.
VD7: Cho hàm số
Khảo sát hàm số
Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng 1.
Giải:
Khảo sát hàm số
Tập xác định: R
Sự biến thiên
Giới hạn:
Bảng biến thiên:
x
-∞ - 2 0 2 +∞
y’
+ 0 - 0 + 0 -
y
-∞ -∞
Suy ra hàm số đồng biến trên khoảng (-∞; -2) và (0; 2), nghịch biến trên khoảng ( -2; 0) và (2; +∞)
6
4
2
y
5
x
O
1
Cực trị:
Đồ thị : (H2)
Điểm uốn: y” = - 3x2 +4; y” = 0
Giao với Ox : A(-3 ; 0) và B(3 ; 0)
Giao Oy :
(H2)
x0 = 1 ị y0 = 4, y’(x0) = y’(1) = 3. Nên phương trình tiếp tuyến cần tìm là : y - 4 = 3(x - 1), hay : y = 3x + 1.
VD8: Cho hàm số (C): y = - x4 + 2x2 + 1
a) Khảo sỏt sự biến thiờn và vẽ đồ thị hàm số (C)
b) Biện luận theo m số nghiệm của phương trỡnh: -x4 + 2x2 + 1 – m = 0
ĐS: * m > 2: vụ n0; * m = 2: 2 n0; * 1 < m < 2: 4 n0; * m = 1: 3 n0; * m < 1: 2 n0
c) Viết phương trỡnh tiếp tuyến tại điểm cú tung độ bằng 2
HD: Thế y = 2 vào (C) x =1: M(-1; 2), N(1; 2). ĐS: y = 2
VD9: Cho hàm số (C): y = x4 – 2x2 – 3
a) Khảo sỏt và vẽ đồ thị hàm số (C)
b) Viết phương trỡnh tiếp tuyến của (C), biết hệ số gúc của tiếp tuyến là 24. ĐS: y = 24 – 43
VD10: Cho hàm số (Cm): y = x4 – (m + 7)x2 + 2m – 1
a) Khảo sỏt sự biến thiờn và vẽ đồ thị hàm số (C) khi m = 1
b) Xỏc định m để đồ thị (Cm) đi qua điểm A(-1; 10). ĐS: m = 1
c) Dựa vào đồ thị (C), với giỏ trị nào của k thỡ phương trỡnh: x4 – 8x2 – k = 0 cú 4 nghiệm phõn biệt. ĐS: -14 < k < 0
VD11: Cho hàm số:
Khảo sát hàm số.
Xác định toạ độ giao điểm của (C) với đường thẳng d: y = 2x + 2. Viết phương trình tiếp tuyến của (C) tại các giao điểm trên.
Giải:
Khảo sát hàm số:
1.Tập xác định: D = R\{1}
2.Sự biến thiên:
Chiều biến thiên:
.
Nên hàm số nghịch biến trên (-∞; 1) và (1; +∞)
Cực trị: Đồ thị hàm số không có cực trị.
Giới hạn và tiệm cận:
ị x = 1 là tiệm cận đứng.
ị y = - 1 là tiệm cận ngang.
2
-
2
-
4
y
5
x
1
O
I
Bảng biến thiên :
x
-∞ 1 +∞
y’
- -
y
+∞
-1 -1
-∞
3.Đồ thị : (H3)
- Giao với Ox : A(4 ; 0)
- Giao với Oy : B(0 ; -4)
- Đồ thị nhận I(1 ; - 1)
làm tâm đối xứng
Hoành độ giao điểm của(C)
và đường thẳng d là nghiệm
Của phương trình:
Vậy giao điểm của (C) và đường thẳng d là:
- Phương trình tiếp tuyến của (C) tại M1 có hệ số góc là:
Nên có phương trình là:
- Phương trình tiếp của (C) tại M2 có hệ số góc là: . Nên có phương trình là:
VD12. Cho hàm số có đồ thị (C).
1) Khảo sát hàm số.
2) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x = -1
3) Tìm GTLN và GTNN của hàm số trên [0; 2].
Hướng dẫn giải.
1) Hs tự khảo sát. Đồ thị:
2) Có ;
ị Phương trình tiếp tuyến:
3) Ta có hàm số nghịch biến trên các khoảng xác định nên hàm số nghịch biến trên [0; 2].
Do đó: .
VD13. Cho hàm số (C): y =
a) Khảo sỏt và vẽ đồ thị hàm số (C)
b) Viết phương trỡnh tiếp tuyến của (C) vuụng gúc với đường phõn giỏc phần tư thứ nhất
HD: Đường phõn giỏc phần tư thứ nhất là: y = x. ĐS: y = -x và y = -x + 8
VD14.: Cho hàm số (Cm): y =
a) Khảo sỏt sự biến thiờn và vẽ đồ thị hàm số (C2)
b) Chứng minh rằng với mọi giỏ trị của tham số m, hàm số luụn đồng biến trờn mỗi khoảng xỏc định của nú
HD: Chứng minh tử thức của y’ > 0 suy ra y’ > 0(đpcm)
c) Xỏc định m để tiệm cận đứng của đồ thị đi qua A(-1; ). ĐS: m = 2
d) Viết phương trỡnh tiếp tuyến của hàm số (C2) tại điểm (1; ). ĐS: y =
VD15: Cho hàm số (Cm): y =
a) Khảo sỏt sự biến thiờn và vẽ đồ thị hàm số (C) khi m = 0
b) Với giỏ trị nào của m, đồ thị của hàm số (Cm) đi qua điểm B(0; -1). ĐS: m = 0
c) Định m để tiệm cận ngang của đồ thị đi qua điểm C(; -3). ĐS: m = -4
c) Viết phương trỡnh tiếp tuyến của hàm số tại giao điểm của nú với trục tung
HD: Giao điểm với trục tung x = 0, thay x = 0 vào (C) y = -1: E(0; -1). ĐS: y = -2x – 1
TèM GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ trờn D
A. Hai cỏch thường dựng.
Cỏch 1: - Lập bảng biến thiờn của hàm số trờn D.
- Từ bảng biến thiờn suy ra GTLN, GTNN .
Cỏch 2: Nếu liờn tục trờn D = [a;b]
- Tỡm cỏc điểmtrờn khoảng (a;b) mà tại đú bằng 0 hoặc khụng tồn tại.
- Tớnh .
- Tỡm số lớn nhất M và số nhỏ nhất m trong cỏc số trờn.
- Ta cú .
B. Bài tập.
Tỡm GTLN, GTNN của hàm số trờn đoạn [-3;5].
(ĐS: )
Tỡm GTLN, GTNN của hàm số trờn đoạn [3;5].
(ĐS: )
Tỡm GTLN, GTNN của hàm số trờn khoảng .
(ĐS: , khụng cú GTNN )
Tỡm GTLN, GTNN của hàm số .
(ĐS: )
Tỡm GTLN, GTNN của hàm số trờn đoạn [-2;2].
(ĐS: )
Tỡm GTLN, GTNN của hàm số .
(ĐS: ,)
Tỡm GTLN, GTNN của hàm số trờn đoạn .
(ĐS: ,)
Tỡm GTLN, GTNN của hàm số .
(ĐS: ,)
Tỡm GTLN, GTNN của hàm số trờn đoạn .
(ĐS: )
Tỡm GTLN, GTNN của hàm số trờn đoạn [-2;2].
(ĐS: )
BÀI TẬP LÀM THấM
y = x4 – 2x2 + 1 trờn đọan [-1;2].
y = .
y = trờn đọan [ 1; e ].
y = sin2x – x trờn đọan .
y = x – lnx + 3.
với
trờn đoạn [ -1;3].
y = trờn
y = trờn
trờn đoạn
trờn đoạn [-2 ;0]
y = (x – 6) trờn đoạn [0 ; 3].
y = x+
y = 2sin2x + 2sinx – 1
trờn đoạn [-1;1].
trờn đoạn [-3;3].
trờn đoạn [-1;1].
trờn đoạn [-2;-1].
trờn đoạn [-4;0].
trờn khoảng ( 0 ; +∞ ).
trờn đoạn [1;3].
trờn đoạn
trờn khoảng (1 ; +∞ ).
trờn đoạn [0;2].
trờn đoạn [-4;4].
trờn đoạn
trờn đoạn [0;3].
trờn đoạn [-2;2].
trờn đoạn [0;1].
(x > 5 )
trờn đoạn
trờn đoạn [-1;0].
trờn đoạn
trờn khoảng .
trờn đoạn
trờn đoạn
Chuyên Đề 2: Hàm Số Mũ và Lôgarit
1. Phương phỏp: Biến đổi phương trỡnh về dạng cựng cơ số: aM = aN M = N
Vớ dụ 1: Giải cỏc phương trỡnh sau :
HD:
Vậy phương trỡnh cú nghiệm:
Vớ dụ 2: Giải cỏc phương trỡnh sau :
HD:
Vậy phương trỡnh cú nghiệm:
Vớ dụ 3: Giải phương trỡnh sau :
HD:
Vậy phương trỡnh cú nghiệm:
Vớ dụ 4: Giải phương trỡnh sau :
HD:
Vậy phương trỡnh cú nghiệm:
2. Phương phỏp: Đặt ẩn phụ chuyển về phương trỡnh đại số
Vớ dụ 1: Giải cỏc phương trỡnh sau :
HD:
(*)
Đặt
Phương trỡnh (*)
Với
Với
Vậy phương trỡnh cú nghiệm:
Vớ dụ 2: Giải cỏc phương trỡnh sau :
HD: (*)
Đặt
Phương trỡnh (*)
Với
Vậy phương trỡnh cú nghiệm:
Vớ dụ 3: Giải cỏc phương trỡnh sau :
HD: (*)
Đặt
Pt (*)
Với
Vậy phương trỡnh cú nghiệm:
3. Phương phỏp: Lấy logarit hai vế
Vớ dụ 1: Giải phương trỡnh sau :
HD: Lấy logarit hai vế với cơ số 8, ta được
Vậy phương trỡnh cú nghiệm:
Vớ dụ 2: Giải phương trỡnh sau :
HD: Lấy logarit hai vế với cơ số 3, ta được
Vậy phương trỡnh cú nghiệm:
II. BẤT PHƯƠNG TRèNH MŨ
1. Phương trỡnh cơ bản:
a.
Phương trỡnh vụ số nghiệm
Phương trỡnh :
b.
Phương trỡnh vụ nghiệm
Phương trỡnh :
Vớ dụ 1: Giải bất phương trỡnh:
Vậy bất phương trỡnh cú nghiệm:
Vớ dụ 2: Giải bất phương trỡnh:
Vậy bất phương trỡnh cú nghiệm:
2. Phương phỏp: Biến đổi bất phương trỡnh về dạng cựng cơ số:
a.
b.
Vớ dụ 1: Giải bất phương trỡnh:
HD:
Vậy bất phương trỡnh cú nghiệm:
Vớ dụ 2: Giải bất phương trỡnh: (1)
HD: Ta cú:
Phương trỡnh (1)
Vậy bất phương trỡnh cú nghiệm:
3. Phương phỏp: Đặt ẩn phụ chuyển về bất phương trỡnh đại số.
Vớ dụ 1: Giải bất phương trỡnh:
HD: (1)
Đặt
Ta cú: (1)
Vậy bất phương trỡnh cú nghiệm:
Vớ dụ 2: Giải bất phương trỡnh:
HD: (1)
Đặt .
Ta cú: (1)
Vậy bất phương trỡnh cú nghiệm:
Vớ dụ 3: Giải bất phương trỡnh:
HD: Chia (*) hai vế cho ta được: (**)
Đặt .
Ta cú: (**)
Vậy bất phương trỡnh cú nghiệm:
PHƯƠNG TRèNH LễGARIT
1. Phương phỏp : Biến đổi phương trỡnh về dạng cựng cơ số:
Vớ dụ 1 : Giải phương trỡnh sau :
HD: (1)
Điều kiện:
Do đú phương trỡnh
Vậy phương trỡnh cú nghiệm:
Vớ dụ 2 : Giải phương trỡnh sau :
HD: (1)
Điều kiện:
Phương trỡnh
Vậy phương trỡnh cú nghiệm
2. Phương phỏp : Đặt ẩn phụ chuyển về phương trỡnh đại số.
Vớ dụ 1: Giải cỏc phương trỡnh sau :
HD: (1)
Điều kiện:
Phương trỡnh
Đặt
Lỳc đú:
Vậy phương trỡnh cú nghiệm
Vớ dụ 2: Giải cỏc phương trỡnh sau :
HD: (1)
Điều kiện:
Phương trỡnh
(2)
Đặt
Lỳc đú: phương trỡnh (2)
thỏa (*)
Vậy phương trỡnh cú nghiệm
3. Phương phỏp: Mũ húa hai vế:
Vớ dụ:
Điều kiện:
Vậy phương trỡnh cú nghiệm
II. BẤT PHƯƠNG TRèNH LễGARIT
1. Phương trỡnh cơ bản:
a. , Điều kiện
b. , Điều kiện
Vớ dụ 1: Giải bất phương trỡnh:
Điều kiện
Kết hợp với điều kiện, bất phương trỡnh cú nghiệm:
Vớ dụ 2: Giải bất phương trỡnh:
+ Điều kiện
+
+ Kết hợp với điều kiện, bất phương trỡnh cú nghiệm:
+ Hay
2. Phương phỏp: Biến đổi bất phương trỡnh về dạng cựng cơ số:
a. , Điều kiện
b. , Điều kiện
Vớ dụ 1: Giải bất phương trỡnh:
HD: + Điều kiện:
+
+ Kết hợp với điều kiện, bất phương trỡnh cú tập nghiệm:
Vớ dụ 2: Giải bất phương trỡnh:
HD: + Điều kiện:
+ Lỳc đú:
+ Kết hợp với điều kiện, bất phương trỡnh cú nghiệm là :
Vớ dụ 3: Giải bất phương trỡnh:
HD: + Điều kiện:
+ Lỳc đú:
+ Kết hợp với điều kiện, bất phương trỡnh cú nghiệm là : ... đỏy ABCD là hỡnh vuụng cạnh a. Mặt bờn (SAB) là tam giỏc đều và S
D
a
H
C
A
B
vuụng gúc với đỏy. Gọi H là trung điểm của AB
a) Chứng minh rằng: SH (ABCD)
b) Tớnh thể tớch hỡnh chúp S.ABCD
HD: a) * Ta cú: mp(SAB) (ABCD)
* (SAB) (ABCD) = AB; * SH (SAB)
* SH AB ( là đường cao của SAB đều)
Suy ra: SH (ABCD) (đpcm)
b) * Tớnh: VS.ABCD = Bh = SABCD.SH
* Tớnh: SABCD = a2 * Tớnh: SH = (vỡ SAB đều cạnh a)
ĐS: VS.ABCD =
7a
6a
5a
N
M
H
P
C
B
A
60
°
S
Bài 4: Cho hỡnh chúp S.ABC cú AB = 5a, BC = 6a, CA = 7a. Cỏc mặt bờn (SAB), (SBC), (SCA) tạo với đỏy
một gúc 600. Tớnh thể tớch của khối chúp đú.
HD: * Hạ SH (ABC) và kẻ HM AB, HNBC, HP AC
* Gúc tạo bởi mặt bờn (SAB) với đỏy (ABC) là = = 600
* Ta cú: Cỏc vuụng SMH, SNH, SPH bằng nhau (vỡ cú chung 1 cạnh
gúc vuụng và 1 gúc nhọn bằng 600)
* Suy ra: HM = HN = HP = r là bỏn kớnh đường trũn nội tiếp ABC
* Tớnh: VS.ABC = Bh = SABC .SH
* Tớnh: SABC =
= (cụng thức Hờ-rụng)
* Tớnh: p = Suy ra: SABC =
* Tớnh SH: Trong SMH tại H, ta cú: tan600 = SH = MH. tan600
* Tớnh MH: Theo cụng thức SABC = p.r = p.MH MH = = Suy ra: SH =
ĐS: VS.ABC =
Bài 5: Cho hỡnh chúp tam giỏc đều S.ABC cú cạnh AB bằng a. Cỏc cạnh bờn SA, SB, SC tạo với đỏy một
gúc 600. Gọi D là giao điểm của SA với mặt phẳng qua BC và vuụng gúc với SA.
a) Tớnh tỉ số thể tớch của hai khối chúp S.DBC và S.ABC
60
°
E
D
a
H
C
B
A
S
b) Tớnh thể tớch của khối chúp S.DBC
HD: a) Hạ SH (ABC) H là trọng tõm của ABC đều cạnh a
Gọi E là trung điểm của BC
* Gúc tạo bởi cạnh bờn SA với đỏy (ABC) là = = 600
* Tớnh:
* Tớnh SD: SD = SA – AD
* Tớnh SA: SA = 2AH (vỡ SAH là nửa tam giỏc đều)
và AH = AE mà AE = vỡ ABC đều cạnh a.
Suy ra: SA =
* Tớnh AD: AD = ( vỡ ADE là nửa tam giỏc đều). Suy ra: AD =
* Suy ra: SD = . ĐS:
b) Cỏch 1: * Tớnh VS.ABC = Bh = SABC.SH * Tớnh: SABC = (vỡ ABC đều cạnh a)
* Tớnh SH: Trong SAH tại H, ta cú: sin600 = SH = SA.sin600 = a. Suy ra: VS.ABC =
* Từ . Suy ra: VS.DBC =
Cỏch 2: * Tớnh: VS.DBC = Bh = SDBC.SD * Tớnh: SDBC = DE.BC
* Tớnh DE: Trong ADE tại D, ta cú: sin600 = DE = AE.sin600 =. Suy ra: SDBC =
Bài 6: Cho khối chúp tứ giỏc đều SABCD. Một mặt phẳng qua A, B và trung điểm M của SC . Tớnh tỉ số thể tớch của hai phần khối chúp bị phõn chia bởi mặt phẳng đú.
Giải.
Kẻ MN // CD (N thỡ hỡnh thang ABMN là thiết diện của khối chúp khi cắt bởi mặt phẳng (ABM).
+
+
Mà VSABMN = VSANB + VSBMN = . Suy ra VABMN.ABCD =
Do đú :
III, Bài tập về nhà
Bài 1. Cho hỡnh chúp S.ABC cú đỏy là tam giỏc ABC vuụng tại B, đường thẳng SA vuụng gúc với mặt phẳng (ABC). Biết AB = a, và .
Tớnh thể tớch khối chúp S.ABC theo a.
Gọi I là trung điểm của cạnh SC, tớnh độ dài đoạn thẳng BI theo a.
(TN-THPT 2008 lần 2)
Bài 2. Cho hỡnh chúp S.ABC cú mặt bờn SBC là tam giỏc đều cạnh a, cạnh bờn SA vuụng gúc với mặt đỏy. Biết , tớnh thể tớch của khối chúp S.ABC theo a. (TN-THPT – 2009)
Buổi 18:Thể tích khối lăng trụ
I, Mục tiêu:
- Nắm được CT tính thể tích khối lăng trụ V = B.h ( B là diện tớch của đỏy )
-Biết cách tính thể tích khối lăng trụ, biết phân chia một khối đa diện.
II, Luyện tập
C'
B'
A'
C
B
A
Bài 1: Cho hỡnh lăng trụ đứng tam giỏc ABC.A’B’C’ cú tất cả cỏc cạnh đều bằng a
a) Tớnh thể tớch của khối lăng trụ
b) Tớnh thể tớch khối tứ diện A’BB’C
HD: a) * Đỏy A’B’C’ là đều cạnh a . AA’ là đường cao
* Tất cả cỏc cạnh đều bằng a
* = Bh = .AA’
* Tớnh: = (A’B’C’ là đều cạnh a) và AA’ = a
ĐS: = b) = ĐS:
( khối lăng trụ đứng cú tất cả cỏc cạnh bằng nhau được chia thành 3 tứ diện bằng nhau)
60
°
30
°
C'
B'
A'
C
B
A
Bài 2: Cho lăng trụ đứng ABC.A’B’C’, đỏy ABC là tam giỏc vuụng tại A, AC = a, = 600, đường chộo BC’
của mặt bờn (BCC’B’) hợp với mặt bờn (ACC’A’) một gúc 300.
a) Tớnh độ dài cạnh AC’ b) Tớnh thể tớch lăng trụ
HD: a) * Xỏc định là gúc giữa cạnh BC’ và mp(ACC’A’)
+ CM: BA ( ACC’A’)
BA AC (vỡ ABC vuụng tại A)
BA AA’ (ABC.A’B’C’ lăng trụ đứng)
+ = = 300 * Tớnh AC’: Trong BAC’ tại A (vỡ BA AC’)
tan300 = AC’ = = AB
* Tớnh AB: Trong ABC tại A, ta cú: tan600 =
AB = AC. tan600 = a (vỡ AC = a). ĐS: AC’ = 3a
b) = Bh = .CC’ * Tớnh: = AB.AC = .a.a =
* Tớnh CC’: Trong ACC’ tại C, ta cú: CC’2 = AC’2 – AC2 = 8a2 CC’ =
ĐS: = a3
Bài 3: Cho lăng trụ tam giỏc ABC.A’B’C’ cú đỏy ABC là một tam giỏc đều cạnh a và điểm A’ cỏch đều cỏc
điểm A, B, C. Cạnh bờn AA’ tạo với mp đỏy một gúc 600. Tớnh thể tớch của lăng trụ.
HD: * Kẻ A’H (ABC)
* A’ cỏch đều cỏc điểm A, B, C nờn H là trọng tõm của ABC đều cạnh a
a
60
°
N
H
C'
B'
A'
C
B
A
* Gúc giữa cạnh AA’ và mp(ABC) là = = 600
* Tớnh: = Bh = .A’H
* Tớnh: = (Vỡ ABC đều cạnh a)
* Tớnh A’H: Trong AA’H tại H, ta cú:
tan600 = A’H = AH. tan600 = AN. = a
ĐS: =
Bài 4: Cho lăng trụ đứng ABC.A’B’C’, đỏy ABC là tam giỏc vuụng tại A, AC = a, BC = 2a và AA’ = 3a.
2a
3a
a
C'
B'
A'
C
B
A
Tớnh thể tớch của lăng trụ
HD: * Đường cao lăng trụ là AA’ = 3a
* Tớnh: = Bh = .AA’
* Tớnh: = AB.AC (biết AC = a)
* Tớnh AB: Trong ABC tại A, ta cú:
AB2 = BC2 – AC2 = 4a2 – a2 = 3a2
ĐS: =
Bài 5: Cho hỡnh lăng trụ tứ giỏc đều ABCD.A’B’C’D’ cú chiều cao bằng h và gúc của hai đường chộo của hai mặt bờn kề nhau phỏt xuất từ một đỉnh là . Tớnh thể tớch của lăng trụ.
Giải
Gọi x là cạnh của đỏy, ta cú B’D’ = x
.Vậy V = x2.h =
Bài 6: Đỏy của lăng trụ đứng tam giỏc ABC.A’B’C’ là tam giỏc đều . Mặt (A’BC) tạo với đỏy một gúc 300 và diện tớch tam giỏc A’BC bằng 8. Tớnh thể tớch khối lăng trụ.
Giải.
Giả sử BI = x
Ta cú
A’A = AI.tan 300 =
Vậy VABC.A’B’C’ = CI.AI.A’A = x3
Mà SA’BC = BI.A’I = x.2x = 8.Do đú VABC.A’B’C’ = 8
III, Bài tập về nhà.
Bài 1. Cho hỡnh lăng trụ tam giỏc ABC.A’B’C’ cú , gúc giữa đường thẳng BB’ và mặt phẳng (ABC) bằng ; tam giỏc ABC vuụng tại C và . Hỡnh chiếu vuụng gúc của điểm B’ lờn mặt phẳng (ABC) trựng với trọng tõm của tam giỏc ABC. Tớnh thể tớch khối tứ diện A’ABC theo a.
Bài 2. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là mụ̣t tam giác vuụng tại A, , . Đường chéo BC’ của mặt bờn (BB’C’C) tạo với mặt phẳng (AA’C’C) mụ̣t góc . Tớnh thể tớch khối lăng trụ ABC.A’B’C’ theo a.
Buổi 19: Diện tích và thể tích các khối tròn xoay
I, Mục tiêu:
- Nắm chắc và sử dụng thành thạo các công thức:
1. Diện tớch xung quanh hỡnh trụ: Sxq = ( R: bỏn kớnh đỏy, l : độ dài đường sinh)
2. Thể tớch khối trụ: V = ( h : độ dài đường cao )
3. Diện tớch xung quanh hỡnh nún: Sxq =
4. Thể tớch khối nún: V =
5. Diện tớch mặt cầu: S =
6. Thể tớch khối cầu: V =
II, Luyện tập
Bài 1: Trong khụng gian cho tam giỏc vuụng OAB tại O cú OA = 4, OB = 3. Khi quay tam giỏc vuụng OAB quanh cạnh gúc vuụng OA thỡ đường gấp khỳc OAB tạo thành một hỡnh nún trũn xoay. a) Tớnh diện tớch xung quanh và diện tớch toàn phần của hỡnh nún
3
4
A
B
O
Tớnh thể tớch của khối nún
HD: a) * Sxq = Rl = .OB.AB = 15
Tớnh: AB = 5 (AOB tại O)
* Stp = Sxq + Sđỏy = 15 + 9 = 24
b) V = = = = 12
2a
A
B
S
O
Bài 2: Một hỡnh nún cú thiết diện qua trục là một tam giỏc đều cạnh 2a.
Tớnh diện tớch xung quanh và diện tớch toàn phần của hỡnh nún
Tớnh thể tớch của khối nún
HD: a) * Sxq = Rl = .OB.SB = 2a2
* Stp = Sxq + Sđỏy = 2a2 + a2 = 23a2
b) V = = =
Tớnh: SO = (vỡ SO là đường cao của SAB đều cạnh 2a)
Bài 3: Một hỡnh nún cú chiều cao bằng a và thiết diện qua trục là tam giỏc vuụng.
Tớnh diện tớch xung quanh và diện tớch toàn phần của hỡnh nún
45
S
B
A
O
Tớnh thể tớch của khối nún
HD: a) * Thiết diện qua trục là tam giỏc vuụng cõn tại S nờn = = 450
* Sxq = Rl = .OA.SA = a2
Tớnh: SA = a; OA = a (SOA tại O)
* Stp = Sxq + Sđỏy = a2 + a2 = (1 + ) a2
b) V = = =
Bài 4: Một hỡnh trụ cú bỏn kớnh đỏy bằng R và thiết diện qua trục là một hỡnh vuụng.
A
B
O
O'
A'
B'
l
h
Tớnh diện tớch xung quanh và diện tớch toàn phần của hỡnh trụ
Tớnh thể tớch của khối trụ
HD: a) * Sxq = 2Rl = 2.OA.AA’ = 2.R.2R = 4R2
* OA =R; AA’ = 2R
* Stp = Sxq + 2Sđỏy = 4R2 + R2 = 5R2
b) * V = = =
Bài 5: Một hỡnh trụ cú bỏn kớnh đỏy r = 5cm và khoảng cỏch giữa hai đỏy bằng 7cm.
Tớnh diện tớch xung quanh và diện tớch toàn phần của hỡnh trụ
Tớnh thể tớch của khối trụ
h
r
l
B'
A'
O'
I
O
B
A
Cắt khối trụ bởi một mặt phẳng song song với trục và cỏch trụ 3cm. Hóy tớnh diện tớch của thiết diện được tạo nờn
HD: a) * Sxq = 2Rl = 2.OA.AA’ = 2.5.7 = 70(cm2)
* OA = 5cm; AA’ = 7cm
* Stp = Sxq + 2Sđỏy = 70 + 50 = 120(cm2)
b) * V = = = .52.7 = 175(cm3)
c) * Gọi I là trung điểm của AB OI = 3cm
* = AB.AA’ = 8.7 = 56 (cm2) (hỡnh chữ nhật)
* AA’ = 7 * Tớnh: AB = 2AI = 2.4 = 8
* Tớnh: AI = 4(cm) (OAI tại I)
Bài 6: Một hỡnh trụ cú bỏn kớnh r và chiều cao h = r
Tớnh diện tớch xung quanh và diện tớch toàn phần của hỡnh trụ
Tớnh thể tớch của khối trụ tạo nờn bởi hỡnh trụ đó cho
Cho hai điểm A và B lần lượt nằm trờn hai đường trũn đỏy sao cho gúc giữa đường thẳng AB và trục của hỡnh trụ bằng 300. Tớnh khoảng cỏch giữa đường thẳng AB và trục của hỡnh trụ
r
3
H
A
B
O
O'
A'
r
HD: a) * Sxq = 2Rl = 2.OA.AA’ = 2.r. r = 2r2
* Stp = Sxq + 2Sđỏy = 2r2 + 2r2 = 2 (r2
b) * V = = =
c) * OO’//AA’ = 300
* Kẻ O’H A’B O’H là khoảng cỏch giữa đường thẳng AB
và trục OO’ của hỡnh trụ
* Tớnh: O’H = (vỡ BA’O’ đều cạnh r)
* C/m: BA’O’ đều cạnh r * Tớnh: A’B = A’O’ = BO’ = r
* Tớnh: A’B = r (AA’B tại A’)
Cỏch khỏc: * Tớnh O’H = = (A’O’H tại H)
* Tớnh: A’H = = * Tớnh: A’B = r (AA’B tại A’)
Bài 7: Cho tứ diện ABCD cú DA = 5a và vuụng gúc với mp(ABC), ABC vuụng tại B và
AB = 3a, BC = 4a. a) Xỏc định mặt cầu đi qua 4 điểm A, B, C, D
b) Tớnh bỏn kớnh của mặt cầu núi trờn. Tớnh diện tớch và thể tớch của mặt cầu
HD: a) * Gọi O là trung điểm của CD.
* Chứng minh: OA = OB = OC = OD;
* Chứng minh: DAC vuụng tại A OA = OC = OD = CD
(T/c: Trong tam giỏc vuụng trung tuyến thuộc cạnh huyền bằng nửa cạnh ấy)
O
D
C
B
A
* Chứng minh: DBC vuụng tại B OB = CD
* OA = OB = OC = OD = CD A, B, C, D thuộc mặt cầu S(O; )
b) * Bỏn kớnh R = = =
=
* S = ; * V = R3 =
Bài 8: Cho hỡnh chúp tứ giỏc đều S.ABCD cú tất cả cỏc cạnh đều bằng a.
Xỏc định mặt cầu đi qua 5 điểm A, B, C, D, S
Tớnh bỏn kớnh của mặt cầu núi trờn. Tớnh diện tớch và thể tớch của mặt cầu
HD: a) Gọi O là tõm hỡnh vuụng (đỏy). Chứng minh: OA = OB = OC = OD = OS
b, R = OA = ; S = 2a2; V =
III, Bài tập về nhà.
Bài 1: Cắt hỡnh nún đỉnh S bởi mặt phẳng đi qua trục ta được một tam giỏc vuụng cõn cú cạnh huyền bằng
Tớnh diện tớch xung quanh và diện tớch toàn phần của hỡnh nún
Tớnh thể tớch của khối nún
Cho dõy cung BC của đường trũn đỏy hỡnh nún sao cho mặt phẳng (SBC) tạo với mặt phẳng chứa đỏy hỡnh nún một gúc 600. Tớnh diện tớch tam giỏc SBC
Bài 2: Cho một hỡnh trụ cú hai đỏy là hai đường trũn tõm O và O’, bỏn kớnh R, chiều cao hỡnh trụ là R.
Tớnh diện tớch xung quanh và diện tớch toàn phần của hỡnh trụ
Tớnh thể tớch của khối trụ
Bài 3: Cho hỡnh chúp S. ABCD cú đỏy ABCD là hớnh vuụng cạnh bằng a. SA = 2a và vuụng gúc với mp(ABCD).
a) Xỏc định mặt cầu đi qua 5 điểm A, B, C, D, S
b) Tớnh bỏn kớnh của mặt cầu núi trờn. Tớnh diện tớch và thể tớch của mặt cầu
Tài liệu đính kèm:
 on thi tot nghiep toan lop 12.doc
on thi tot nghiep toan lop 12.doc





